基于二维切削理论的绞刀刀臂载荷分析＊

杨桢毅 朱汉华 范世东 裴 炯

（武汉理工大学能源与动力工程学院1） 武汉 430063） （兰州理工大学能源与动力工程学院2） 兰州 730050）

0 引 言

在疏浚工程中，绞吸式挖泥船是应用较为广泛的一种船型.绞刀是绞吸式挖泥船的核心挖掘部件，通过绞刀的旋转切割水下土层，使泥沙与水相混合，形成一定浓度的泥水混合体（泥浆），泥浆通过泥泵的真空抽吸作用，经输泥管道输送到排泥场，完成疏浚挖泥过程.

绞刀与所切削的土壤之间存在着较大的挖掘力作用，如何有效地计算出它们的相互作用力对于挖掘机具的设计和降低工程成本起着重要的作用.国内外设计挖泥船绞刀时通常是依靠经验公式确定绞刀尺寸，用波兰斯斐拉公式计算绞刀的切削力.大量试验证明，绞刀所需要的功率的大小由绞刀尺寸、土壤的坚实度、切削泥层厚度和绞刀横移速度等决定.设计者在设计绞刀时力求用小切削力获得高生产率，从而可减少功率消耗.

水饱和沙的二维切削理论分别由van Os［1］，Verruijt［2］，Miedema［3－4］以及van Leussen和van Os［5］提出并发展，如今已经被广泛运用.当泥土的力学参数、挖掘部件的几何结构以及有效挖掘功率为已知时，就能用二维切削理论预测产量.本文基于Miedema的二维切削理论，利用MATLAB求解了绞刀刀臂所受的作用力，用ANSYS对切削过程中进行了挖掘过程和受力分析.

1 绞刀切削力学分析

1.1 切削形式分析

在工程挖泥船上，绞刀都是采用空间曲面的三维螺旋绞刀，这种螺旋型刀臂的结构与形状使整个切削过程都能够连续地进行，有效避免瞬时冲击力的产生.绞刀刀臂的倾斜程度一般用螺旋升角，即绞刀刀臂与大环平面的夹角来描述，由于该角度为面与面的空间夹角，难以直接测量，因此引入了包角，见图1.图中λ为包角.假设刀臂的包角为λ，高度为h，则单位包角的高度值为h／λ.当绞刀高度一定时，包角就决定了刀臂的螺旋上升程度.

选取刀臂的包角为75°，切削土层的转角为90°的状态进行分析［6］.

做一系列垂至于绞刀轴的截面去剖切绞刀，它们相对绞刀轴心转过的角度形成不同的刀臂截面.螺旋绞刀在做横移切削时，同一刀臂上不同的位置切削状态不同，刀臂不是同时进入或离开切削层，而是先进先出或后进后出；也可能会是其中某段刀臂参与切削.所以切削分析中需确定绞刀所处位置以及每个参与切削刀臂的切削范围.

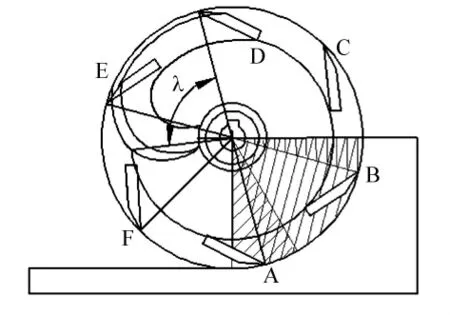
图1 包角为75°，绞刀处于15°时刻的切削范围扇形图

当刀刃开始切削瞬间的切向速度与横移速度方向一直时，垂直于速度方向且通过轴心的平面设为基准面.如图1所示，A刀臂基准面处在15°时刻的切削范围扇形示意图.

A刀臂切削范围为15°～90°，把15°～90°之间各个作用力累加起来，就是A刀臂的计算结果.由图1可知，该切削范围内还有前一刀臂B、后一刀臂F在土层中切削，计算方法与A刀臂相同.对于6刀臂绞刀的整个切削过程来讲，切削的周期为60°，则可列出如表1临界时刻的切削范围分布情况.

表1 临界时刻的切削范围

由分析可知，绞刀头的包角越大，即绞刀头的扭曲程度越大，切削功率的变化越趋于平缓，对绞刀的运行越有利.

1.2 受力分析

绞刀在切削的过程中，存在粘性力等较小的作用力，为研究方便，忽略不计.引入二维切削理论［7］，刀臂进行切削时，简化后的受力见图2和图3.

图2，3中，N2为作用在刀片上的法向力；S2为泥土与刀片的摩擦力N2tanδ引起的剪切力；A2为泥土和刀片之间的粘性剪切力；W2为作用在刀片上的水下压力引起的力；W3为刀片后面的水下压力引起的力；W1为在剪切区域由水压力引起的作用力；N1为作用在剪切面上的法向力；S1为内摩擦力引起的剪切力；c为沙土的内聚力引起的作用力；G为沙土的重力；T为泥土加速度引起的惯性力；W4为水阻力.

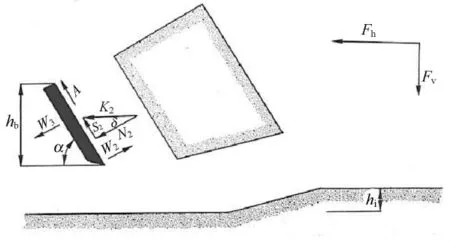
图2 作用在刀片上的力

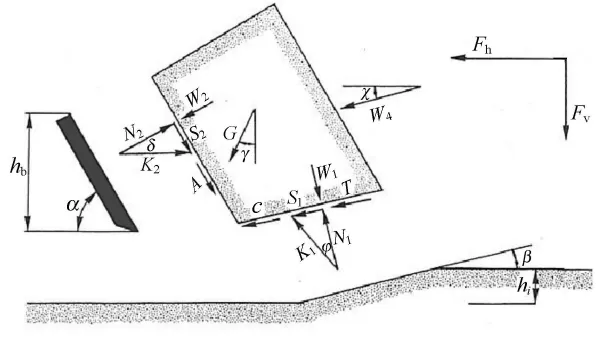
图3 作用在切削层上的力

建立水平和垂直2个方向上的力的平衡方程，计算得到K1和K2

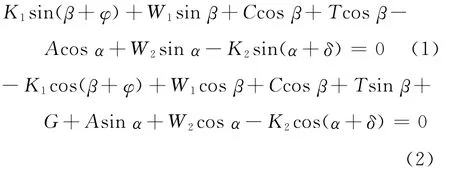
为了简化，将K2分解为K21和K22，即K2＝K21＋K22，

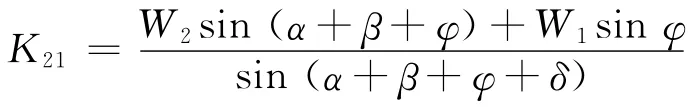
设定绞刀的横移为0.4m／s，转速较低，不至于产生气蚀现象，所以只考虑绞刀在非气蚀情况下所受载荷的情况，则切削力和法向力为

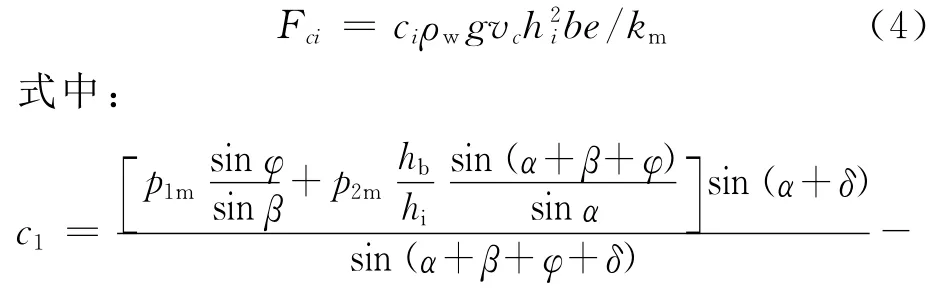
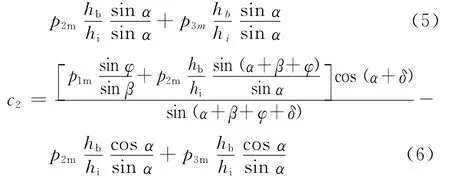
上述公式中ρw为水的密度；g为重力加速度.而无因次系数c1、c2的值，与内摩擦角φ、泥土表面摩擦角δ、切削角α以及刀片高度与层厚度的比例hb／hi有关，需要根据具体情况来确定.

2 切削计算实例与结果

2.1 计算参数

设刀臂包角为λ，高度为h，用若干间隔为h／λ、方向垂直于绞刀轴的截面去切割绞刀后，绞刀被切割成λ等分，如图1可近似认为每相连等分的切削状态相差1°，刀臂最顶端到最底端切削状态将刚好相差λ°，这个计算过程比较繁琐但很有规律.绞刀6个刀臂均布在绞刀圆周上，即每隔T／6，绞刀的切削情况就会一样，所以只需研究T／6内的情况，也就是要研究0°～60°时刻内的情况.

绞刀参数：绞刀的刀圈内径d，2.10m；绞刀高度h，1.65m；转速n，240r／min；横移速度v，0.4m／s；刀臂数Z，6；刀臂有效宽度b，0.250m；切削角a，40°；表面摩擦角δ，20°；内摩擦角φ，37.5°；绞刀功率，100kW；弹性模量，175GPa；泊松比，0.25.

土质特征：土质，细砂；密实度，中密；渗透系数Ki，6×10－5m／s；孔隙度ni，45%；弹性模量，1.3GPa；泊松比，0.35.

由以上数据插值后得c1＝0.301，c2＝0.249.

以上参数参考天津宏大船舶有限公司所设计的2 000m3／h绞吸式挖泥船为例，对其工作过程所受力进行估算.

2.2 计算结果

在MATLAB中编程，输入转速、包角、横移速度、半径、刀臂高度、和无因次系数c1和c2的值等，就可以计算得到75°包角内每一度受力分布，以及在一个周期内作用在单个刀臂上的瞬时切削力和平均切削力.

如图4所示，当刀臂为75°包角时，随着转角增大，刀臂的受力分布也增加.由于刀臂呈现扭曲状，使得切削力的瞬时值没有太大的波动，即有效地保证了绞刀头所受冲击的相对平稳，这对绞刀本身和绞刀架都是有利的，如图5所示.以速度0.4m／s横移时，计算得到切削力的切向力Fh＝3 629.1N，法向力Fv＝3 002.2N.

依据绞刀头受力的经验公式［8］，结合以上绞刀的技术参数，可知在绞刀头上形成的转矩为

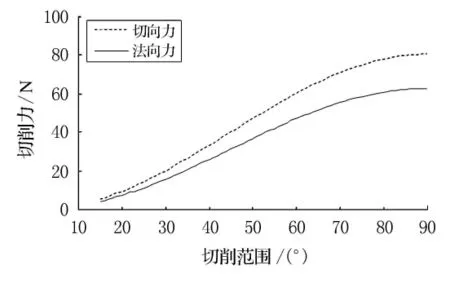
图4 刀臂75°包角时切削相差1°受力分布状态

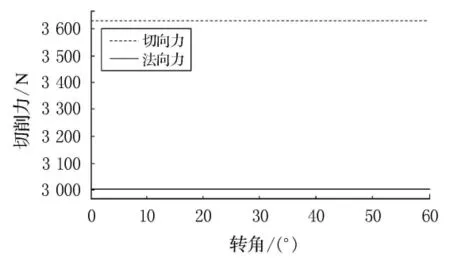
图5 一个周期内的瞬时切削力

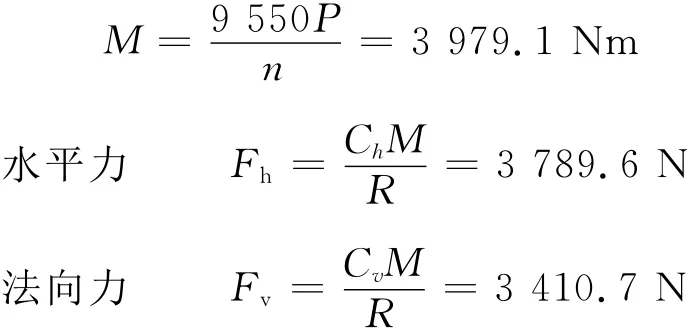
由以上计算结果可知，绞刀的受力都存在的偏差大小为

对切削过程建模及并进行分析，如图6，图7.可以比较具体的表示出土壤在绞刀以240r／min的转速进行切削时的位移及应力分布.

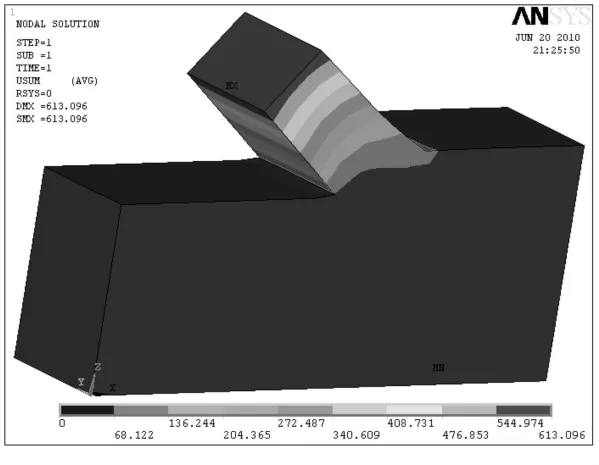
图6 土壤位移云图

图7 土壤应力云图

3 结束语

根据切削理论得到的水平力和法向力，利用MATLAB求解了绞刀刀臂所受的力，并利用ANSYS对绞刀切削过程进行了分析，说明Miedema等人为了预测作用在绞刀上的力，运用二维平板切削理论以简化计算是可行的，根据切削理论的计算结果均处在较小的偏差范围内.本文工作为下一步应用ANSYS软件求解三维切削力作了初步探索.

［1］van Os A G.Behaviour of soil when excavated underwater［C］／／International Course Modern Dredging，Hague，The Netherlands，1977：135－141.

［2］VERRUIJT A.Offshore soil mechanics［D］.Delft：Delft University of Technology，1994.

［3］ MIEDEMA S A.Calculation of the cutting forces when cutting water saturated sand［D］.Delft：Delft University of Technology，1987.

［4］MIEDEMA S A.On the cutting forces in saturated sand of a seagoing cutting suction dredger［C］／／Proc.WODCON XII，Orlando，Florida，USA，April 1989.

［5］van Os A G.LEUSSEN W.Basic jesearch on cutting forces in saturated sand［J］.Journal of Geotechnical Engineering，1987，113（12）：151－159.

［6］张德新.基于二维切削理论的绞刀切削载荷计算及绞刀应力状态的ANSYS分析［D］.南京：河海大学，2007.

［7］MIEDEMA S A.The cutting mechanisms of water saturated sand at small and large cutting angles［J］.Delft University of Technology，Mechanical ＆Dredging Engineering，Mekelweg 2，2628CD Delft，The Netherlands，2004（1）：1－13.

［8］潘英杰.基于二维切削理论的绞吸式挖泥船绞刀头载荷分析［J］.船海工程，2009，38（2）：35－39.