基于等值线搜索带的地磁匹配算法＊

谭 斌 林春生 傅 慷

（海军工程大学兵器工程系1） 武汉 430033） （海军91458部队2） 三亚 572021）

0 引 言

地磁匹配方法是地磁匹配导航系统的核心部分.在磁场传感器性能、基准数字地磁图和载体运动轨迹确定的情况下，匹配算法的效率和精度直接影响着导航系统的性能，是地磁导航系统中的关键环节.目前，关于地磁匹配算法主要有两类：相关度量技术和递推滤波技术［1－2］.其中，相关度量技术的特点是原理简单，可以断续使用，在航行载体需要导航定位时，即开即用，对初始误差要求低，导航不存在误差积累，具有较高的匹配精度和捕获概率，是一种较方便灵活的匹配方式.递推滤波技术的特点是，需要载体在较长一段时间内连续递推滤波导航定位，对初始误差要求较高，滤波的各种误差统计模型不易获取，而且滤波的发散也不易控制.目前应用较多的还主要为卡尔曼滤波技术［3－9］.在这两类算法中，现有的研究表明，基于相关度量技术的地磁匹配方法可以获得比滤波方法更高的导航精度，更适合作为巡航导弹、水面舰船、水中潜器等载体的主要或辅助导航方法［10］.本文主要针对相关度量技术中的TREOCM算法存在的计算量大、实时性较差的问题，提出了一种基于等值线搜索带的改进算法，减少了匹配搜索时间，提高了匹配算法的实时性.

1 搜索策略

在TERCOM算法中，通过在地磁基准图中一个与最大容许导航误差相适应的正方形格网化搜索区域内，以每一个网格点为起始点对测量航迹进行逐格平移，进行遍历搜索计算，从而得到与地磁测量序列最相似的匹配序列.虽然这种算法原理简单，易于实现，且具有较高的匹配精度和捕获概率，但是这种算法的计算量相当大，并且有大量的计算都消耗在了非匹配点的计算上.当搜索区域较大或匹配长度较长时，导航系统的实时性将难以保证，因此需要对算法中的搜索策略进行改进，提高算法效率.

图1所示为对4条不同飞行航迹，经过100次地磁匹配仿真试验后，各条匹配航迹起始点在地磁基准图中的位置分布.从匹配结果中，发现最终得到的最佳匹配航迹的起始点与真实航迹的起始点，都位于地磁基准图上航迹起始点地磁场测量值对应的等值线附近.

由此，可以将搜索区域进一步缩小到起始点地磁测量值对应地磁场等值线附近区域，再通过对测量航迹进行平移来生成待匹配航迹，从而有效减少算法的计算量.如图2所示，真实航迹起始点Pr所在地磁场等值线C1，与C1邻近的2条等值线C2，C3，在以惯导指示航迹起始点Pi为中心，惯导系统±3σ误差为半径，形成的矩形搜索区域内，划分出了一条以L1，L2为边界的搜索带.根据以往匹配结果的推论，可以假定最佳匹配航迹的起始点一定在上述搜索带内，因此，以该搜索带内的每个网格点为起始点，将惯导指示航迹进行平移生成待匹配航迹，对这些待匹配航迹上的地磁特征值序列与实测地磁特征值序列进行相关计算，从而得到最佳匹配航.需要注意的是，等值线的疏密程度不宜取得过密，以免算法收敛到局部最佳匹配航迹，导致出现误匹配.这种基于等值线搜索带的匹配算法，缩小了待匹配序列搜索区域，减小了计算量，提高了算法效率.

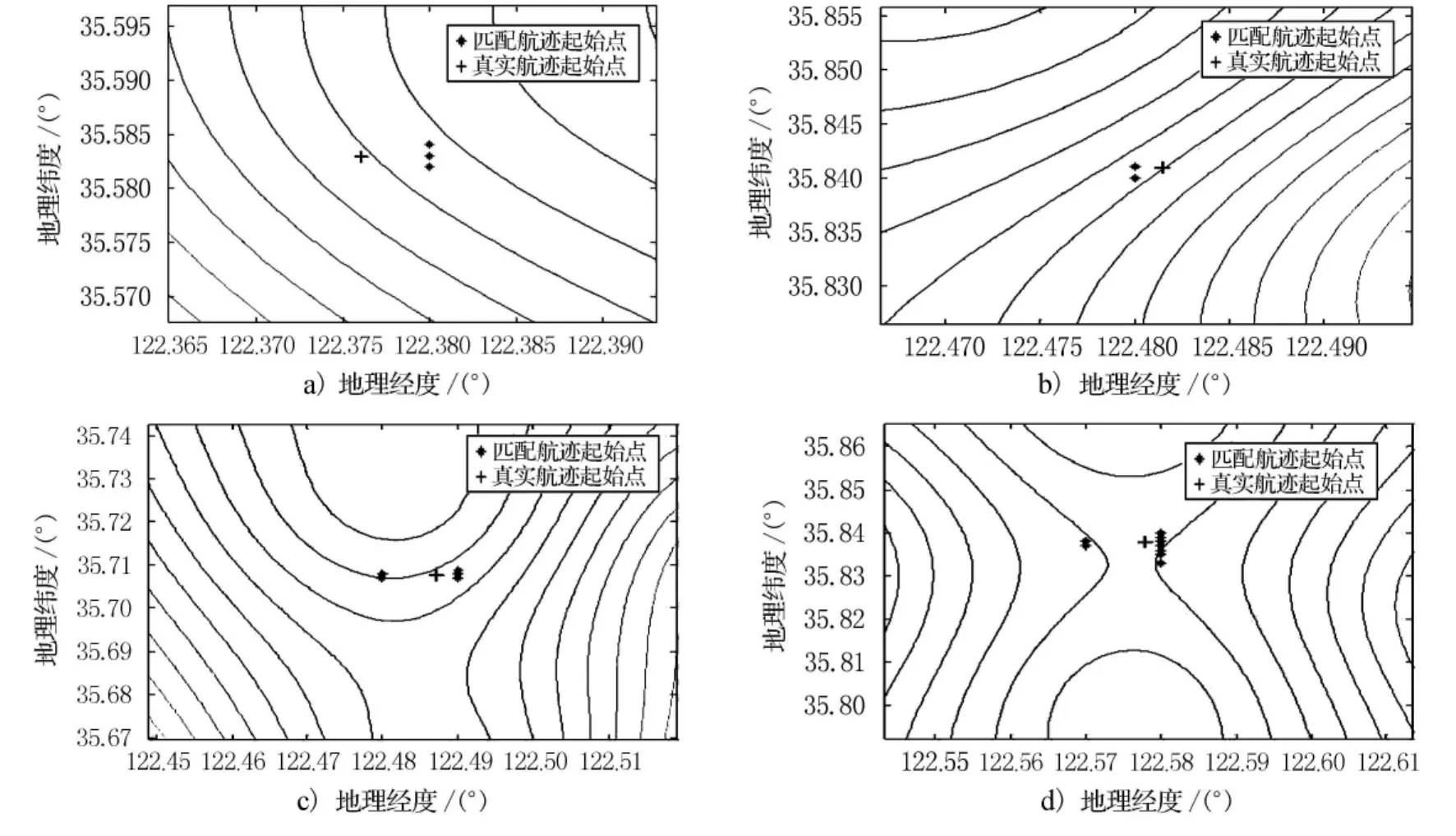
图1 匹配航迹起始点分布

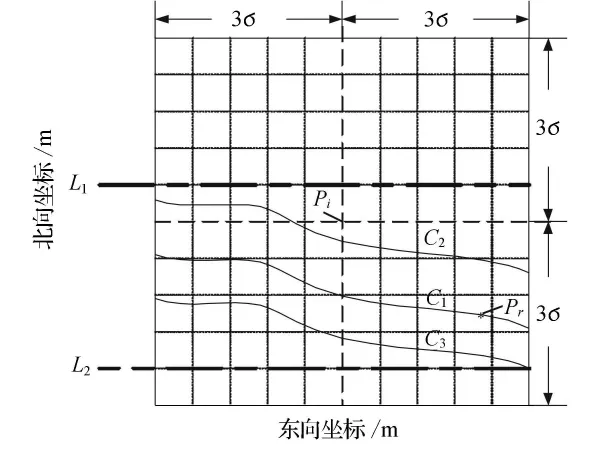
图2 等值线搜索带示意图

2 匹配算法实现步骤

匹配算法的具体实现步骤如下：

步骤1 建立地磁实时测量数据序列.

步骤2 在数字基准图上，建立以惯导系统估算的测量序列初始位置为中心，惯导系统的 误差幅度为大小的网格化搜索区域；根据与测量序列起始点地磁场测量值所对应的地磁场等值线邻近的两条地磁场等值线，将搜索区域缩小至上述两条地磁场等值线之间的带状网格化区域.

步骤3 设惯导系统输出的位置序列为SN＝｛（xk，yk），k＝1，2，…，N｝，将惯导输出位置序列在带状搜索区域中进行平移变换得到搜索位置序列SST（xk＋τx，yk＋τy），τx，τy分别为东向和北向偏移，再根据搜索位置序列在基准图中进行重采样，获得地磁基准序列.

步骤4 根据MSD算法计算每个基准序列与实时测量序列的均方差，取其中最小值对应的网格位置为最佳匹配位置.

步骤5 根据最佳匹配位置对导航系统进行修正.

匹配过程的数学描述为

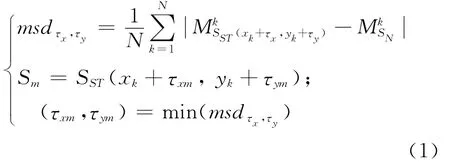
3 仿真试验

为了验证基于等值线搜索带匹配算法的性能，进行了匹配仿真试验.仿真试验中，利用经过处理的北海某海区航空地磁异常场测量数据，建立了该区域的100m×100m网格化地磁异常场基准图.设定载体初始位置误差为1 000m，磁传感器的采样频率为20Hz，采样数据长度L＝20m，并在真实地磁测量值上加上方差为10的零均值高斯白噪声.以地磁场总强度异常为匹配特征量，分别采用TERCOM算法和基于等值线搜索带的匹配算法，对图3中所示航迹进行了100次的蒙特卡洛仿真匹配试验.

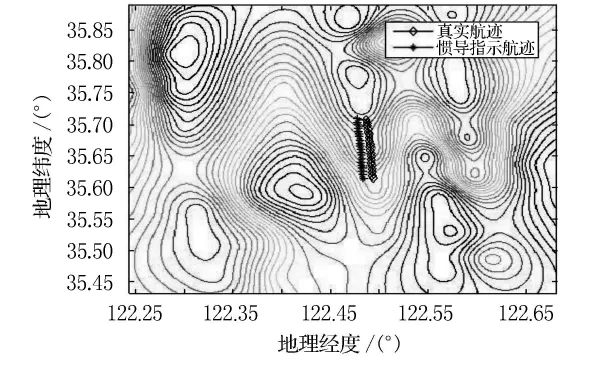
图3 仿真航迹

为了评价匹配效果，采用纬度误差、经度误差以及位置误差均方根以及匹配概率4个指标来衡量匹配结果，各指标定义如下

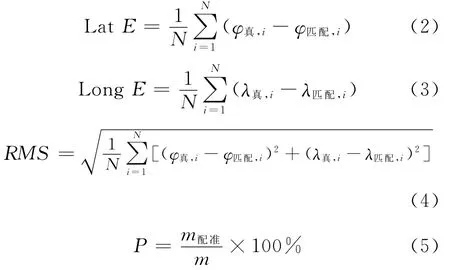
式中：Lat E为匹配值与真实值之间的纬度误差均值，m；LongE为匹配值与真实值之间的经度误差均值，m；RMS为匹配值与真实值之间位置误差的均方根值，m；N 为测量点的个数；λ真，i，φ真，i（i＝1，2，…，N）分别表示真实航迹的第i个点的经纬度值；λ匹配，i，φ匹配，i（i＝1，2，…，N）分别表示匹配航迹的第i个点的经纬度值；P为匹配概率；m和m配准分别为仿真匹配次数和配准次数.在计算匹配概率过程中，当匹配航迹RMS位置误差小于100m时，认为匹配结果为有效匹配，反之，则为误匹配，将有效匹配的次数与仿真匹配试验次数的比值作为匹配概率.仿真试验结果分析见表1.

表1给出了基于TERCOM和基于等值线搜索带的两种算法，在100次匹配仿真中，匹配航迹与真实航迹之间的位置误差均方根均值以及匹配时间均值.从仿真试验结果中可以看出，基于等值线搜索带的匹配算法与基于TERCOM算法的匹配误差均值相当，而基于等值线搜索带的匹配算法有效降低了匹配时间，提高了匹配算法的实时性.

表1 算法的匹配性能分析

4 结束语

本文研究并提出了一种基于地磁场等值线搜索带的地磁匹配算法，通过将搜索区域缩小到航迹起始点地磁测量值对应的地磁场等值线附近区域，再在搜索区内沿网格对测量航迹进行平移来生成待匹配航迹.与传统TERCOM算法相比，该算法能够在保证匹配精度的前提下，有效减少计算量，提高了匹配算法的效率和实时性.Jersey：John Wiley ＆Sons Inc.，2001.

［1］杨云涛，石志勇，关贞珍.地磁场在导航定位系统中的应用［J］.中国惯性技术学报，2007，15（6）：686－692.

［2］肖胜红，边少锋.利用不充分磁场信息导航的新方法［J］.武汉理工大学学报：交通科学与工程版，2010，34（5）：908－911.

［3］GREWAL M S，ANDREWS A P.Kalman filtering theory and practice using matlab［M］.Hoboken，New

［4］RICE H，KELMENSON S，MENDELSOHN L.Geo－Physical navigation technologies and applications［C］／／Position Location and Navigation Symposium，April 26－29，2004：618－624.

［5］GAO Changsheng，JING Wuxing，ZHANG Yan，et al.Autonomous navigation of low－earth－orbit satellites using magnetic measurements by unscented Kalman filter［J］.Chinese Space Science and Technology，2006（1）：27－32.

［6］JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［J］.IEEE Review，2004，92（3）：401－422.

［7］傅 军，张晓锋，方晓旻，等.水下组合导航UKF／PF自适应滤波算法［J］.武汉理工大学学报：交通科学与工程版，2008，32（6）：1106－1109.

［8］王宇飞.基于地磁环境仿真系统的卫星导航算法研究［D］.哈尔滨：哈尔滨工业大学，2006.

［9］杨功流，李士心，姜朝宇.地磁辅助惯性导航系统的数据融合算法［J］.中国惯性技术学报，2007，15（1）：47－50.

［10］周 军，葛致磊，施桂国，等.地磁导航发展与关键技术［J］.宇航学报，2008，29（5）：1467－1471.