基于ECC的移动自组网成员控制方案＊

耿永军 陈红军 郑明辉

（河南城建学院计算机科学与工程系1） 平顶山 467036） （湖北民族学院信息学院2） 恩施 445000）

移动自组网有着无线通信、无网络基础架构、动态成员变化和异构设备的独特特性，传统网络和移动自组网之间的关键差别在于后者缺少对整个网络进行集中控制和管理的节点.在传统网络，中央管理节点负责定义整个网络的安全服务和策略，并可提前分发密钥给所有参与通信的网络用户.但在移动自组网中设置中央节点会导致单点实效的问题.Kong等［1］提出RSA门限数字签名来解决成员控制问题，但这些方法没有提供可验证的的特性，以至于不能抵抗内部恶意节点的攻击，并且该方案要求在自组网形成时有可信的第三方初始化整个群组.Zhou和 Hass［2－3］首先提出在自组网形成时将证书颁发中心（CA）分布在整个网络以避免单点失效，移动自组网中的每个成员拥有一个秘密份额，当一个新成员要加入网络时，网中多个旧成员通过门限数字签名的方法给新加入成员颁发成员证书，但是Zhou和Hass没有将自组网中节点的计算能力、电源、带宽和存储资源限制考虑进去.椭圆曲线密码体制（ECC）在效率上优于前者，更适合于内存和处理能力有限的设备.杜春来［4］和王刚［5］采用 ECC实现移动自组网的组密钥协商和成员身份认证，但没有解决内外恶意节点的攻击和新成员加入问题.本文基于Pederson分布式密钥产生方案［6－7］采用 ECC提出一个分布式密钥产生协议，该方案高效且能抵制内外恶意节点的攻击，并采用门限数字签名方案给出一个安全的移动自组网的成员控制方案.最后，通过方案的性能和安全性分析得出结论，该成员控制策略非常适合于资源受限的移动自组网.

1 基于ECC的分布式密钥产生协议

该密钥产生协议基于改进的Pederson方案，方案去除需要中央控制节点选择秘密多项式和分发成员秘密份额，并采用ECC体制提高运算和通信效率.让A 表示群成员集合，A＝｛u0，u1，…，un－1｝.p是个大素数，y2＝x3＋ax＋b（mod p）表示一个椭圆曲线方程，其中a，b∈Zp＊，4a3＋27b2≠0（mod p），G表示椭圆曲线方程上的一基点G∈E（GF（p））.大素数q是基于有限域Fp的椭圆曲线点构成的群的元素个数，称为该群的阶，q＝＃E（GF（p）），p＋1－2p＜q＜p＋1＋2H（）是一个安全的单向散列函数，IDi表示群成员Ui的公共成员身份.每个群成员有一个成员身份IDi，群组密钥产生的步骤如下.

步骤1 每个群组成员ui（0≤i≤n－1）随机选择一个t－1次秘密多项式：

fi（x）＝ai，0＋ai，1x＋ … ＋ai，t－1xt－1mod q ui（0≤i≤n－1）计算fi（IDj）（0≤j≤n－1）和ai，kG（0≤k≤t－1）.

每个ui（ui∈A）通过秘密信道分别发送fi（IDj）给uj（0≤j≤n－1）and（j≠i）.ui（ui∈A）广播公共信息ai，kG（0≤k≤t－1）给群组中成员.

步骤2 群组成员uj（uj∈A）从ui（0≤i≤n－1）and（i≠j）收到所有的fi（IDj）和ai，kG（0≤k≤t－1）后，uj（0≤j≤n－1）分别验证下列等式：

步骤3 假如上面的验证真正确，uj通过计算下式得到他的秘密份额sj.

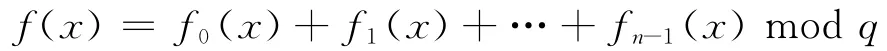
成员秘密份额可表示为si＝f（IDi）.群秘密s＝f（0）分布存放在群中所有成员，群公钥为

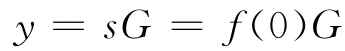
任何群中t个成员联合通过Shamir的秘密共享Lagrange插值多项式［6］可恢复出秘密s.

2 移动自组网成员加入方案及分析

2.1 方案描述

成员控制方案能确保那些满足成员控制规则的用户得到合法成员证书，从而成为合法群组成员，成员控制规则是群组安全策略的一部分.在本文提出基于ECC门限机制的成员控制方案，根据前面产生的群密钥和公钥进行签名和验证.其中群密钥s被群组中所有成员通过（t，n）门限机制共享，每个群组成员拥有自己的秘密份额.任一个群组成员通过自己的秘密份额对消息产生部分签名，群组签名合成者至少需要t个成员的部分签名生成对消息的群组签名.通过这种方法，t个群组成员可代表群组生成新加入成员的群组成员证书.假如群组中成员已经根据基于ECC的Pederson分布式密钥产生协议拥有一份秘密份额，群组成员控制方案如下.

2.1.1 群组成员颁发新成员证书

步骤1 新成员请求加入群组 新成员un通过发送JOIN＿REQ消息给群中成员.un用自己的私钥签发自己的请求加入消息M，并将其公钥一同发给群组中成员.

步骤2 颁发新成员证书的群组成员交换参数 接到JOIN＿REQ请求消息的群组成员用请求者的公钥验证请求消息的签名是否有效.假如群组中的成员同意新成员un的入网请求，他就用自己秘密份额的对请求消息M部分签名回复un.用V＝｛v1，v2，…，vt｝表示给新成员颁发证书的集合，l≥t.

每个进行群组签名的群成员vi（i＝1，2，…，l）随机选取ki（ki∈），且计算

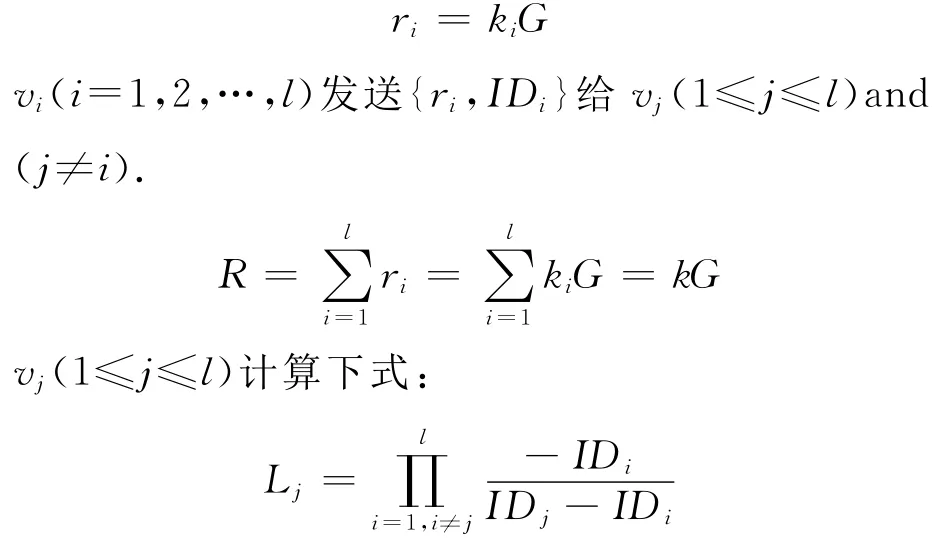
假如vi想要计算k＝，他必须知道ki（1≤i≤l）的值，要想从ri（1≤i≤l）得到ki（1≤i≤l）必须先解决椭圆曲线离散对数问题.所以，k值被群组中成员vi（i＝1，2，…，l）共享，但任何参加签名的单个群成员不知k值.

步骤3 新成员证书的颁发 每个参加群签名的群组成员vi（i＝1，2，…，l）计算下面2个方程，本文用｛R｝x表示椭圆曲线上一点R 的x轴坐标.（本文中，表示Lagrange相关系数）：

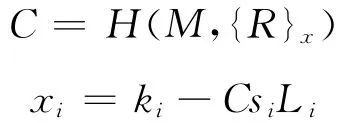
vi（i＝1，2，…，l）发送｛C，xi｝给新成员作为部分签名.

新成员接收到不少于t个部分签名后，他将部分签名｛C，X｝合成为对请求消息M 的有效群签名.

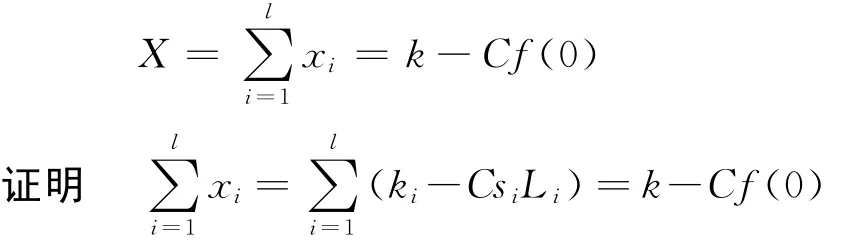
步骤4 新成员证书的验证 任何群成员可通过群组公钥y验证签名｛C，X｝.验证者计算下列方程

验证者验证下列等式是否成立.

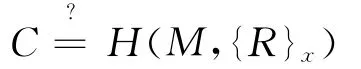
假如这个验证成立，意味着新成员un得到一个合法的群成员证书.但是一个新成员得到成员证书是不够的，新成员也应有自己的秘密份额将来为其他要加入的新成员进行部分签名，下面为新成员得到成员秘密份额的过程.

2.1.2 新成员秘密份额的获得

步骤1 假如un成为了一个合法的群成员，他需要有自己的秘密份额sn使自己参加将来新成员加入的裁决协议，每个参加群组签名者vi（i＝1，2，…，l）计算下列等式：

步骤2 vi（i＝1，2，…，l）秘密发送Si给新成员.

步骤3 新成员un根据Lagrange插值多项式计算下列方程得到他的秘密份额.

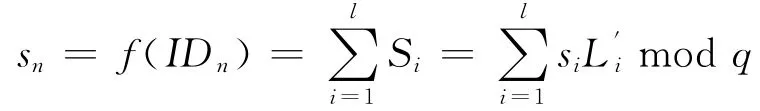
这里存在一个安全问题，L′i是公开的，un能通过Si求出si.文献［5］中提出了shuffling技术解决该问题.在一个有shuffling技术的方案中，参加签名的群组中任两成员交换一个随机值nonce.ID值大的群成员将把这个nonce当做正值，而另一方将其作为负值.每个参加签名的成员至少有t－1个这样的nonce.在vi（i＝1，2，…，t）发给新成员部分秘密份额前，他先求出他已知l－1个nonce的和and Si，然后发送一个封装的＝si＋ ∑（nonce）部分秘密份额给un.

2.2 安全性分析

下面证明本文提出的改进方案满足抵抗合谋攻击、伪造攻击.该改进方案的安全性基于下面两个困难性假设：大整数分解问题和单向hash函数的不可逆性.先证明该方案的正确性，然后证明其满足的安全性质.

方案的正确性证明

定理1 该成员控制方案能安全实现新成员的证书颁发，任何群成员可通过群组公钥y验证签名｛C，X｝，只要满足R＝XG＋Cy，且C＝H（M，｛R｝x）成立，证书便是合法的.

证明 XG＋Cy＝R－Cf（0）G＋Cf（0）G＝R

方案满足的安全性：

1）该成员控制方案满足门限机制，且能抵制伪造攻击 假如至少有t个群组成员同意新成员加入群组，新成员可以得到有效的群成员证书.另一方面，少于t个群组成员同意其加入，新成员则不能得到有效证书.基于上面的密钥产生协议，可知群组成员秘密份额si＝f（IDi）（1≤i≤t）.通过Lagrange插值多项式，不少于t个群组成员可用自己秘密份额恢复群组秘密f（0）.少于t个群组成员合作根据shamir的秘密共享方案则不能，且攻击者要从公共信息中得到秘密成员份额，由于椭圆曲线的离散对数难题世人尚没有解决.所以该攻击也不成立.

2）该成员控制方案可抵制内部成员的攻击

假如新成员被接受为合法的群组成员，由于采用了shuffling技术实现部分秘密份额的分发，使得新成员得到自己的秘密份额而得不到其他群组成员的秘密份额.由于随机nonce对新成员是个秘密，由其封装的发给新成员后，新成员想通过得到si是困难的，但通过式snew＝f（IDnew）可得到自己的秘密成员份额.

从图1很容易验证采用Shuffling技术后，un可得到同样的sn值，且新成员不能得到其他群组成员的秘密份额.

图1 Shuffling技术实现示意图

2.3 仿真性能分析

该方案是基于椭圆曲线密码体制，其用加操作替代乘操作.方案中的q只需要160bits就可获得RSA 1024bits或DSA 512bits的安全强度.由于同样的安全强度和更短的密钥长度，方案实施所需要的内存和网络带宽缩小了.下面给出该方案采用PBC开发库软件的编程实现，具体运行环境如下：Celeron 1.4GHz＋760MRAM＋ Windows XP＋VC8.0.方案仿真中椭圆曲线参数选取为

有限域P：1514632635174592562243141915 959568687003144559398080982579809

参数a：791107111

参数b：1077150514903

基点 G：（644644487，16367426894330）

群组密钥s：357321394324624475504410370 0527078272835564256634324140533

群组公钥y：（30092692644613787357405824 5124271641822522762978019682442886，526316 386840250105483025593133809754064234349343 842898534047）

群组成员数设为4，门限值设为3，由于3个成员进行部分签名是在分布式环境同时进行，部分签名开销只计单个成员为38ms，新成员合成签名的时间开销为0ms，新成员验证签名时间开销为47ms.

3 结束语

本文基于Pederson分布式密钥产生方案采用ECC提出一个分布式密钥产生协议，该方案高效且采用shuffling技术能抵制内外恶意节点的攻击，并利用门限数字签名方案给出一个安全的移动自组网的成员控制方案.最后，通过方案的性能和安全性分析得出结论，该成员控制策略非常适合于资源受限的移动自组网.满足MANETs的高效要求，也克服现有基于大整数分解和离散对数的无可信中心的门限数字签名没有把移动节点计算能力、电源、带宽和存储资源限制条件考虑进去的缺陷.

［1］KONG J，ZERFOS P，LUO H，et al.Providing robust and ubiquitous security support for mobile adhoc networks［C］／／IEEE ICNP，2001：98－102.

［2］ZHOU L，HAAS.Securing ad hoc networks［J］.IEEE Network Magazine，1999（11）：112－117.

［3］李成霞.一种ECC快速数字签名技术的硬件实现［J］.武汉理工大学学报，2009，31（19）：156－159.

［4］杜春来.在椭圆曲线域中基于身份认证的移动ad hoc密钥管理框架［J］.通信学报，2007，28（12）：53－60.

［5］王 刚.移动自组网中安全高效的组密钥管理方案［J］.计算机研究与发展，2010，47（5）：911－921.

［6］PEDERSEN T，A threshold cryptosystem without a trusted party［C］／／Advances in Cryptology－Eurocrypt＇91.LNCS 547，Springer－Verlag，1991：128－132.

［7］SHAMIR A.How to share a secret［J］.Communications of the ACM，1979，24（11）：612－613.