基于图像处理的外螺纹三维模型重构
2012-09-25姜立军陈学东李哲林
万 鹏, 姜立军, 陈学东, 李哲林
(1. 华南理工大学机械与汽车工程学院,广东 广州 510640;2. 华南理工大学设计学院,广东 广州 510640;3.惠州新协和表面处理制品厂,广东 惠州 516000)
基于图像处理的外螺纹三维模型重构
万 鹏1, 姜立军2, 陈学东3, 李哲林2
(1. 华南理工大学机械与汽车工程学院,广东 广州 510640;2. 华南理工大学设计学院,广东 广州 510640;3.惠州新协和表面处理制品厂,广东 惠州 516000)
提出了一种基于多角度序列图像特征实现外螺纹的三维模型重建的方法。首先在旋转平台上采集多角度序列螺纹件图像,然后对每帧图像进行特征点提取,将序列图像的特征点进行三维变换和插值,最终生成三维模型。实验结果表明,此算法能精确高精度地实现外螺纹三维模型重构。
图像处理;螺纹件;特征点;三维模型重构
目前,利用计算机图像处理技术,实现了对螺纹中径、螺距、牙型角三个重要参数的在线测量[1-2]和对螺纹缺陷进行检测[3],均是一种基于平面轮廓或区域的检测方法,以上方法只利用了某个平面轮廓或区域的信息进行检测,没有反映真实的三维立体信息。
在三维模型重建研究中,一般有以下几种:第一,利用三维建模软件构建三维模型,如 3D Max、Maya等。杜忠友等人采用计算机仿真三维螺纹车削成形的方法,实现了三维螺纹的建模[4]。缺点在于:需要充分地掌握场景数据;对不规则物体的建模真实感不高等。第二,利用仪器设备重建三维模型,如三维扫描仪、激光器等。此方法应用广泛,使用便捷。Julio Molleda等人利用激光三角法,实现了对轧制品的三维模型测量[5]。缺点在于:设备较为昂贵,不适合较大物体的三维模型重建。第三,利用图像序列重建三维模型。建模过程自动化,建模成本低,具有广泛的应用前景。
本文提出一种基于计算机图像处理技术,结合三维图形变换,重建螺纹件三维模型的算法,实现了外螺纹件的三维模型重构,为三维测量提供三维模型数据。首先介绍了序列图像采集的方法,然后分析了图像处理流程和三维重构算法,并通过实验验证了算法的通用性,最后对此重构算法进行了总结,提出了影响重构效果的因素和需要进一步研究的内容。
1 系统组成及实验步骤
将螺纹件固定在旋转实验台上,通过电机带动实验台旋转,实现多角度序列图像采集,如图1所示。系统各组成部分参数为:计算机为研华工控机(PC-610MB-F),摄像头为单色 CD(1394 DMK 21BF04),镜头型号为COMPUTAR MLM 3X MP、后焦距为 20.4 mm,光照采用 Ose BT50*50红色背光源,旋转试验台直径为240mm、转速为 4转/分钟,摄像头到旋转中心的距离为260 mm。实验采用的螺纹件如图2所示。

图1 螺纹件图像采集系统

图2 试验用螺纹件
具体实验步骤如下:
1) 调整光源与照相机的高度,将螺纹件固定在旋转实验台中心;
2) 通过电机匀速转运实验平台,每旋转18°自动采集一帧螺纹件图像,共采集10帧图像;
3) 对采集的图像进行预处理并提取螺纹的波峰波谷特征点;
4) 特征点三维化及表面插值,生成螺纹件的三维模型。
2 螺纹图像处理和三维模型重构
2.1 图像处理流程
通过CCD相机获取螺纹图像,运用图像处理技术提取特征点,计算出螺纹轮廓上的波峰和波谷点。图像处理流程如图3所示。采集的螺纹原始图像如图4(a)所示;要降低因光照环境和螺纹材质、表面等原因引起的噪声,又要保持螺纹的边缘特征,采用边缘保持滤波器对原始图像进行增强处理,处理之后的效果图如图4(b)所示;螺纹轮廓的提取,主要是对螺纹边缘进行提取,本文采用Canny算法来提取螺纹轮廓,Canny算子产生的边界较细、定位精度高、单一边缘好,Canny边缘提取算法最适合用于螺纹图像[6],提取螺纹轮廓如图 4(c)所示;本文采用文献[7]中的方法,实现亚像素特征提取,提取波峰波谷特征点图像如图4(d)所示。

图3 提取螺纹特征点流程

图4 螺纹图像处理
2.2 特征点归类
为了对提取的螺纹波峰波谷特征点进行标注,将螺纹图像的横轴作为X轴,纵轴作为Y轴,建立二维坐标系,如图5所示。为了使各帧图像间波峰特征点与波峰特征点、波谷特征点与波谷特征点分别相对应,对图中的螺牙上波峰波谷点进行归类。按照左侧波峰、左侧波谷、右侧波峰、右侧波谷进行归类。建立4个数组来存储这4类数据,以图5所示的图像为例,其中特征点的坐标(Xi,Yi)按表1所示进行管理。

图5 螺纹特征点和坐标系标注
2.3 螺纹三维模型重建2.3.1 校正坐标轴中心
螺纹件在旋转的过程中可能会发生轴线的移动,为了使每张图像的坐标轴中心保持一致,把坐标轴中心平移到螺纹件图像中心。将原始数据的X坐标减去每张图像的中心偏移量Δx,为获得偏移量Δx,可以分别取左右两边螺纹各点的X轴坐标平均值X1和X2,再取X1和X2的平均值作为X轴的偏移量,如图6所示。

表1 部分螺纹特征点

图6 校正坐标轴
2.3.2 三维坐标点转换
将每帧图像中的二维坐标点转换成对应的三维坐标点。某点绕坐标原点逆时针旋转θ角的变换为

可知坐标点(X,Y)绕坐标原点逆时针旋转θ角后的新坐标点(X*,Y*)为

将二维图像置于三维空间XZ平面中,点(x,y)对应于三维图像中的坐标点为(x, 0,y),绕Z轴逆时针旋转θ角后的三维坐标点(X,Y,Z)为

图形在旋转过程中,只改变空间位置,其形状大小是不变的。本实验中每次旋转角度为18°,第i帧图像的旋转角度为18° *(i-1),如图7所示。

图7 坐标点转换
2.3.3 坐标点插值
为了使重建的三维模型达到较好的效果,在相邻两张图片之间插值两次,即对应的波峰或波谷之间分别插值两个点,如图8所示,实心点为原始坐标点,空心点为插值坐标点。由于每张图片间距 18°,故两次插值角度分别为θ1=6°、θ2=12°。

图8 插值示意图
设第1张图片中的坐标点(x1,y1,z1)和第2张图片中的坐标点(x2,y2,z2)之间进行两次插值,插值坐标点分别为(X1,Y1,Z1)和(X2,Y2,Z2),计算公式如下

通过此插值,可以将坐标点数据增加两倍,实现用较少图像快速生成密集的三维点,重构较光滑的螺纹件三维模型。
2.3.4 生成坐标点及序号
将各坐标点按顺序构建三角面片,如图8所示,每个三角面片由相对应的波峰点和波谷点构成。按照自定义的obj数据文件格式生成三维坐标点、插值坐标点以及构成三角面片的坐标点序号,参考格式如下:

利用自主开发的软件打开生成的obj数据文件,三维模型效果图如图9所示。
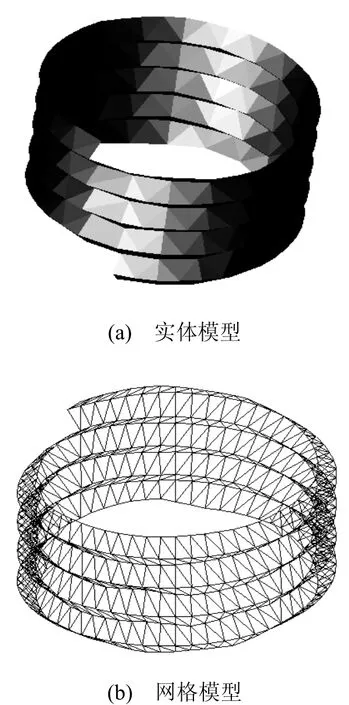
图9 螺纹三维模型
3 实验结果
为了验证三维模型重构算法的通用性,对4个多角度序列的螺纹件图像进行三维模型重构,所生成的三维模型效果如图10所示。
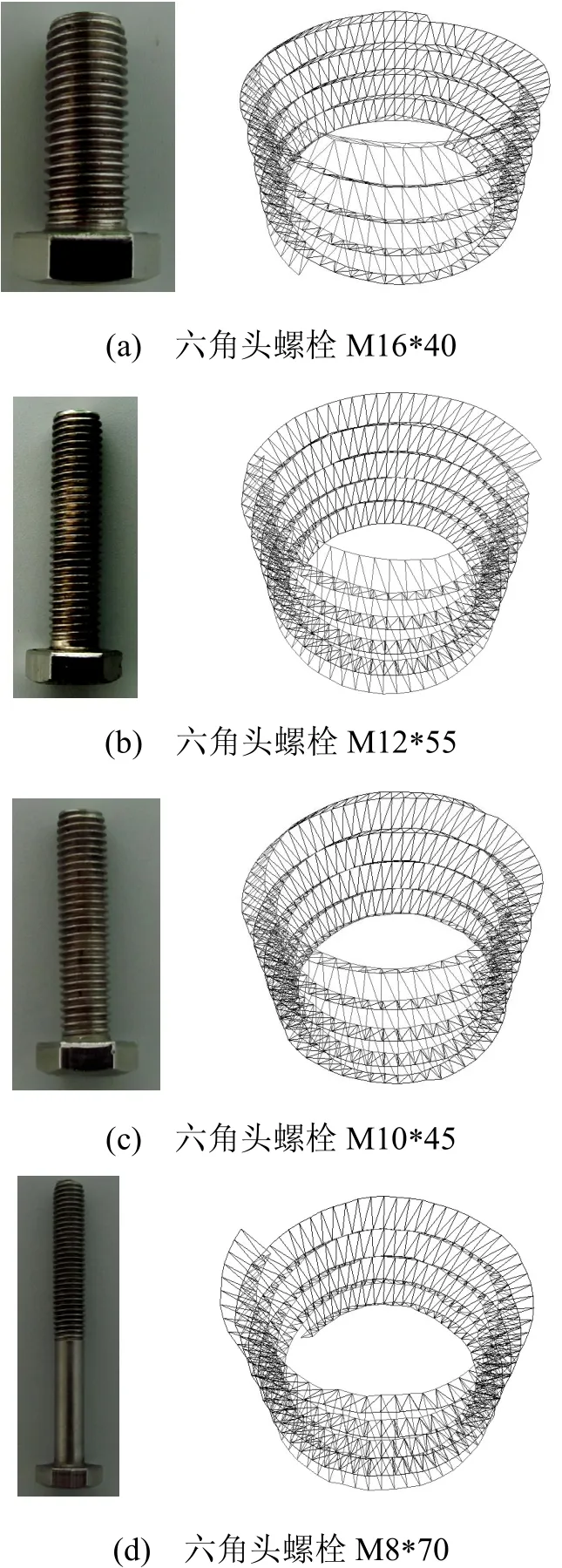
图10 螺纹件三维网格模型
4 结 论
本文简要介绍了对螺纹件的图像处理技术,并利用提取的螺纹特征点重构三维模型,从上面的实验结果中可以看出生成的模型达到较好的效果,能真实地反映螺纹件的表面形状。其中影响模型效果的因素有:螺纹图像特征点的提取精度、旋转角度大小和坐标点插值次数等。目前通过图像处理技术构建了螺纹件三维模型,下一步将研究可以重构的螺纹模型和理论的螺纹模型进行匹配,以达到对螺纹检测的目的。
[1]左建中, 刘 蜂, 张定昭. 机器视觉技术在螺纹检测中的应用[J]. 机械设计与制造, 2006, (4):113-114.
[2]Shen Shaowei, Yan Shuhua, Zhou Chunlei, et al.Research of automatic detection technology of thread parameters based on CCD vision [J]. Semiconductor Optoelectronics, 2007, 28(6):865-869.
[3]周金山, 娄训志, 王 凡, 等. 基于机器视觉的螺纹缺陷检测方法[J]. 湖北工业大学学报, 2010, (4):4-6.
[4]杜忠友, 周 斌. 三维螺纹造型的一种计算机建模方法[J]. CAD CAM, 2006, (11):241-243.
[5]Molleda J, Usamentiaga R, García D F, et al. Shape measurement of steel strips using a laser-based three dimensional reconstruction technique [C]//Industry Applications Society Annual Meeting (IAS), 2010 IEEE, 2010:1-8.
[6] Liu Chenchung, Chen Wenyuan. Screw pitch precision measurement using simple linear regression and image analysis [J]. Applied Mathematics and Computation,2006, 178(2):390-404.
[7]姜立军, 熊志勇, 李哲林. 基于亚像素特征点提取的螺纹检测粗糙聚类算法[J]. 计算机工程与科学,2009, 31(7):43-45, 94.
3D model reconstruction of external thread based on image processing technology
Wan Peng1, Jiang Lijun2, Chen Xuedong3, Li Zhelin2
( 1. School of Mechanical & Automobile Engineering, South China University of Technology, Guangzhou Guangdong 510640, China;2. School of Design , South China University of Technology, Guangzhou Guangdong 510640, China;3. Huizhou New Xiehe Surface Processing Factory, Huizhou Guangdong 516000, China )
This paper proposes a method to realize 3D model reconstruction of thread pieces based on features of multi-angle sequence images. Firstly, multi-angle sequence images of thread pieces are acquired on rotating platform, and feature points are extracted from each image, then 3D transformation and interpolation are conducted to feature points, and finally 3D model is realized. The experiment results show that this algorithm can accurately realize 3D model reconstruction of thread pieces with high presicion.
image processing; thread pieces; feature points; 3D model reconstruction
TP 391
A
1003-0158(2012)01-0068-05
2011-04-16
广东省教育部产学研结合资助项目(2011B090400105)
万 鹏(1987-),男,江西南昌人,硕士研究生,主要研究方向为计算机图学及应用。
