有源滤波器补偿前后负载谐波电流变化的定量分析

，，，

（1.太原理工大学机械工程学院，山西 太原 030024；2.西安交通大学电气工程学院，陕西 西安 710049）

1 引言

有源滤波器作为一种新型的谐波抑制装置，可以动态地补偿谐波，并克服无源滤波器的缺点，具有很大的应用前景［1-4］。近年来，学者们对有源滤波器进行了深入的研究，提出了许多种有源滤波器拓扑和控制策略［5-8］。然而，基于检测负载谐波电流的并联型有源滤波器［5］由于其结构简单，对系统谐波电流开环控制，不存在稳定性问题等优点而在工业场合得到广泛应用。

本文通过建立基于检测负载谐波电流的并联型有源滤波器系统的简化模型，对此模型进行理论分析，定量地给出了补偿前后负载谐波电流的关系，定性并定量地解释了负载谐波电流经过补偿后增大的这一现象。

2 系统结构

并联型有源滤波器结构图如图1所示。图2为指令电流检测控制框图，应用瞬时无功功率理论。图1中iLk（k＝a，b，c）为负载电流，isk为电源电流为指令电流，ick为变流器输出电流，Uk为电源电压为直流侧电压指令，Udc为直流侧电压，Zsa，Zsb，Zsc为电源内阻抗。有源滤波器通过指令检测电路检测负载的谐波电流，与直流侧电压控制电流共同作为指令电流，通过电流闭环控制及PWM控制使有源滤波器输出谐波电流，补偿电源中的谐波电流，最终使电源电流中不含有谐波电流。

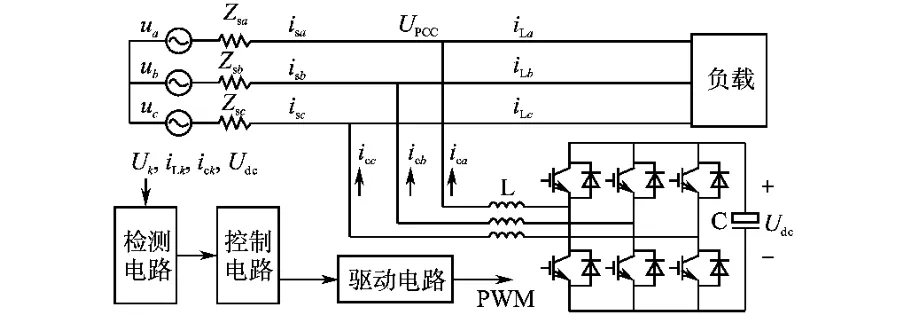
图1 系统结构框图Fig.1 Block diagram of system configuration

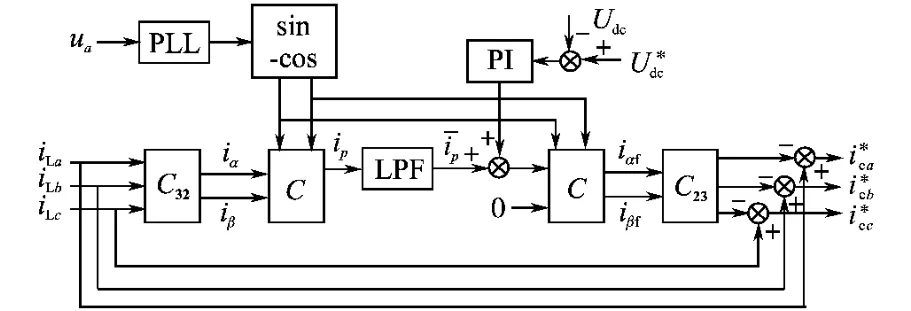
图2 指令电流检测框图Fig.2 Block diagram of reference current calculation

3 简化模型的理论分析

将有源滤波器看作理想的受控电流源ic，并将负载看作带内阻ZL的谐波电流源iL0［9-10］，图1所示的系统模型可以简化为图3。有源滤波器产生与负载谐波电流iL大小相等、方向相反的补偿电流ic，系统电流is就为无畸变的正弦电流，实现滤波功能。按电源电压Us有畸变的一般情况下，只考虑谐波分量，那么对任意次谐波分量等效电路如图4所示。对图4进行电路分析可以得：

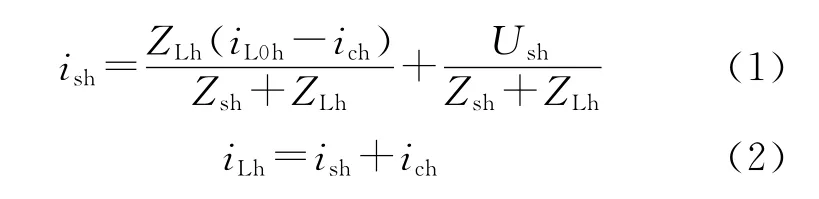
若有源滤波器对负载谐波能完全补偿，那么

将式（3）代入式（1）、式（2）得

图3 系统简化模型Fig.3 System simplified model

图4 系统谐波等效电路Fig.4 System harmonic equivalent circuit

如图5所示，在未加上有源滤波器时，电源电流与负载电流中的谐波分量相等，根据对电路的分析可以得到：

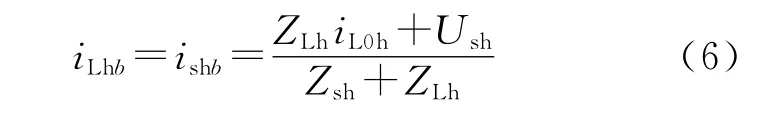
将式（5）代入式（6）可以得：

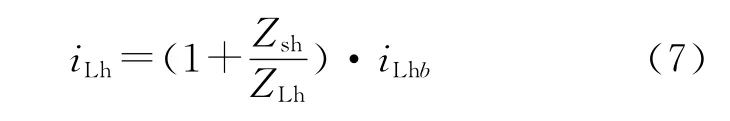
由式（4）、式（7）合并转化为有效值得

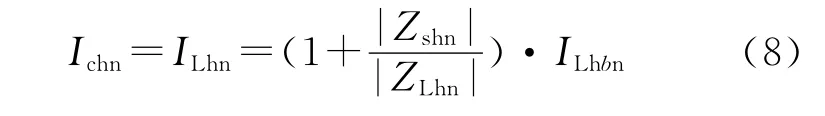
式（7）表示了补偿前后负载谐波电流的关系，可以看出补偿后的负载谐波电流是补偿前的（1＋Zsh／ZLh）倍，显然补偿后的负载谐波电流大于补偿前的负载谐波电流，也就是说负载谐波电流经过补偿后被放大了，放大程度由电源内阻抗Zsh和负载等效内阻抗ZLh的比值决定。电流源型负载的内阻ZLh相对于电源内阻Zsh比较大，ilh略微比iLhb大一些；而电压源型负载的内阻相对于电源内阻Zsh比较小，iLh远大于iLhb，甚至是后者的几倍。所以，并联有源滤波器适用于补偿电流源型负载而不适用于补偿电压源型负载。当负载为不控整流桥带RL负载时，负载电流在补偿前后放大现象在要补偿的负载谐波较小时并不太明显，随着负载谐波容量的增大，这一现象才引起人们的关注和重视；当负载为不控整流桥带RLC或RC负载时，这一现象比较容易被发现。

图5 未加有源滤波器的系统谐波等效电路Fig.5 System harmonic equivalent circuit without APF

4 仿真和实验研究

4.1 仿真及结果分析

采用Matlab／Simulink仿真软件对图1系统进行了仿真。电源线电压为380V，频率为50 Hz；电源内阻抗为Rs＝0.1Ω，Ls＝0.05mH；负载为三相不控整流桥带RCL负载，RL＝1Ω，LL＝0.2mH，CL＝1mF。仿真时间为0.2s，在0.1s时投入有源滤波器来观察有源滤波器投入前后负载谐波电流的变化情况。

图6为系统仿真波形图。图6中的波形由上至下分别为公共连接点电压UPCC，负载电流iL，电源电流is，有源滤波器输出电流ic。在0.1s时投入有源滤波器，有源滤波器输出相应的谐波电流，电源电流is和公共连接点出的电压UPCC得到了有效的补偿，负载电流iL在投入瞬间增大。表1为并联有源滤波器投入前后系统参数的对照表。并联有源滤波器投入后，电源电流is的THD由投入前的21.11减小至3.03，公共连接点电压UPCC的THD由原来的4.79减小至2.67，可见此有源滤波器具有较好的滤波效果。

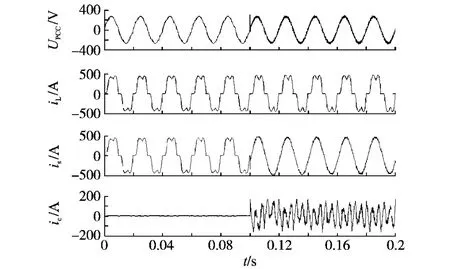
图6 系统仿真波形Fig.6 System simulation waveforms

表1 有源滤波器投入前后系统参数对照表Tab.1 System parameters comparison before and after APF switched on

表1表明有源滤波器投入后，负载电流的有效值由投入前的380.98A增大到393.87A，各次谐波电流也有不同程度的增大。以5次谐波为例，有源滤波器投入后，5次谐波电流由投入前的62.61 A增大到73.49A，即ILh5＝1.17ILhb5。由 Matlab测得｜Zsh5｜＝0.101，｜ZLh5｜＝0.623，代入式（8）可以计算出I′Lh5＝1.16I′Lhb5，计算值与实验测量值基本吻合，证明了式（7）和式（8）的正确性。

4.2 实验及结果分析

本实验在某厂利用50kV·A的并联型有源滤波器进行谐波治理的工业现场进行。电网电压为380V，电网频率为50Hz，负载为整流桥带卷包机负载。图7为并联型有源滤波器未投入时的实验波形。其中图7a为负载电压在5次时FFT分析；图7b为负载电压和负载电流波形；图7c～图7f为负载电流在5次、7次、11次和13次的FFT分析。图8为并联型有源滤波器投入后对应的实验波形。

图7 有源滤波器未投入时实验波形Fig.7 Experiment results when APF switched off

图8 有源滤波器投入后的实验波形Fig.8 Experiment results when APF switched on

由图7和图8对比可以看出，有源滤波器投入后电压总畸变率由原来的7.8%降到了4.5%，其中5次谐波电压从28V降到了16.3V。电压波形得到改善，电能质量明显好转。但5次、7次、11次和13次谐波分别上升了1.6A，1.8A，0.2A，0.2A，负载电流的 THD 也由原来的23.5%上升到26.8%。此实验再现了待治理网络的负载侧电流谐波含量经补偿后会发生增大这一现象，表明了上文理论分析的合理性。

5 结论

本文通过对有源滤波器补偿前后负载电流的定量分析，发现负载谐波电流在有源滤波器投入后放大的程度由电源内阻抗和负载等效阻抗的比值决定的。对负载谐波电流经过有源滤波器补偿后增大这一现象进行了解释。

［1］王兆安，杨君，刘进军.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，1998.

［2］吴竞昌，孙树勤，宋文南，等.电力系统谐波［M］.北京：水利电力出版社，1988.

［3］罗安.电网谐波治理和无功补偿技术及装备［M］.北京：中国电力出版社，2006.

［4］Akagi H.New Treends in Active Filters for Power Conditioning［J］.IEEE Trans.on IA，1996，32（6）：1312－1322.

［5］卓放，杨君，王兆安，等.用于三相四线制系统的有源电力滤波器研究［J］.西安交通大学学报，2000，34（3）：87－90.

［6］Li Dayi，Chen Qiaofu，Jia Zhengchun，etal.A Novel Active Power Filter with Fundamental Magnetic Flux Compensation［J］.IEEE Trans.on Power Deli，2004，19（2）：799－805.

［7］唐欣，罗安，涂春鸣.新型注入式混合有源滤波器的研究［J］.电工技术学报，2004，19（11）：50－55，60.

［8］童立青，钱照明，彭方正.有源滤波器电路拓扑研究综述［J］.电力电子技术，2009，43（10）：2－4.

［9］张轩，刘进军，王兆安.不同负载特性下并联有源滤波器补偿特性的量化分析［C］∥中国电工技术学会电力电子学会第十一届学术年会，杭州，2008：126－130.

［10］王群，姚为正，刘进军，等.谐波源与有源电力滤波器的补偿特性［J］.中国电机工程学报，2001，21（2）：16－20.