永磁直线同步电动机的改进型迭代学习控制

，，

（桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004）

1 引言

永磁直线同步电机采用直接驱动，简化了齿轮、滚珠与螺杆等设备，所以其反应速度更快，灵敏度更高，随动性更好，可以实现超高速运动，另外其在力能指标、定位精度、效率等方面也比其它电机具有更多的优势。但由于采用直接驱动，系统参数摄动、负载扰动以及外部非线性扰动等不确定因素将直接影响直线电机的静动态特性，增加了控制上的难度，特别是在高速的控制过程中，要保证跟踪精度更加不易［1-3］。

迭代学习控制是智能控制的一个分支，它适用于具有重复运动性质的被控对象，它控制能够充分借助历史控制信息构成当前控制输入且不依赖被控系统的详细模型，只根据系统的实际输出信号和期望输出信号的误差来寻找理想的控制信号，使得被控系统的实际输出轨迹在有限的时间区间上沿着整个期望输出的轨迹实现零误差的完全跟踪［4-5］。

传统的迭代学习算法，在实际系统面临新的环境和控制任务时，系统必须重新进行学习，这主要体现在对初始控制输入的选取不含有任何控制经验，这种方法是不符合人类的学习行为，是一种耗时与低效式的学习［6］。针对上述问题，该文提出了一种改进型的迭代学习算法，将迭代控制律看成时间轴与迭代轴的叠加，在迭代轴上引入了一个初始控制量和一个自适应因子，增加了新的信息，初始控制量能够有效地抑制迭代开始时跟踪误差的大幅摆动，然后通过自适应因子调节控制过程中各控制量的比重，有效地实现永磁同步直线电机的跟踪控制。算法的学习速度是衡量该算法是否有应用价值的重要指标，仿真结果表明所提出的算法在学习速度与控制精度方面均比传统迭代算法的控制效果更有效。

2 PMLSM简化数学模型

在忽略铁芯饱和，不计涡流和磁滞损耗，初级上没有阻尼绕组，永磁体也没有阻尼作用，反电动势是正弦的基础上，仅考虑基波分量的永磁同步直线电动机的d－q轴数学模型如下［1］：

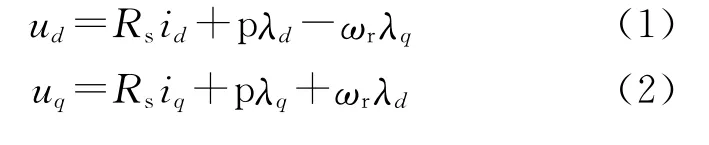
其中

式中：id，iq分别为d，q轴电流；ud，uq分别为d，q轴电压；Ls为电动机的同步电感；Rs为定子相电阻；λPM为定子永磁体产生的励磁磁链；ωr＝πv／τ，v为线速度；p＝d／dt。

电流内环采用励磁分量控制策略，即id＝0，使动子电流矢量与定子永磁体磁场在空间上正交。因此，电磁推力Fe为

机械运动方程：

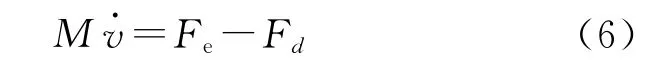
式中：Fe为电磁推力；为动子线速度；τ为极距；M为动子质量；Kf为电磁推力系数；Fd为总阻力，Fd＝Fl＋Fef＋Ff，Fl为负载阻力，Fef为由端部效应引起的推力波动，简化模型为［7］

A为推力波动幅值；ω为以位移为变量的角速度；x为电机运动部分沿运动方向的位移；φ为初始相位；Ff为摩擦力，其模型为［7］

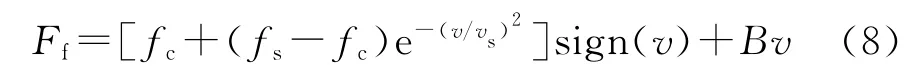
fc为滑动摩擦力；fs为静摩擦力；vs为润滑系数；B为粘滞摩擦系数。

由于直线电机运行时，起主要作用的干扰是粘滞摩擦力，其他非线性因素均看作干扰。根据式（6）、式（8）可得直线电机简化的线性方程为

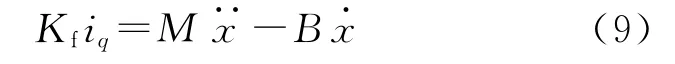
永磁直线同步电机的模型如图1所示。

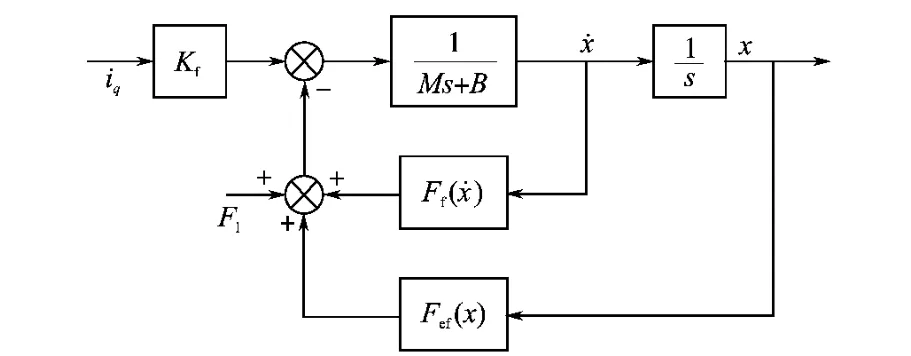
图1 永磁直线同步电机的模型框图Fig.1 Block diagram of the model of a PMLSM

根据上述分析可将位置跟踪系统中PMLSM的状态方程写成如下形式：

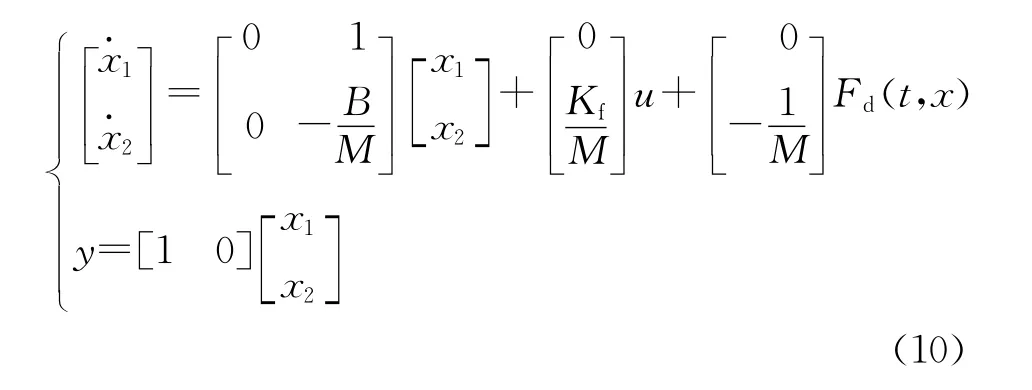
3 改进控制算法的提出

对于一个非线性时变系统：

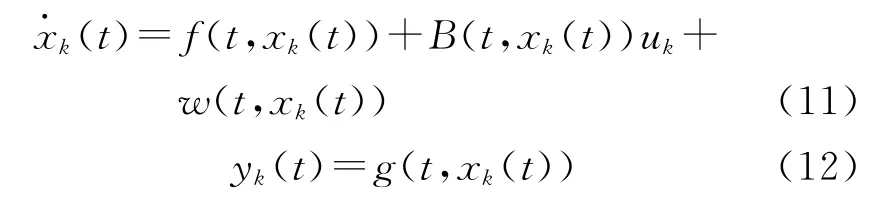
其中，k为迭代次数，u∈Rm，x∈Rn，y∈Rr分别为系统的输入、状态以及输出向量，t∈［0，T］，函数f，B，w，g为非线性函数，且都是Lipschitz连续的，即存在Lipschitz常数kh＞0，h∈｛f，B，w，g｝，使得

对于一个给定的跟踪yd（t），存在唯一一个理想序列ud（t），使得系统的状态和输出为期望值xd（t），yd（t），即满足：

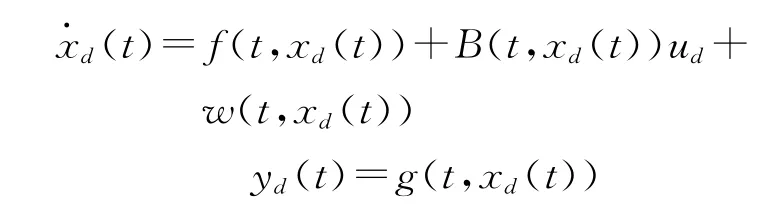
式中：xd（t）为系统的期望状态。

迭代学习控制的任务是通过学习使得控制序列uk（t）（k＝1，2，3，…），尽可能接近理想的控制输入ud（t）。

迭代学习控制是从迭代轴k和时间轴t两个方向同时进行，两轴之间有着紧密联系，其中迭代轴k上过去时刻的控制量值影响着时间轴t上当前的控制量。传统的P型迭代算法在时间轴上仅表现为对误差信息的比例控制，提供的信息相对较少。PD型迭代算法针对P型迭代算法信息量少的缺点，在时间轴t上引入了误差的导数信息，但在迭代轴上未作改变，这样做只能在一定程度上加快系统的跟踪速度，要想实现系统的高速跟踪必须在迭代轴k上也做出相应的改进，增加新的信息。该文提出的改进型迭代算法在迭代轴k上引入一个初始控制量和自适应因子。学习律表达式如下：

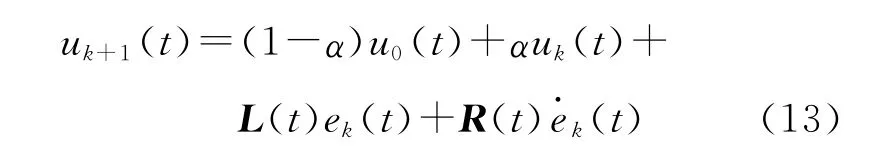
其中，α为自适应因子为一固定系数，其值的大小影响α变化幅度。yk（t））2，从α的定义中可以看出α为一个自适应的变速度因子，其大小与实际输出、期望输出密切相关，在迭代初期由于二者差值较大，所以α的值趋于零，学习律前半部分起主要作用。当系统运行一段时间后，系统趋于稳定时，α值趋近于1，此时学习率主要由后半部分起作用。u0（t）为初始修正项，它可以避免迭代轨迹的大幅摆动，从而加快迭代收敛速度。u0（t）的选择不是一个定值，而是随着实际位置与期望位置差值变化的一个动态值，在本文中u0（t）的值由传统的PD控制器得到，选择PD控制器可以保证系统的抗干扰能力。ek（t）为跟踪误差为跟踪误差导数与R（t）是有界矩阵，L（t），R（t）∈Rm×r。

4 控制算法的收敛性和收敛速度分析

上节提出了改进的迭代控制算法，本节对算法控制律进行理论分析，验证其收敛性和收敛速度。

4.1 收敛性分析

引理1［9］：设实数序列｛αk｝，满足ak≤ηak－1＋bk，0≤η＜1，其中bk也为实数序列，若有b∞，则有

引理2［9］：设u（t），v（t）为区间［0，T］上的非负连续函数，且存在非负常数M，q，使得

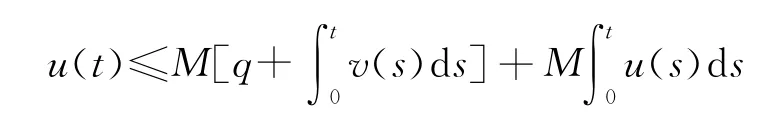
则

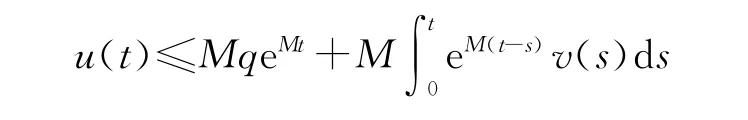
关于引理的说明，在引理中，如果取v（t）≡0，u（t），v（t）为区间［0，T］上的非负连续函数时，在满足条件

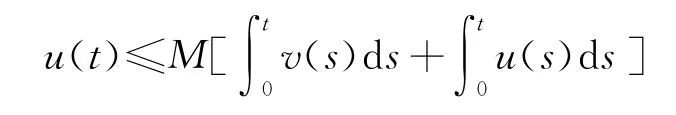
有下式成立

分析如下：设函数g关于x与t的偏导数存在，分别用gx与gt表示，并且B，g，gx，gt有界，其界分别记为bB，bg，bgx，bgt，设

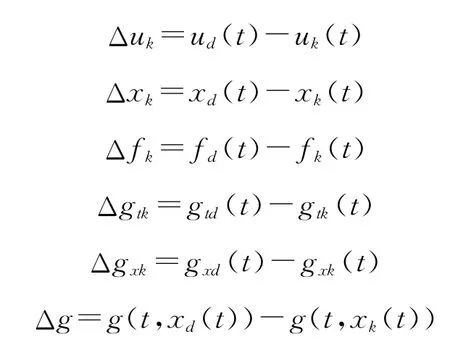
初始控制量u0（t）是一个有界函数。

对于非线性时变系统，满足学习律式（13）条件下，如果有‖α－RgxdBxd‖≤β＜1，则当k→∞时，有跟踪误差一致收敛。

为了方便起见，在不影响证明正确性的同时略去时间变量t。有

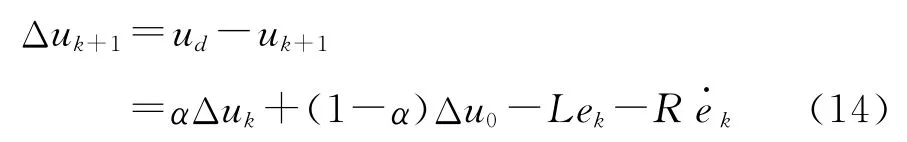
考虑，由式（11）、式（12）、式（13）可得，

在知识与信息飞速增长爆炸的时代，如何鉴别信息的真实性、准确性与有效性已经成为了当下的关键。因而，当今科学教育的研究潮流中批判性思维的培养已经成为了一个重要且亟待研究的方向，深度学习的基本特征中同样包含了这点——对所学知识及其学习过程进行评判。生物学学科的教材内容体系与教师知识水平随着生物科技的发展也需要不断更新，学习过程为中心已经渐渐取代了多年前适用的教授过程为中心。前期的研究表明： 逆向化的教学主线应用在生物学模型课的教学中，能够让学生在评价知识与学习过程的同时，让学生加强对学科知识的理解、学科思维的掌握以及学科精神的培育等[7]。

将式（15）代入式（14），可得

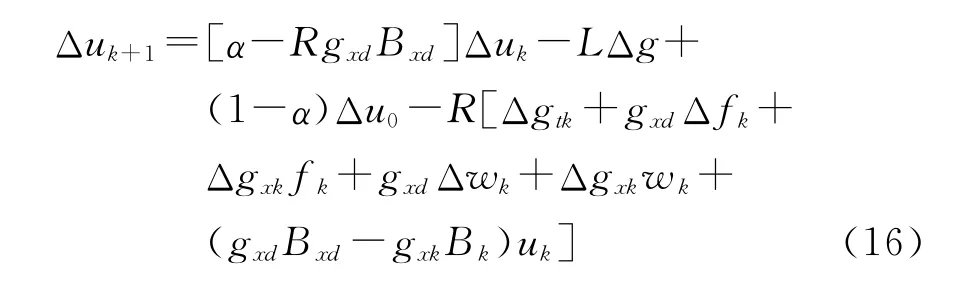
对式（16）两边同取λ范数，利用Lipschitz条件，可得下式

其中

式中，bL，bR分别为学习增益矩阵L（t）与R（t）的界；bgx，bf，bu，bw分别为函数gx，f，u，w的界；kg，kgt，kf，kgx，kw，kgxB分别为相应的 Lipschitz常数。

对‖Δxk‖进行分析可得

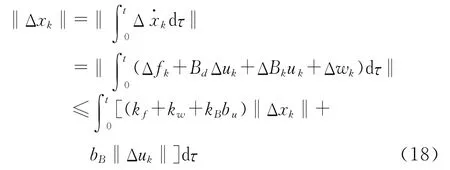
由引理2可得

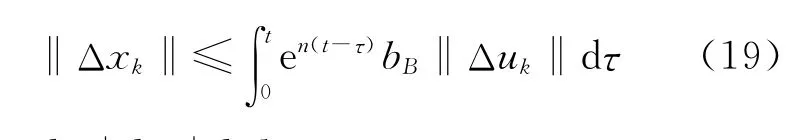
式中：n＝kf＋kw＋kBbu。

继续对式（19）进行变换，有

将式（20）代入到式（17），可得

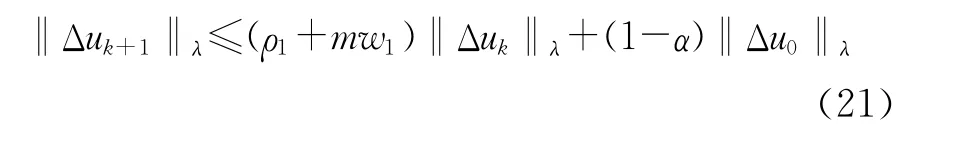
由式（17）可知‖Δuk（t）‖λ一致有界，同理可证一致有界。

4.2 收敛速度分析

定义［10］：设ρ为迭代学习控制算法的收敛条件，将 收 敛 速 度 定 义 为：v＝ρ－（k＋1），k为 迭 代次数。

采用同收敛性分析相同的推导过程可以得出在传统的开环PD型迭代控制中有：

式中：ρ2＝‖1－RgxdBxd‖。

在所提出的控制算法式（21）中，当位置误差不断减小α→1时，可得

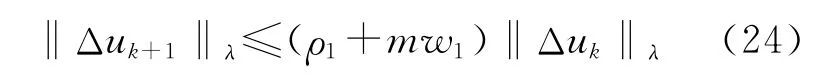
当选用足够大的λ时，可以保证w1→0，从而mw1→0，式（23）、式（24）可以简化为

在直线电机模型中，0≤α≤1，从而有

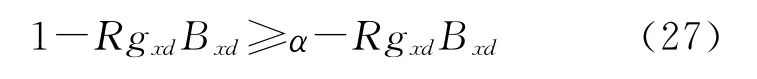
对式（27）两边同时取范数，根据ρ1，ρ2的定义有：

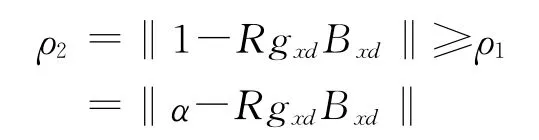
根据收敛速度的定义可得出v2＜v1，即改进型迭代算法的控制量衰减到期望控制量的速度比传统的迭代算法快，从而可以得出改进型迭代算法的收敛速度要优于传统迭代算法。

5 仿真验证及实现分析

为了验证改进型迭代学习控制方法在永磁直线同步电机位置跟踪系统中的控制效果，采用Matlab7.6对本文所提出控制策略进行仿真研究，并与传统开环PD型迭代学习控制方法进行比较。永磁直线同步电机的参数为［11-12］：M＝10 kg，B＝1.2N·s／m，Kf＝25N／A。推力波动Fef＝30sin（25t）N，负载阻力Fl＝100N，摩擦参数分别为：fc＝10，fs＝20，vs＝0.5，fv＝10。L＝150，R＝20。由于在实际的运行过程中直线电机的位置在控制过程中不可能每次都从原点开始，所以有y（0）≠yd（0），选择y（0）＝0.5。参考输入信号yd（t）＝0.5sin（6πt）m。选择迭代次数为10次。图2～图6是经过10次迭代之后的位置跟踪曲线和误差曲线。

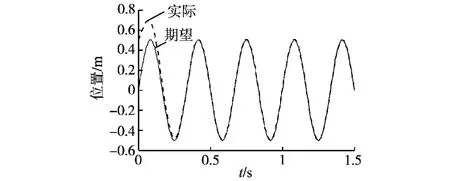
图2 改进型迭代学习控制下PMLSM位置响应曲线Fig.2 Position response curves of PMLSM in improved iterative learning control algorithm

图2、图3分别为改进型迭代学习控制与传统迭代学习控制下位置跟踪响应曲线。对比两图可以看出图2的跟踪速度明显快于图3。图4、图5分别为两种算法下控制量的收敛效果图，比较两图可以看出图4中的控制量收敛到期望控制量所用的时间要比图5少而且振荡的幅值小，即电机开始阶段输出振荡减弱。图4中的控制量在波峰波谷处变化比较频繁是由于摩擦力的存在，只有控制量做出相应的变化才能保证控制精度的提高。图6为两种方法的跟踪误差比较，从对比中可以看出，在3种扰动（推力波动、摩擦力、负载扰动）的影响下，改进型迭代学习控制具有较强的扰动抑制能力，跟踪精度也得到明显改善。

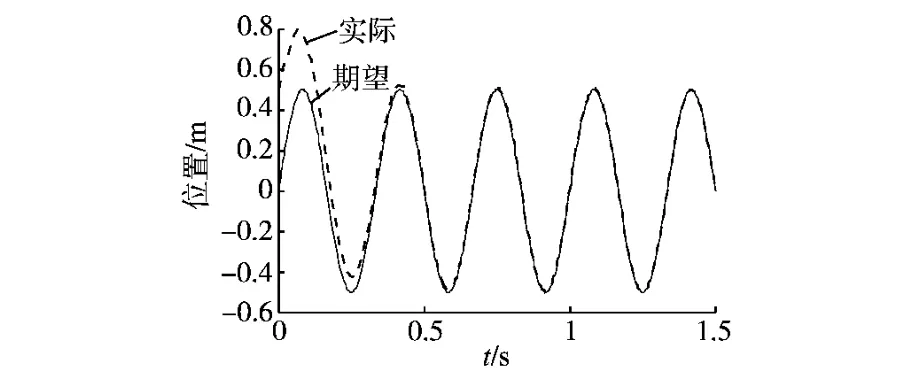
图3 传统开环PD迭代学习控制下PMLSM位置响应曲线Fig.3 Position response curves of PMLSM in traditional open loop PD－type learning control algorithm

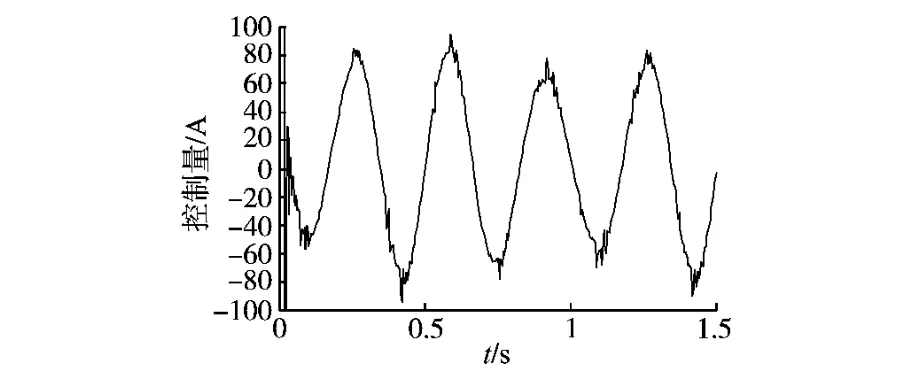
图4 改进型迭代学习控制算法下的控制量Fig.4 Control input in improved iterative learning control algorithm

图5 传统开环PD迭代学习控制算法下的控制量Fig.5 Control input in traditional open loop PD－type learning control algorithm

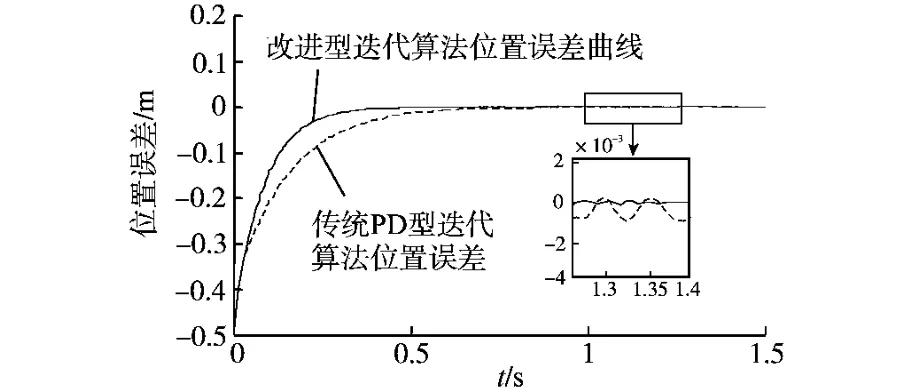
图6 两种方法位置跟踪误差曲线对比Fig.6 Contrast of position tracking error curves of two method

6 结论

本文通过对传统迭代算法进行改进，提高了直线电机伺服系统在工作中的响应速度与跟踪精度。对于直线电机伺服系统在高速高效加工中的快速响应以及高精度的要求，该文所提出的算法具有参考价值。

［1］郭庆鼎，孙宜标，王丽梅.现代永磁电动机交流伺服系统［M］.北京：中国电力出版社，2006.

［2］关丽荣，姜彤.基于自适应变结构永磁直线电机直接推力速度控制［J］.电气传动，2008，38（9）：72－74.

［3］郝双晖，蔡一，郑伟峰，等.基于前馈控制的交流伺服系统高速定位控制［J］.微特电机，2010，38（2）：35－40.

［4］杨俊友，门博，马航，等.基于迭代学习的永磁直线同步电动机扰动抑制［J］.沈阳工业大学学报，2010，32（1）：6－10.

［5］马珍珍，南余荣.基于迭代学习的永磁同步直线电动机的位置环控制［J］.微特电机，2008，36（4）：49－51.

［6］姚中舒，吴键荣，杨成梧.基于神经网络的学习控制及其在机器人中的应用［J］.电工技术学报，2003，18（3）：72－76.

［7］张代林，陈幼平，艾武，等.基于观测器模型的直线电机干扰抑制技术的研究［J］.中国电机工程学报，2007，27（12）：14－18.

［8］孙瑜，李志安，林辉.一类含控制时滞非线性系统在任意初始值下的开环PD型迭代学习控制［J］.兵工学报，2010，31（6）：837－841.

［9］谢胜利，田森平，谢振东.迭代学习控制的理论与应用［M］.北京：科学出版社，2005.

［10］Piao F X，Zhang Q L，Xu J X，etal.Convergence Speed Analysis of Iterative Learning Control Approaches［C］∥IEEE Conference on Industrial Electronics and Applications，2006：1－4.

［11］张霖，党选举，曾思霖.永磁同步直线伺服系统的一种双模控制［J］.电气传动，2010，40（2）：53－56.

［12］Tan K K，Huang S N，Lee T H.Robust Adaptive Numerical Compensation for Friction and Force Ripple in Permanent－Magnet Linear Motors［J］.IEEE Trans.on Magnetics，2002，38（1）：221－228.