基于重复控制的三相4线制有源电力滤波器研究

，

（教育部光伏系统工程研究中心，合肥工业大学能源研究所，安徽 合肥 230009）

1 引言

随着电网中非线性、不对称、冲击性负载的大量增加，带来了严重的谐波、无功功率、三相不平衡等电能质量问题，对电力系统造成了严重的污染。有源电力滤波器是一种用于动态抑制谐波和补偿无功的电力电子装置，可以很好地对上述电力污染进行有效的治理［1］，由于三相3线制有源电力滤波器只有2个自由度，对于存在零序电流的负载类型无法将其补偿为三相对称，而三相4线制有源电力滤波器具备零序电流通道，补偿非线性或不平衡负载时可以将电网中三相电流补偿成对称，避免将不平衡电流引入电网，并且减小了零线中的电流，提高电网的稳定性。通过基于瞬时无功功率理论的ip－iq算法［2］可以对三相4线制负载中的谐波及无功电流进行准确快速的检测，根据三相4线制有源电力滤波器的特点重新设计重复控制器［3］，该方案具有结构简单，稳态精度高的特点，通过实验证明了所提方法的有效性。

2 系统结构及谐波检测

2.1 三相4线制系统结构

三相4线制系统结构如图1所示，这里采用控制方法简单、直流侧电压利用率较高的三相4桥臂拓扑结构［4］，由第4对桥臂产生零线补偿电流icn，使其与负载零线电流iLn大小相等方向相同，从而抵消电网侧的零线电流。其中负载由三相整流桥和单相纯电阻负载构成。有源电力滤波器基本工作过程是检测负载中的三相电流和零线电流，经过指令电流计算电路求得补偿电流的指令信号，再通过控制算法生成PWM信号驱动功率开关器件从而产生所需的补偿电流，最终使经补偿后的电网电流中只含三相平衡基波电流。

图1 三相4线制有源电力滤波器系统结构Fig.1 System architecture of three－phase four－wire APF

2.2 指令电流运算电路

为了使电路锁相更准确，本文采用三相锁相环结构，可以使电路即使在电压波形畸变时也能完成正常锁相，提高了锁相的准确性。指令电流计算方法如图2所示，首先将零序分量从三相电流中剔除，去除零序分量后的三相电流可以利用三相3线制情况下的检测方法［5］进行检测，进而求出三相4线制系统中的谐波、基波负序、零序在内的补偿电流指令信号，同时得到零线补偿电流指令信号。为了使直流侧电压保持恒定，在基波有功电流计算中加入了直流电压调节量，使有源电力滤波器在补偿谐波电流的同时吸收一定的有功电流抵消系统损耗，维持自身的正常工作。

图2 谐波指令电流计算原理图Fig.2 Schematic of harmonic current detection

图2中方框计算公式如下：

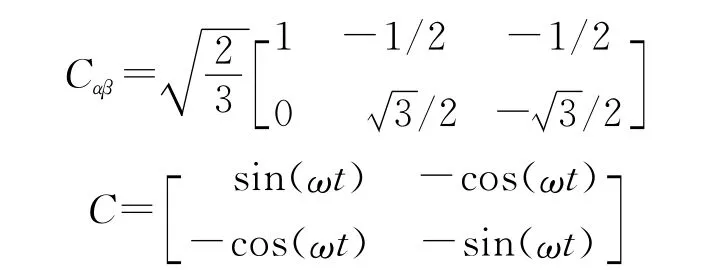
C－1是对应的逆变换。三相电流零序分量为i0＝（ia＋ib＋ic）／3。将三相电流中零序分量剔除可得：

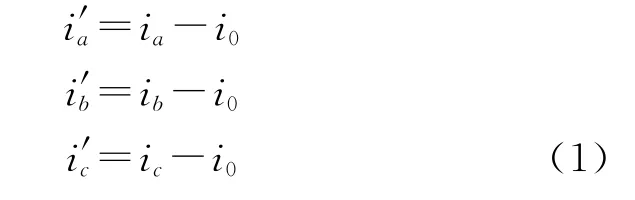
由公式（1）采用文献［1］介绍的基于瞬时无功功率的谐波检测方法，得出其中的基波正序分量如下：

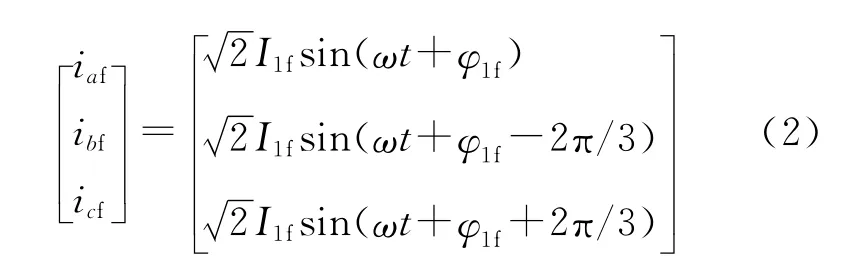
而零序补偿电流

当需要同时补偿谐波及无功分量时，只需断开iq通道，只对ip进行反变换即可。将式（2）与原电流相减后，得出包含谐波、基波负序、零序在内的三相补偿指令电流

3 重复控制器设计

3.1 有源电力滤波器结构模型

图1中的滤波器采用LCL结构，如图3所示，采用4桥臂结构时主电路各相对称，通过对指令电流分析可知，补偿电流和零线电流的产生可以看作是各对桥臂独立完成［5］的，故此处只对A相电路进行分析，其他各相可类似推得。有源电力滤波器单相等效结构如图4所示。图4中L1为逆变器侧滤波电感，L2为电网侧滤波电感，R1，R2分别为电感L1，L2的等效串联电阻，C为滤波电容，Rd为阻尼电阻，ui为逆变器输出电压，us为电网相电压。

图3 LCL型滤波器结构Fig.3 The structure of LCL filter

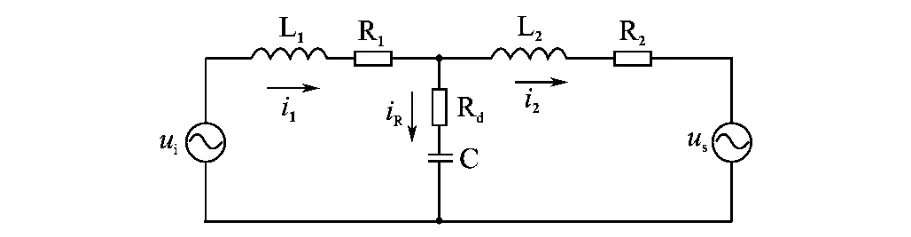
图4 有源电力滤波器单相等效结构Fig.4 Equivaleut circuit of single－phase APF

由图4可列如下方程：

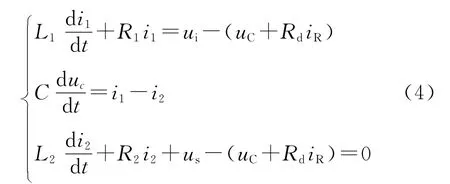
考虑到R1，R2很小，在等效分析时可以忽略，对式（4）化简，并进行拉氏变换可得从逆变器输出电压ui到电网侧输出电流i2传递函数为

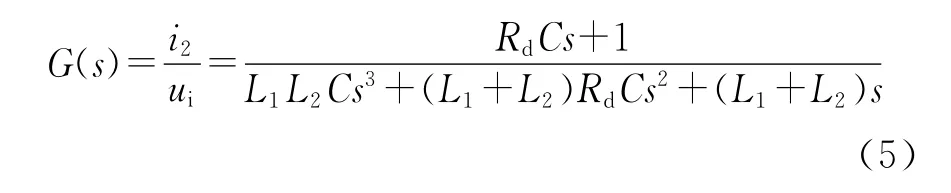
选取有源电力滤波器参数［6］为：L1＝0.5mH，L2＝0.19mH，Rd＝0.005Ω，C＝20μF。

3.2 补偿器S（z）设计

控制系统框图［7-9］如图5所示，图5中Q（z）是滤波器，与z－N一起构成重复控制器内膜，简化设计时可将Q（z）设计为一个小于1的常数，避免“纯积分”在单位圆上的N个开环极点造成的临界振荡状态。S（z）是补偿器，对控制对象G（z）进行补偿校正，使其满足控制性能要求。

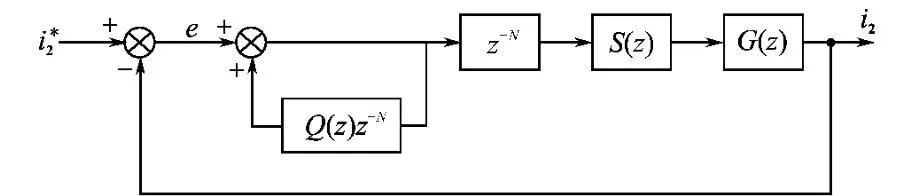
图5 重复控制器结构框图Fig.5 The block diagram of repetitive controller

系统采样频率取12kHz，针对所选滤波器参数进行重复控制器设计，将主电路参数代入式（5）可得控制对象传递函数为

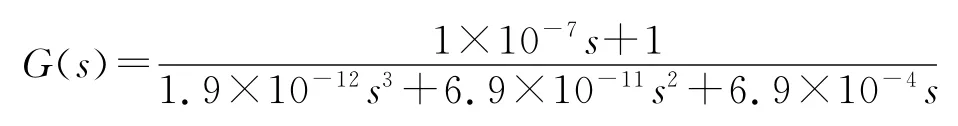
其波特图［10］如图6所示。从图6可知LCL滤波器在高频段具有－60dB十倍频的衰减，但在3kHz频率处有谐振出现，因此需要通过补尝器S（z）校正滤波器提高滤波性能。

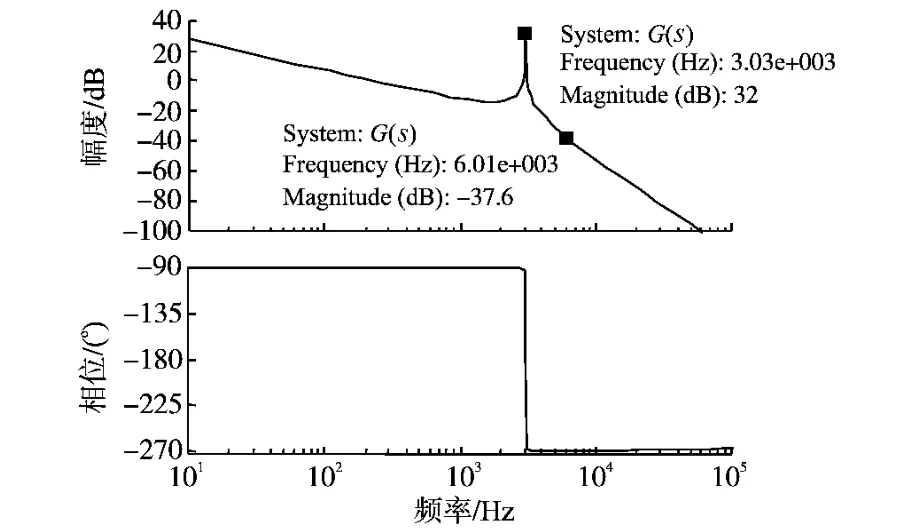
图6 LCL滤波器波特图Fig.6 Bode plot of LCL filter

设补偿器：

式中：Fn（z）为陷波器；F2（z）为二阶滤波器；D（z）为微分补偿环节；zM为超前环节。

3.2.1 陷波器Fn（z）设计

图7 陷波器Fn（z）波特图Fig.7 Bode plot of trap filter Fn（z）

3.2.2 二阶滤波器F2（z）的设计

由图6可见LCL滤波器谐振频率3.033 kHz，设计的系统带宽为2.5kHz（补偿50次谐波），因此取二阶滤波器的截止频率ω为2.6 kHz，阻尼比ξ为0.707，其传递函数为

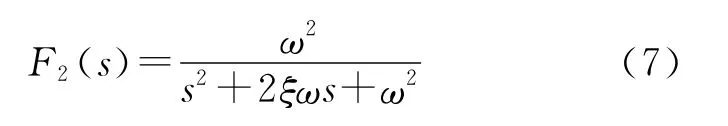
采用双线性变换离散化有：

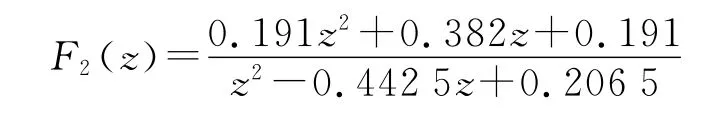
3.2.3 补偿器D（z）设计

D（z）环节用以抵消LCL滤波器在低频段对信号增益造成的衰减，由于滤波器在低频段的特性与单电感（L1＋L2）时相近，故可将其设计成准微分环节，再离散化为z域形式。有D（s）＝其中k等于总电感（L1＋L2），将惯性环节转折频率定为1kHz，可得其离散域传递函数：

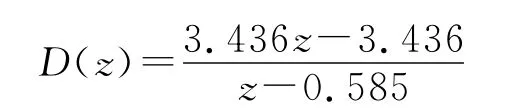
3.2.4 超前环节确定

通过对系统波特图分析以及对逆变器固有延时的考虑，确定超前3拍，即取M＝3。

综上可知设计补偿器为

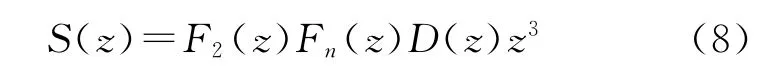
经补偿后的系统开环传递函数为

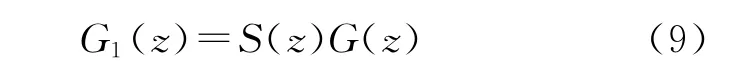
其波特图如图8所示，可见系统在低频段具有零增益零相移特性，而在高频段尽管有较大相移，但随着其频率的增加，幅值呈快速衰减，故满足控制系统的要求。

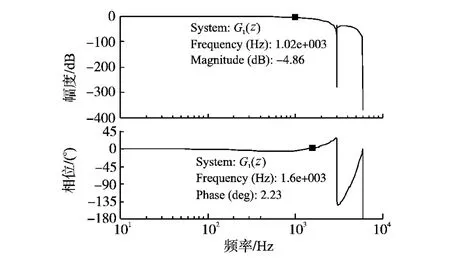
图8 经S（z）补偿后控制对象G（z）的波特图Fig.8 Bode plot of G（z）compensated by S（z）

3.3 重复控制器设计

根据重复控制器框图5可知重复内膜：

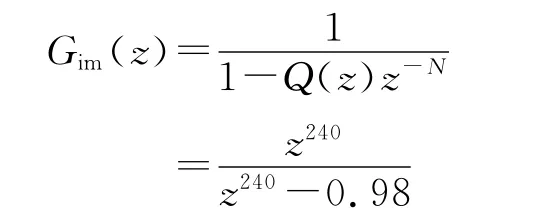
其中，N为每基波周期采样点数取240，Q（z）＝0.98，z－N是周期延迟环节，为通过超前环节进行控制对象的相位校正提供条件。重复内膜的频率特性如图9所示，可见重复内膜能为基波和各次谐波提供34dB增益，且几乎不会造成相位偏移。

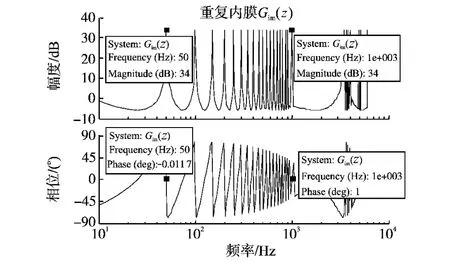
图9 重复内膜Gim（z）波特图Fig.9 Bode of Repeat internal－model Gim（z）

重复控制系统稳定性［7］分析，根据小增益原理［3］重复控制的稳定性条件为

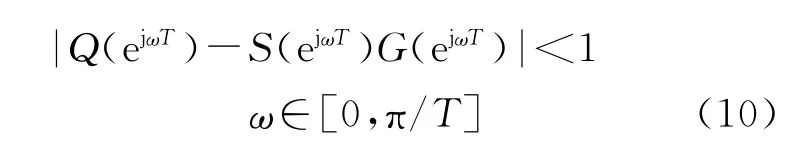
式中，T为采样周期，其几何描述如图10所示，系统稳定条件是频率ω从0变化到π／T时矢量S（ejωT）G（ejωT）的末端划过的轨迹不超出以（Q（ejωT），0）为圆心的单位圆。由图10可见加入重复控制后系统依然稳定。

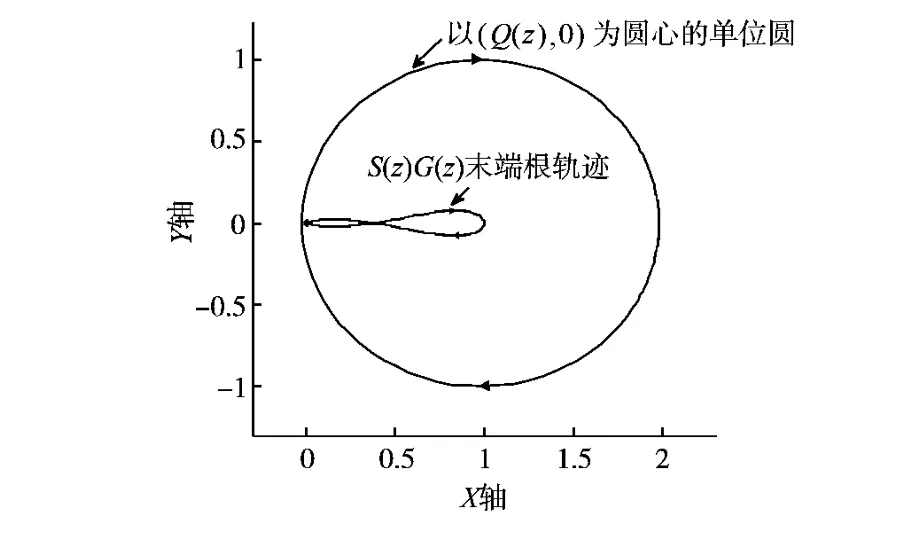
图10 S（z）G（z）末端根轨迹Fig.10 End root locus of S（z）G（z）

4 实验结果与分析

对本文所提出的控制方法设计实验样机进行实验验证，测得三相电网电压为230V／50Hz，用三相整流桥和单相纯电阻构成三相4线制不平衡非线性负载，其中负载R1＝55Ω，R2＝55Ω；直流母线电压730V；开关频率6kHz。主控芯片采用Freescale公司的56F8356 16位DSP，其主频为60MHz，采样频率12kHz。使用泰克TDS3054C示波器和FLUCKE434电能质量分析仪对实验结果进行记录分析。

图11～图13分别为三相4线中不平衡负载电流、并联型有源电力滤波器输出补偿电流、补偿后电网电流，图11～图13中由上至下分别为A，B，C相电流；图14所示由上至下依次为负载和电网中零线电流；图15a、图15b依次为补偿前后A相电网电流的谐波分析图。

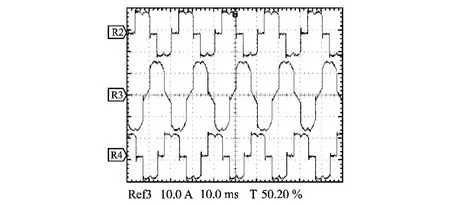
图11 负载电流波形Fig.11 Load current waveform

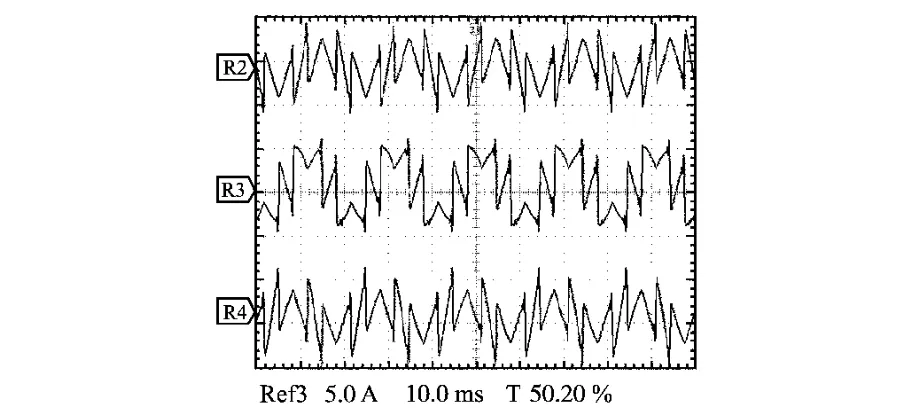
图12 有源电力滤波器输出补偿电流Fig.12 Output compensating current of APF

图13 补偿后电网电流Fig.13 Grid current waveform after compensateing

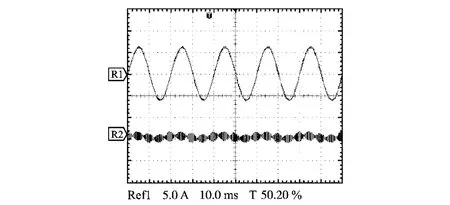
图14 零线电流Fig.14 Neutral line current

图15 A相电网电流补偿前后谐波分析Fig.15 Harmonic analysis of Aphase grid current before and after compensating

从图11中可以看出负载三相电流不对称，电流波形严重畸变。由图12可以看出由于有源电力滤波器系统需要补偿不平衡三相4线制负载，故其所输出补偿电流亦为三相不对称。由图13可见在经过有源电力滤波器补偿后三相电网电流基本对称，且只含基波电流。从图14可以看出负载零线中的大部分电流都由有源电力滤波器提供，电网零线电流只有很小的余量。图15a、图15b分别为A相电网电流补偿前后谐波分析图。可以看出经过有源电力滤波器补偿后电流中谐波含量由原来的29.5%降为4.5%，达到了电网的规范要求。

5 结论

本文介绍了三相4桥臂有源电力滤波器工作原理和控制系统设计方法。首先利用将零线电流分离的ip－iq法对三相4线制系统谐波进行实时检测，然后设计出适用于有源电力滤波器系统的重复控制器，文中给出了有源电力滤波器系统的组成结构及控制策略设计过程；在判定系统稳定的基础上，设计实验样机进行谐波补偿，实验结果表明了该方案的正确性，通过利用有源电力滤波器进行谐波和无功补偿后电网中的电能质量得到了很大的提高。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，2010.

［2］卓放，杨君，胡军飞，等.三相四线制系统并联型有源电力滤波器实验研究［J］.电力电子技术，1999（6）：16－18.

［3］仇志凌.基于LCL滤波器的三相三线并网变流器若干关键技术研究［D］.杭州：浙江大学，2009.

［4］乐健，姜齐荣，韩英铎.基于统一数学模型的三相四线并联有源电力滤波器的性能分析［J］.中国电机工程学报，2007，27（7）：108－114.

［5］卓放，杨君，胡军飞，等.三相四线制有源电力滤波器主电路的结构形式与控制［J］.电工电能新技术，2000（2）：1－6.

［6］刘飞，查晓明，段善旭.三相并网逆变器LCL滤波器的参数设计与研究［J］.电工技术学报，2010，25（3）：110－116.

［7］仇志凌，杨恩星，孔洁，等.基于LCL滤波器的并联有源电力滤波器电流闭环控制方法［J］.中国电机工程学报，2009，29（18）：15－20.

［8］王斯然，吕征宇.LCL型并网逆变器中重复控制方法研究［J］.中国电机工程学报，2010，30（27）：69－75.

［9］武健，何娜，徐殿国.重复控制在有源电力滤波器中的应用［J］.中国电机工程学报，2008，28（18）：66－72.

［10］赵广元.MATLAB与控制系统仿真实践［M］.北京：北京航空航天大学出版社，2011.