交流伺服系统参数辨识策略研究

，，，

（1.华中科技大学 控制科学与工程系，湖北 武汉 430074；2.中国地质大学 机械与电子信息学院，湖北 武汉 430074）

在电机驱动应用领域里，要求系统对负载变化和速度改变有很好的动态响应，以及对电机参数变化有良好的鲁棒性。然而永磁同步电机（PMSM）转动惯量和负载转矩的变化会严重影响系统的性能，为达到伺服系统高精度控制的良好动态和静态特性，需要在线辨识系统的负载转矩和转动惯量，同时相应地调节控制器的参数。

转动惯量辨识采取的方法主要分为离线辨识和在线估算两大类。离线辨识是通过点击转速给定端施加特定的速度给定信号，测得电机实际速度的稳态和动态响应，再通过周期积分［1］或者线性最小二乘法［2］等辨识出电机的转动惯量。转动惯量的在线估算则是通过分析电机对外部的扰动信号响应通过观测器法得到信号，再采取诸如卡尔曼滤波器［3］，最小方差扩展递归算法［4］得到转动惯量的估计值。本文采用离线方法辨识伺服系统的转动惯量和负载转矩。

1 PMSM的数学模型

假设永磁材料的电导率为零，转子上没有阻尼绕组，相绕组中感应电动势波形为正弦，并且忽略铁芯饱和，不计涡流和磁滞损耗，则面装式PMSM在d－q坐标系下电压方程为

电磁转矩方程为

电机运动方程为

式中：ud，uq分别为d，q轴定子电压；id，iq分别为d，q轴定子电流；Ld，Lq分别为d，q轴定子电感；p为微分算子；Ψf为永磁体基波励磁磁场交链过定子绕组的磁链；ωr为转子电角速度；B为粘滞摩擦系数；Te为电磁转矩；Tl为负载转矩；J为转子和所带负载的总转动惯量；ωm为电机机械角速度［5］。

2 转动惯量、负载转矩辨识算法

在电机运动方程式（3）中，可以通过测量得到的参数有电磁转矩信号Te以及电机的机械角速度信号ωm，需要通过已知信号进行参数估算和辨识的量是负载转矩Tl、总转动惯量J和风载摩擦系数B，因为辨识的主要目的是得到负载转动惯量，所以将与转动惯量辨识值无关的量合并为一项。

其中，为总转动惯量的辨识值，它与实际转动惯量存在误差，记为ΔJ；为扰动转矩的辨识值，其表达式为

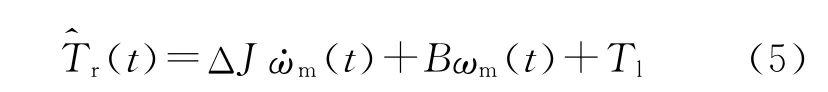
由式（5）可以看出，转动惯量只有在速度发生变化时才能对输出转矩有影响，而扰动转矩中又包含和转动惯量无关的项Bωm（t）和Tl，因此需要选特定的速度给定信号，并利用数学方法消除无关项。

要消除转动惯量辨识无关项，首先要做出如下假设。

与PMSM伺服系统电流环时间常数相比，负载转矩变化缓慢，在中断处理中可视为常量，由于电流环响应迅速，而电机转速变化属于速度环的响应，时间常数相对电流环来说比较大，因此这个假设在实际工况中成立。

选取一个周期为T的测试速度信号即ωm（t）＝ωm（t＋T），将测试速度信号的微分量（t）乘到式（5）的两端，并在一个周期内进行积分，结果如下：

对式（6）左边第2项即风载摩擦引起的扰动转矩积分项进行如下处理：

可以得到，该扰动转矩在一个周期下的积分作用为零。同样道理，对式（6）左边的第3项，即负载扰动转矩作同样处理，则可以得到负载转矩在一个周期的积分累积作用也为零。消除与转动惯量辨识的无关项，式（6）可简化为

则式（8）表明，通过选取恰当的周期速度给定信号，可以消除与转动惯量辨识无关的变量，对式（8）做进一步整理和变化，可以得到总转动惯量辨识的理论递推式：

综合上述，只要选取合适的速度周期信号，就可以比较准确地辨识出伺服系统的总转动惯量和负载转矩，考虑实际应用场合对电机和机械结构的保护，本文选择加减速比较平滑、幅值较小的正弦信号作为周期速度参考信号。

3 转动惯量、负载转矩辨识方案

永磁同步电机采用转子磁场定向的双环控制策略，实现定子电流的励磁分量和转矩分量的线性解耦，PMSM双环控制结构框图如图1所示。

图1 PMSM双环控制结构框图Fig.1 Double－loop control block diagram of PMSM

根据上面提到的辨识算法，搭建负载扰动转矩的辨识结构框图和总转动惯量的辨识结构框图如图2、图3所示。

图2 负载扰动转矩辨识结构框图Fig.2 The block diagram of load torque identification

图3 总转动惯量辨识结构框图Fig.3 The block diagram of the total inertia identification

4 仿真结果与分析

采用Synopsys公司开发的专业仿真软件Saber作为仿真平台，搭建PMSM双环控制系统仿真模型，同时搭建转动惯量和负载转矩的辨识模块，其Saber仿真结构图如图4所示。

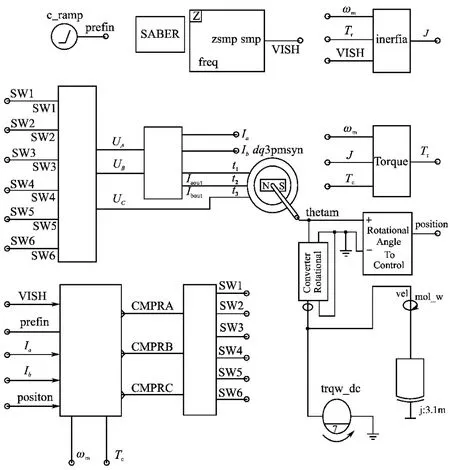
图4 转动惯量辨识和负载转矩辨识仿真模型Fig.4 The simulation model of inertia identification and load torque identification

为保证电流环对电网电压波动的及时抗干扰能力和速度环有良好的抗负载扰动能力，按照工程设计方法，将电流环和速度环都校正成典型Ⅱ型系统，电流环和速度环都采用数字PI控制器。为确保系统的控制精度和防止采样频率过高引起累积误差，电流环的采样周期为0.1ms，速度环的采样周期为0.5ms，逆变器开关频率为10 kHz，永磁同步电机主要参数如下。

额定功率1.57kW，额定转速2 000r／min，定子电阻0.6Ω，定子电感3.1mH，额定电流6A，转动惯量0.96×10－3kg·m2，极对数2，机械时间常数0.66ms，电磁时间常数5.2ms。

系统主要由功率驱动模块、控制算法模块、电机模型、负载、独立的负载转动惯量模块、负载转矩辨识模块和总转动惯量辨识模块组成。其中，功率驱动模块实现220V交流电压不控整流成310V的直流电压，再利用SVPWM驱动信号输出逆变电压，给PMSM供电。控制算法模块主要用代码实现Clarke变换、Park变换和其逆变换、SVPWM、电流调节器和速度调节器等功能。

仿真参数为：给定正弦速度激励信号的幅值100r／min，周期0.2s，仿真时间2s，电机负载转矩7N·m，负载的转动惯量3×10－3kg·m2，则电机的总转动惯量为3.96×10－3kg·m2。下面为给定正弦速度下的仿真结果及说明。

辨识的好坏很大的因素取决于速度的跟随，图5给出了速度给定信号和速度反馈信号的波形，从图5中可以看出两个波形几乎重合，跟随性能良好。

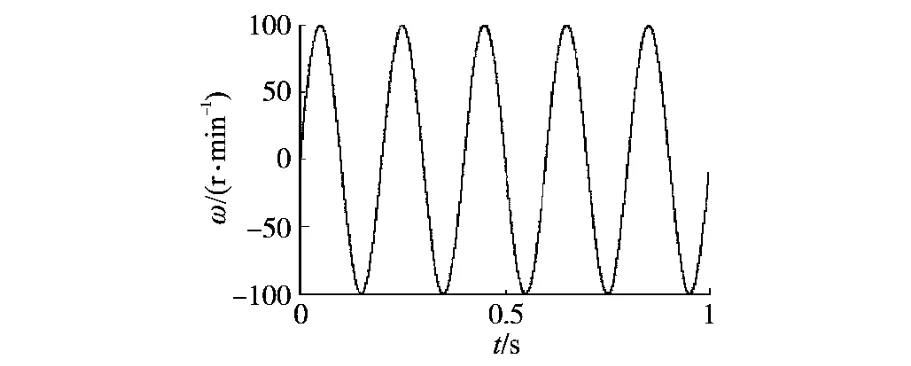
图5 速度给定与反馈的波形Fig.5 The given and feedback velocity′s waveforms

负载转矩的辨识结果如图6所示，在第1个辨识周期0.2s之前，负载扰动转矩辨识波形有很大的波动，这是因为第1个辨识周期转动惯量的初值为0，也就是电机的电磁转矩被认为全部用来克服负载转矩。而在1个周期之后，已经有转动惯量的辨识值输入到转矩辨识模块，但是与实际转动惯量还是有误差，反映到转矩辨识上就表现为正弦的转矩辨识结果。辨识结果在第1个周期之后就已经基本趋于7N·m，辨识误差小于1%，辨识结果有效。

图6 负载转矩辨识结果（Tr＝6.943 5N·m）Fig.6 The result of load torque identification（Tr＝6.943 5N·m）

图7为总转动惯量辨识结果的仿真波形，在第2个周期的辨识结果3.93×10－3kg·m2就已经非常接近实际值，辨识误差小于1%，辨识结果与实际值相吻合。在第2个周期以后的辨识值与实际值十分接近，所以辨识值基本成一条直线。产生稳态误差的原因有很多，其中主要的原因在于速度跟随当中一些细微的误差，从而导致电机角速度反馈波形不是理想的正弦周期信号。

图7 总转动惯量辨识结果（J＝3.93×10－3 kg·m2）Fig.7 The result of the total inertia identification（J＝3.93×10－3 kg·m2）

仿真参数为：仿真时间2s，负载转矩7.5N·m，负载转动惯量8.0×10－3kg·m2，则总转动惯量8.96×10－3kg·m2。

从图8可以看出，在第1个周期J＝0时，输出转矩被认为全部用来克服负载转矩，在第2个周期总转动惯量辨识值为J＾＝8.85×10－3kg·m2，但是仍然要小于实际值J＝8.96×10－3kg·m2，因此，第2周期负载转矩辨识值的波动还是要大于以后的周期。稳定之后，辨识误差在0.5%以内，辨识结果有效。

图8 负载转矩辨识结果（Tr＝7.477 8N·m）Fig.8 The result of load torque identification（Tr＝7.477 8N·m）

从图9看出，第2个辨识周期辨识出来的总转动惯量J＝8.85×10－3kg·m2与实际值存在一定的误差，其主要原因是因为第1个周期的电机转速相对来说没有很好地跟随给定。稳定之后的辨识误差在0.5%以内，辨识结果有效。

图9 总转动惯量辨识结果（J＝8.85×10－3 kg·m2）Fig.9 The result of the total inertia identification（J＝8.85×10－3 kg·m2）

5 结论

本文提出了交流永磁同步伺服系统机械参数辨识算法，基于电机运动方程的转动惯量和负载转矩的辨识算法具有实时性好、收敛速度快等优点，此外，该算法可以辨识的负载范围宽，对物理实现有很好的理论指导意义，并且通过Saber仿真结果验证了这种方法的可行性和有效性。

［1］Shinichi Kobayashi，Ichiro Awaya，Hiroshi Kuromaru，etal.Dynamic Model Based Auto－turning Digital Servo Driver［J］.IEEE Transactions on Industrial Electronics，1995，42（5）：462－465.

［2］Lin W M，Su T J，Wu R C，etal.Parameter Estimation of Induction Machines under No－load Test［C］∥IEEE Conference on Industrial Electronics and Applications，2010，5th：1762－1767.

［3］Choi J－W，Lee S－C，Kim H－G.Inertia Identification Algorithm for High－performance Speed Control of Electric Motors［J］.IEE Proc.－Electr.Power Appl.，2006，153（3）：379－386.

［4］Hong Seok－Joon，Kim Heui－Wook，Sul Seung－Ki.A Novel Inertia Identification Method for Speed Control of Electric Machine［J］.IEEE Transactions on Industrial Electronics，1996，25（8）：1234－1239.

［5］沈艳霞，刘永钦.基于改进型模型参考自适应的PMSM参数辨识［J］.电气传动，2009，39（5）：47－50.