异步电机速度自适应磁链观测器的研究

（1.中国科学院 电工研究所，北京100190；2.中国科学院 研究生院，北京 100049）

1 引言

在无速度传感器电机控制过去的研究中，大部分的研究集中在电机低速运行时如何取得稳定精确的转矩或速度控制，而高速下电机运行很少有文献涉及［1 7］。然而应用于电动汽车的异步电机在高速情况下的稳定运行对磁链观测器提出了更高的要求，也就意味着磁链观测器应具有快速的响应跟踪能力。通常将磁链观测器的特征值配置在被观测电机特征值相同的位置［6］，此时的磁链观测器综合了电流磁链模型和电压磁链模型的特点，对主要电机参数具有较好的鲁棒性，但是随着电机运行速度的提高，采用这种配置方式的磁链观测器不能及时跟踪实际磁链与转子速度信号的变化；另外，将磁链观测器的特征值配置为被观测电机特征值k倍位置（k＞1），以提高观测器的响应速度［1 2］，这种配置方式也不能满足电机高速运行的需要；将速度自适应磁链观测器配置为电压磁链模型，尽管能在高速下获得较好特性，但也存在着纯积分环节的物理实现或是低通滤波器截止频率的选择问题［8］。本文提出了一种新的观测器极点配置的方法，这种方法能够使得观测器在高速情况下保持收敛稳定的特性，并在此基础上通过增加弱磁调速时的速度估计环节中的比例积分值，克服了高速下磁通降低带来的速度估计环增益降低的问题，保证了速度观测器的精确性，最后通过仿真与试验对所提出算法进行了验证。

2 异步电机数学模型

选择定子电流和转子磁链为状态变量，异步电机在两相同步旋转坐标系下的状态方程为

其中

式中：is为定子电流；Ψr为转子磁链；Us为定子电压矢量；Rs，Rr分别为定子电阻和转子电阻；Ls，Lr，Lm分别为定子电感、转子电感和励磁电感；σ为漏感系数；ωe，ωr，ωs分别为同步角速度、转子角速度和滑差角速度。

相应的由电机状态方程可知观测器的状态方程为

其中

式中：上标“＾”表示观测值；G为观测器的反馈增益矩阵。

观测器结构框图如图1所示。

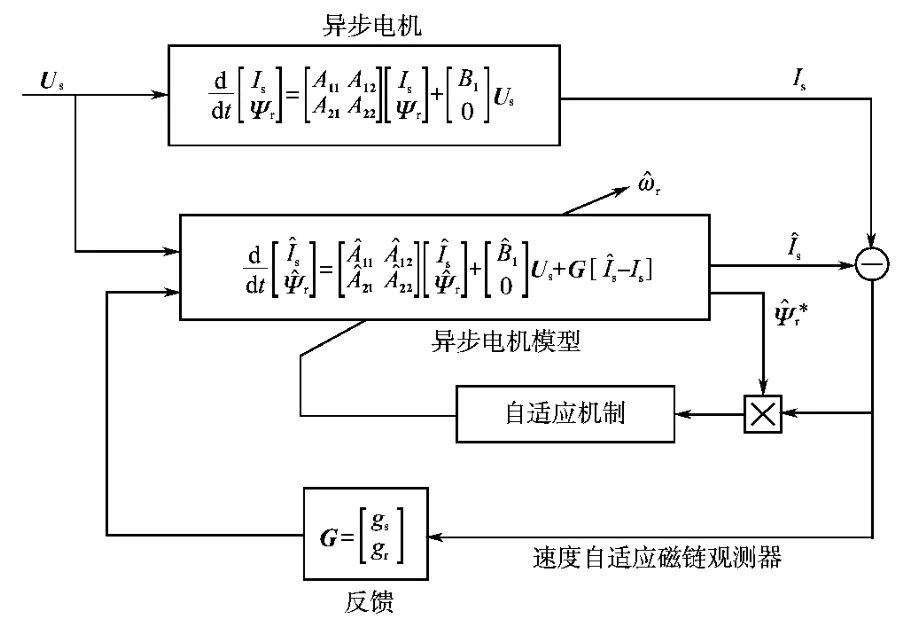
图1 速度自适应磁链观测器方框图Fig.1 Diagram of speed adaptive flux observer

由Lyapunov稳定理论可知速度自适应机

制为

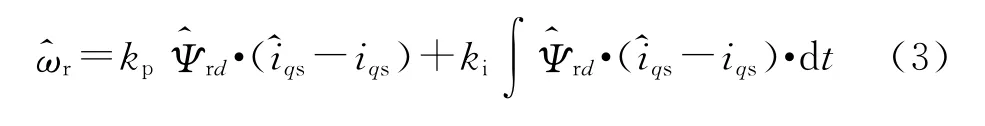
3 速度估计器的改进

异步电机在高速运行时需要采用弱磁调速策略。然而，观察自适应速度机制式（3）中，当减小时，同样大小的定子电流误差产生的积分误差信号更小，所以，弱磁调速会减小速度估计器的增益，从而降低速度估计的带宽。为了在高速下维持速度估计环的跟踪能力，需要对弱磁调速的影响进行相应的补偿。采用的方法是在弱磁调速时相应地增加速度估计器中的PI参数，如下式所示：

式中：k′i，k′p分别为电机基速下运行时的积分和比例；ωbase为电机基速。

4 观测器特征值的配置

4.1 传统的磁链观测器特征值配置方法

到目前为止，异步电机无速度传感器的速度自适应磁链观测器特征值配置方式主要采用零反馈环设计。通常在低速的情况下，电流磁链模型的鲁棒性要好于电压磁链模型，而电压磁链模型在高速时的表现更好，所以更倾向于通过合适的反馈设计将自适应观测器构建成电流和电压磁链模型的组合，所以零反馈环设计能够取得最合适的控制精确性与对电机参数的鲁棒性。零反馈环设计意味着观测器的特征值被配置为与异步电机本身固有特征值完全一致。需要强调的是，零反馈环设计并不是开环设计，因为定子电流误差仍通过转子速度估计环反馈回磁链观测器，所以它依然是一个闭环系统。

对于任意的一个线性系统，当且仅当这个系统是完全可观时（completely observable），针对这个系统构建的观测器可以具有任意的动态性能。实际应用时，观测器的特征值会被选定为具有负的实部，以便使观测器能够收敛于被观测系统的状态变量；并且在大多数情况下，观测器特征值的负实部的绝对值比被观测系统特征值的负实部绝对值要大，以便观测器能够比被观测系统更快的收敛。理论上讲，特征值可以具有任意的负实部，甚至负无穷大，从而产生非常快速的收敛速度。但是，这种具有过大负实部特征值的办法会使得观测器类似于一个微分器，极大地放大信号中存在的噪声会导致不稳定的情况出现。关于如何选择观测器特征值统一的方法，到目前为止并没有完全的解决；在实际工程中，特征值会被配置成比被观测系统特征值绝对值稍大的负实部，这样会有一个比较好的观测和控制效果。

由现代控制理论可知，观测器稳定性取决于其相应的系统矩阵特征值所在的位置。当所有的特征值处在复平面的左半平面时，系统是收敛稳定的。当系统需要满足特定的暂态性能时，比如说快速性，对噪声的不敏感性等，这就对系统特征值提出了更多的要求。不合理的特征值配置，如特征值虚部过大，特征值实部距离虚轴过远或过近都会引起观测器的振荡，或者响应过慢。

由文献［9］可知，观测器离散后被观测状态的整体误差上限值表达式为

式中：f0为被观测器状态变量的变化频率，50 Hz；f为离散采用频率；F为状态变量的幅值；

由式（7）可知，观测器的观测误差随着被观测状态变量的变化频率f0增加会显著变大，当误差累积到一定水平就会出现不稳定的情况。传统的零反馈设计的特征值分布如图2所示，采用零反馈设计观测器在高速下产生振荡的可能原因有2个：1）定子特征值的虚部过大，当采用Euler法对控制器进行离散化时，过大的虚部将带来振荡；2）转子特征值距离虚轴过近，以至于在高速运行时，观测器不能快速地收敛跟踪异步电机。

解决该问题的办法有2种途径：1）随着被观测状态变量变化频率的提高，提高信号采样以及算法计算速率f；2）增加观测器特征值的大小可以相应降低被观测状态变量的最大误差，本文采用第2种方法。

图2 传统配置观测器的特征值Fig.2 Eigenvalues of observer with traditional configuration

4.2 改进的磁链观测器特征值配置方法

为了获得稳定的控制系统，需要在高速时对观测器特征值进行重新配置，期望的特征值如下式所示：

式中：ωmax为防止负实部绝对值过大而造成信号中的噪声被放大所施加的限制；k1为决定特征值虚部与实部之间的比例关系。

观测器反馈采用下式的配置方式：

其中c是一个正实数，它决定了转子特征值距离虚轴的远近，以此来加快观测器的跟踪速度。

校正后的特征值分布如图3所示（k1＝1，c＝100）。

图3 改进配置观测器的特征值Fig.3 Eigenvalues of observer with improved configuration

在图3中，c＝100，这使得校正后转子特征值与原来转子特征值相比较距离虚轴更远，所以观测器可以很好地跟踪异步电机的状态变量。

5 仿真与实验

通过仿真与试验对速度自适应磁链观测器在高速运行下的情况进行了研究，20kW的三对极异步电机作为被测电机，其具体参数为：定子电阻0.125Ω，转子电阻0.11Ω，励磁电感6.2mH，定子漏电感0.38mH，转子漏电感0.32mH，额定转速2 394r／min，额定电流67A，额定转矩80N·m。

5.1 Matlab／Simulink仿真

采用Matlab／Simulink进行仿真分析。被测电机以额定转矩80N·m从零转速启动，当电机转速达到额定转速2 394r／min（750rad／s）时，电机进入恒功率弱磁运行模式，输出转矩开始下降，当电机转速进一步提高时，电机进入降功运行模式，输出转矩继续下降，如图4所示。

图4 异步电机转矩速度曲线Fig.4 Torque－speed curves of induction motor

当磁链观测器采用传统的零反馈设计时，仿真结果如图5所示。图5中的实线与虚线分别代表实际与观测的励磁电流，转矩电流和转子速度。当转子速度达到4 500r／min（1 400rad／s）时，磁链观测器发生振荡，无法继续跟踪转子磁链信号。

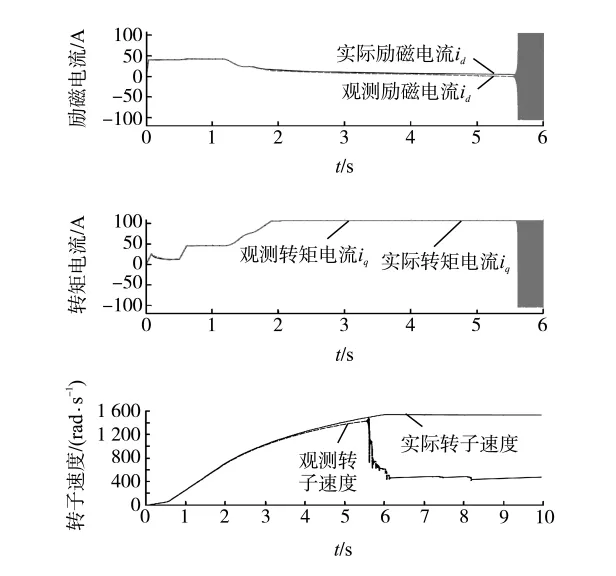
图5 零反馈配置的磁链观测器在高速下的振荡Fig.5 Oscillation of flux observer under high speed operation when G＝0

当磁链观测器采用式（7）反馈配置方法时，仿真结果如图6所示，磁链观测器在转速达到4 800 r／min（1 520rad／s）时依然能够稳定运行。

图6 改进配置方法的磁链观测器在高速下的运行Fig.6 Performance of flux observer under high speed operation with improved configuration method

另外，采用改进前与改进后的自适应机制中比例积分设计方法的仿真如图7所示。图7中实线与虚线分别代表采用传统配置方式时转子速度观测误差与采用改进配置方式后转子速度观测误差，可以发现改进后的速度估计误差明显小于改进前的速度估计误差。

图7 采用传统与改进转速估计方法的速度估计对比Fig.7 Comparison of conventional and improved estimation of rotor speed

5.2 试验结果

采用Infineon的Tricore芯片进行算法实现。选择转子磁链定向矢量控制方式，电流控制器采用典型的同步选择坐标系下的PI控制器［10］，如图8所示。PWM 调制频率为10kHz，采用定子电压重构的方式进行控制［11］。

图8 异步电机无速度传感器矢量控制图Fig.8 Diagram of sensorless controlling of induction motor

在电机试验中，无速度传感器控制器控制被测电机运行在转矩控制模式，驱动电机通过位置传感器运行在速度控制模式。试验结果如图9和图10所示。无速度传感器控制器控制被测电机输出恒定转矩5N·m，并通过驱动电机控制转速从零转速加速至4 800r／min。

图9 高速下异步电机的输出转矩与速度曲线Fig.9 Output torque and speed curves of induction motor under high speed operation

图10 控制器调制电压，采样电流，实际与估计转速信号Fig.10 Signals of modulation voltage，sampling current，real and estimation rotor speed

从图9可以发现，被测电机实际输出转矩有一定的误差，尤其是电机在加速过程中，但是，采用本文提出的观测器配置方法的被测电机在高速运行时能够稳定地运行。图10是被测电机在4 800r／min运行时的无速度传感器控制器采样后的信号，其中图10a是PWM调制器的输入电压信号，图10b是实际的定子电流信号，图10c是估计的与实际的转子速度信号的对比。

6 结论

为了满足电机在高速运行下的需要，本文针对速度自适应磁链观测器对传统速度估计环PI参数设计进行了改进，同时提出了一种适合于高速弱磁情况下的速度自适应磁链观测器反馈设计方法，该方法可以保证观测器在弱磁工作区的稳定运行。因此，速度自适应磁链观测器的反馈环设计方案采用在基速以下，以零反馈环设计结合基速以上，以本文所提出的反馈环设计相结合的办法，可以保证磁链观测器在低速和高速的情况下均取得精确的观测精度。

［1］Kubota K，Matsuse T，Nakmo.DSP－based Speed Adaptive Flux Observer of Induction Motor［J］.IEEE Trans.Ind.Appl.，1993，29（2）：344－348.

［2］Kubota H，Sato I，Tamura Y，etal.Regenerating－mode Lowspeed Operation of Sensorless Induction Motor Drive with Adaptive Observer［J］.IEEE Trans.Ind.Applicat.，2002，38（2）：1081－1086.

［3］Suwankawin S.Sangwongwanich S.Design Strategy of an Adaptive Full－order Observer for Speed－sensorless Induction－motor Drives－tracking Performance and Stabilization［J］.IEEE Trans.Ind.Electron.，2005，53（1）：96－119.

［4］Hinkkanen M.Stabilization of Regenerating－mode Operation in Sensorless Induction Motor Drives by Full－order Flux Observer Design［J］.IEEE Trans.Ind.Electron.，2004，51（6）：1318－1328.

［5］Yang G，Chin T－H.Adaptive－speed Identification Scheme for a Vector－controlled Speed Sensorless Inverter－induction Motor Drive［J］.IEEE Trans.Ind.Applicat.，1993，29（July／Aug）：820－825.

［6］Hinkkanen M.Analysis and Design of Full－order Flux Observers for Sensorless Induction Motors［J］.IEEE Trans.Ind.Electron.，2004，51（Oct.）：1033－1040.

［7］Levi E.A Speed Estimation for High Performance Sensorless Control of Induction Motors in the Field Weakening Region［J］.IEEE Trans.Power Electron.，2002，17（3）：365－378.

［8］Hu J.New Integration Algorithms for Estimating Motor Flux over a Wide Speed Rang［J］.IEEE Trans.Power Electron.，1998，13（5）：969－977.

［9］胡斯登，赵争鸣，袁立强，等.高性能变频调速系统的离散控制问题研究［J］.中国电机工程学报，2010，30（30）：1－6.

［10］Briz F，Degner M W，Lorenz R D.Analysis and Design of Current Regulators Using Complex Vectors［J］.IEEE Trans.Ind.Applicat.，2000，36（May／June）：817－825.

［11］Holtz J.Sensorless Vector Control of Induction Motors at Very Low Speed Using a Nonlinear Inverter Model and Parameter Identification［J］.IEEE Trans.Ind.Applicat.，2002，38（4）：1087－1095.