潜器模型水下自航试验分析方法探讨

朱爱军，应良镁，胡 科，沈泓萃

（中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

自航试验是潜器水下快速性试验方法的重要组成部分，与模型试验结果的外推技术密切相关。从20世纪60年代国内自力更生地创建了潜艇快速性试验研究的基本设施，同时建立了国内第一代水下快速性试验测试技术，包括水下自航试验分析方法[1]，并随着新的测试技术的应用而不断完善沿用至今。随着时间推移，潜器种类不断丰富，研究对象的范围也早已扩展到了鱼雷、特种运载器和潜水器等多种潜器，但主要针对潜艇建立的自航试验方法在应用到其他类型潜器的过程中暴露出了新的问题。有鉴于此，本文结合某潜器快速性模型试验，探讨现有自航试验方法的适用性，并建立新的试验分析技术。

2 水下自航试验相似条件

水下试验如果能够做到完全避免兴波干扰是最为理想的情况，此时几何相似的潜器只要保证雷诺数Rn和进速系数Jb相等就能做到完全动力相似，虽然在深浸水试验系统（相对潜深h/L～1.0）中[2]，傅氏数Fn的影响可忽略不计，但保证雷诺数Rn相等仍然是很困难的，这将导致船模速度过高而难以实现，物理量过大而无法测量，因此水下试验通常要求雷诺数超过临界值。若雷诺数过低，则由于模型流动状态与实船不同，试验结果无实用价值。对于水下阻力试验，我们要求船体长度雷诺数Rnhull>（1.0～2.0）×107，自航试验中在保证船体雷诺数的同时，还需要关注螺旋桨雷诺数，其表达主要有以下两种常用方式：

前者称肯普夫（Kempf）公式，为ITTC推荐规程里的表达形式，国内目前多采用这一公式，敞水试验时的临界雷诺数[3]要求为3×105：后者多见于苏/俄的文献资料中，要求桨的雷诺数大于5×105。两者表达形式虽然不同，但基本原理及结果是一致的，因为（1）式中的C0.75R可用下式[4]表示：

我们以计算系泊状态（VA=0）的雷诺数为准，则（1）式可表示为：

这与（2）式的表达形式完全一致。对比两式，显然（4）式计算的系泊临界雷诺数约为（2）式的3/5，与两式对应的临界雷诺数要求吻合，该临界值对自航试验同样有效。事实上，常用尺度的水下模型试验如果满足船体临界雷诺数的要求，此时螺旋桨的临界雷诺数也基本满足要求。另外在自航试验中由于船体的存在，螺旋桨雷诺数可以在一定程度上被潜器船体边界层所形成的较高的螺旋桨迎流紊流度所补偿，因此自航试验的螺旋桨对临界雷诺数的要求可低于敞水试验。

3 潜器模型水下自航点的确定

我们记对应实船自航点处的强制力z为FD，为了找到实船自航点，文中从最基本的相似原理出发来说明这个问题。我们知道模型试验首先要保证几何相似：

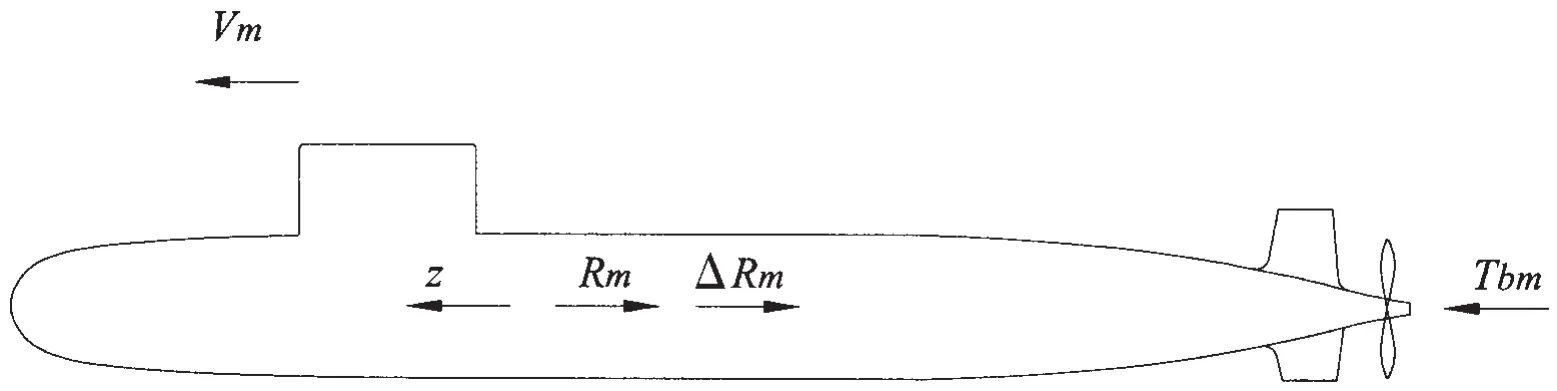
图1 潜器模型自航试验受力示意图Fig.1 Force analysis of an underwater vessel

敞水试验时要保证进速系数相等（运动相似）：

为了能够使模型和实船两个自航系统进行相关，我们还需要使得实桨和模型桨的负荷相似（动力相似），即保证推进器负荷系数相等，由于水下试验不存在同水面舰船一样的傅氏数相似关系，从而缺少了两个系统桨转速之间的直接的对应关系，因此我们采用KT/J02参数来表示桨的负荷，通过简单推导就可得到如下关系：

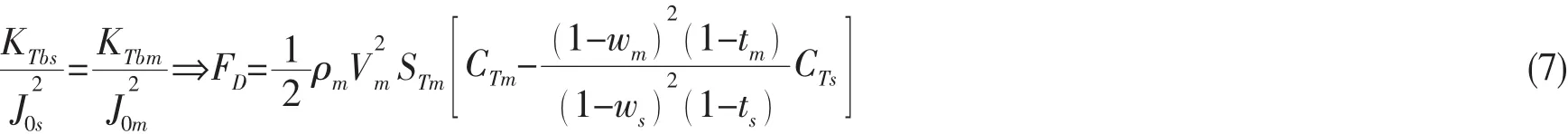
忽略所有尺度效应，上式可简化为：

其物理含义就是当螺旋桨模型发出的推力TBm仅需克服阻力 （Rm-FD），此点即为实艇自航点，相当于实际螺旋桨发出推力TBs克服实船的总阻力Rs。

采用大潜深试验系统时，表面兴波影响可忽略不计，此时（8）式可记为：

事实上受试验条件的限制，我们当前采用的是浅潜深高速试验系统，水下模型深度只能达到水下模型长度的 1/3，常用的模型自航速度范围（2.5～5.5 m/s，Fn=0.40～0.85）恰好在兴波阻力的峰值（Fn≈0.50～0.60）附近，表面兴波较为严重，在满足临界雷诺数要求的情况下，兴波阻力系统可通过模型总阻力系数与摩擦阻力系数和粘压阻力系数的差值计算，此时（8）式应记为：

潜艇试验的统计表明 （Cfs+ΔCT）的数值往往介于Cfm和 （Cfm+Cw）之间，两者的差值小于 0.2×10-3，假设模型试验过程中螺旋桨负荷的小量变化对自航因子的影响不大，因此在潜艇水下试验时可近似认为Fn≈0为自航点，故可以采用超过临雷诺数的自航速度下自航因子的算术平均值作为模型试验自航因子的最终结果。对于潜艇来说，这种简化处理方法虽然并不严格，但可以满足工程预报的要求，因此这种简化方法一直在潜艇的水下自航中沿用至今。但对于除潜艇外的其他水下潜器而言，强制力接近零这一简化条件并不总是成立的，此时模型试验过程中的表面兴波（Cw）和实船的综合补贴取值（ΔCT）就会影响自航点的确定，进而影响自航因子尤其是推力减额。

4 兴波干扰对水下自航点及自航因子的影响

对于本文研究的潜器对象而言，受雷诺数和设备量程的限值，自航速度取为2.1～2.9 m/s。若按照潜艇将模型自航点取为实船自航点，亦即FD=0，此时自航因子计算结果见图2。显然自航因子随自航速度的变化并不明显，这一点在伴流分数和相对旋转效率的两个物理量上尤其明显。同时在潜艇的实艇预报过程中，关注的重点是10 kns以上的中高速的功率性能预报，此时阻力系数虽然仍会随着雷诺数的增大而有所减少，但幅度不到0.15×10-3（主要是摩擦阻力的改变），因此自航因子趋于稳定的常值，采用由试验得到的一组固定值进行计算完全可以满足工程计算的精度要求。

但对于潜器来说，一方面，最高速度往往在10 kns左右，全速度区间内的阻力系数减小幅度达到（0.5～1.0）×10-3，此时推进器负荷显著改变，自航因子尤其是推力减额会有相对明显的变化。另外就是模型试验过程中表面兴波的影响，就本文研究对象而言，若没有表面兴波干扰，阻力系数曲线将如图3中虚线所示，显然受水池试验条件限制从2.5 m/s开始兴波阻力逐渐显现，至3.7 m/s附近兴波阻力达到峰值，事实上从图2中可以看出2.9 m/s处的推力减额已经略有降低，其原因就是该点兴波阻力已经较为明显而在确定自航点时又未计入强制力所致。因此对于低速的潜器水下自航试验来说，自航因子的分析过程理应考虑兴波和负荷的影响，有必要对不同航速下的自航点进行计算修正，这个修正同时包括了模型试验过程中的Cw和实艇雷诺数对Cfs的影响。

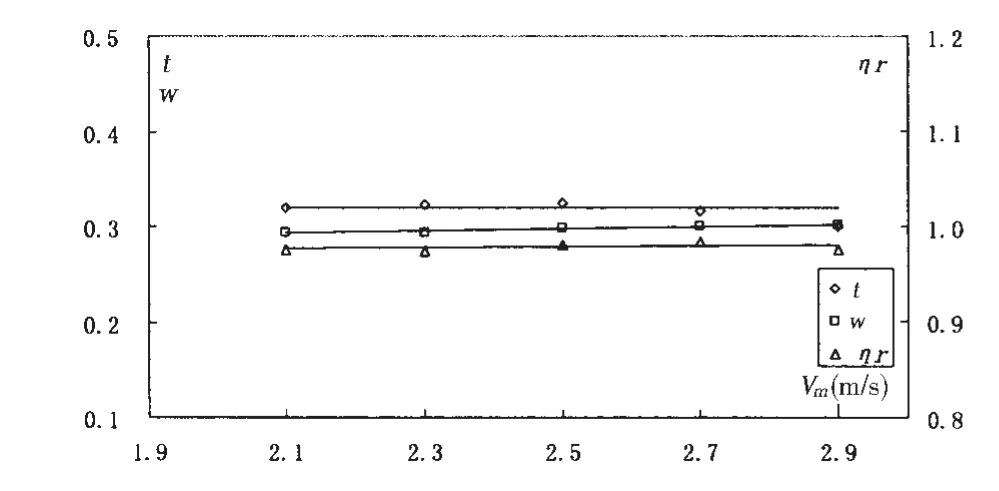
图2 自航因子曲线（强制力为零）Fig.2 Self propulsion factors curves(FD=0)

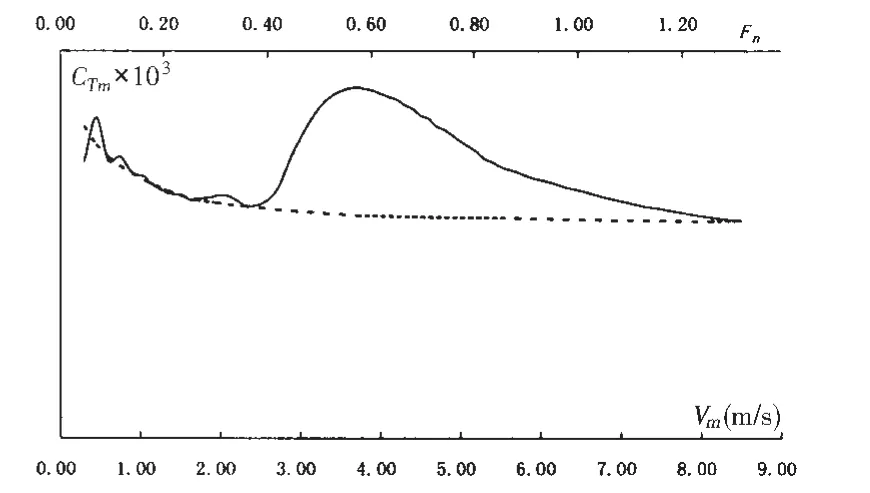
图3 模型阻力系数曲线Fig.3 Model resistance coefficient curve

以实艇5 kns为例，按照算术平均的方法，暂不考虑综合补贴（ΔCT=）0 按照（10）式重新计算自航因子如图4所示，虽然自航速度范围内阻力系数有所变化，但考虑兴波影响后的自航因子尤其是推力减额更加稳定，这也验证了前文螺旋桨负荷的小量变化对自航因子影响不大的假设，采用各模型速度下的自航因子进行算术平均的方法仍然可行。

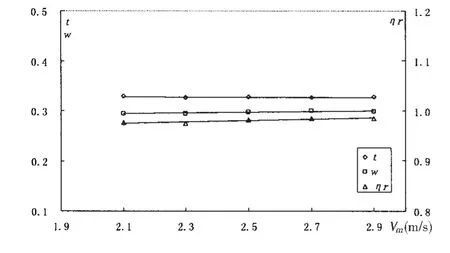
图4 自航因子曲线（强制力不等与零）Fig.4 Self propulsion factors curves(FD≠0)

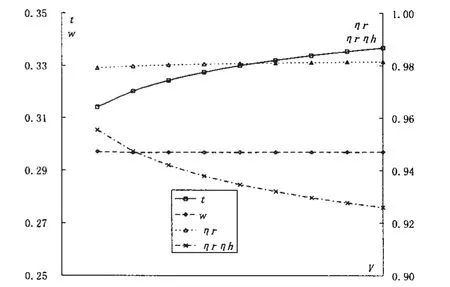
图5 自航因子随着航速变化曲线Fig.5 Self propulsion factors curves along with speed

由于潜器的速度一般较低，超过临界雷诺数的速度范围内，摩擦阻力计算结果相差就达到0.7×10-3。同样令ΔCT=0，计算低速区间内的自航因子，从图5中可以看出相对旋转效率、伴流分数随航速改变的幅值极小，但推力减额随着航速的增加明显上升的趋势。由于推力减额与螺旋桨有效负荷系数σe=T/（0. 5ρV2A）有关，而σe可表示为：

对于以粘性阻力为主的水下潜器而言，随着航速和雷诺数的增大，阻力系数随之越小，而推力减额必然越高。当雷诺数较大阻力系数减小缓慢时，推力减额最后趋于稳定常量，此时即为我们常见的中高速潜艇自航因子预报情况。

5 全负荷自航试验曲线的应用

进行模型自航试验的目的是要提供一组与实船相似的相互影响系数曲线Fi（Jb），其中Jb是船后螺旋桨的进速系数，原则上是可以做到模型试验同实船的Jb相等。对于潜艇由于模型试验和相应的实船建造较多，通过相关分析，我们可以相对准确地知道由于诸多原因造成的阻力补贴系数，但对于一些特种潜器，我们的参考资料不多，阻力补贴系数的取值就存在较大的误差，一旦出现阻力补贴系数与估计值存在较大的出入，此时按（10）式计算的自航点可能会跳出试验范围，进而影响自航点和自航因子的确定。本文研究对象就属于这种情况，因此做一个备用负荷变化较大时的Fi（Jb）曲线是有必要的，这条曲线就是我们所说的全负荷自航试验曲线（或者说船后特性曲线），完成它只是增作一个速度范围变化较大的相互作用系数曲线。

由于全负荷自航试验是通过等转速变车速来实现的，不能够像强迫自航一样通过强制力z建立模型系统和实艇系统之间的关系，但我们仍然可以通过KT/J02这一负荷关系相等来推导两个相似系统间的联系：

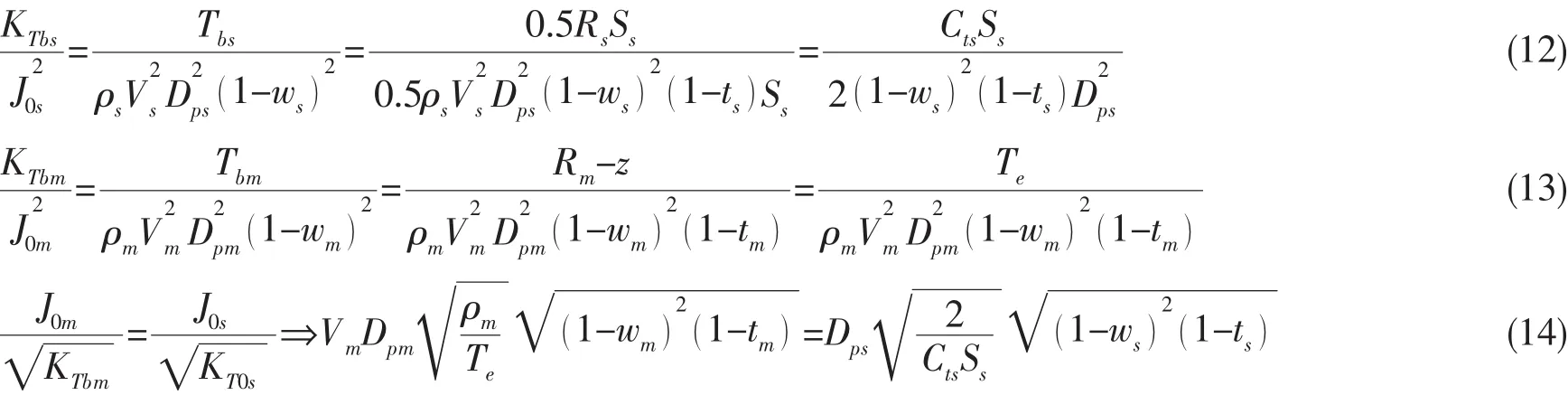
同强迫自航计算自航点处强制力简化方式一样，我们忽略所有尺度效应，并记：

通过前面的分析可知，当模型/实船阻力综合补贴系数不确定时，艇后特性试验可以弥补强迫自航试验范围狭窄的缺陷。通过计算不同阻力综合补贴系数下的自航因子我们可以得到自航因子随阻力综合补贴系数的变化规律见图6。显然相对旋转效率、伴流分数随补贴系数改变的幅值极小，亦即ηr和w对负荷并不敏感，但推力减额随着补贴值或者说螺旋桨负荷系数的增加而减小，由此引起总的船桨干扰因子是增加的，这一结论与上节一致。

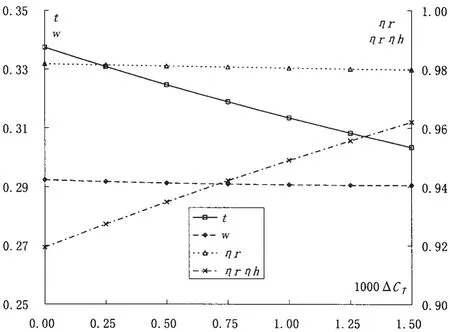
图6 自航因子随阻力补贴值的变化曲线Fig.6 Self propulsion factor curves along with ΔCT

6 无兴波干扰自航试验分析方法的初步探讨

无论是强迫自航方法，还是全负荷自航试验，都没有能够完全避免模型试验状态表面兴波的干扰，其对艇体阻力的干扰我们已经通过强制力或者隐含在负荷系数中进行修正。但无论如何，从试验设计的角度我们希望能够尽可能不出现兴波干扰这一不确定因素。由此我们可以如此描述潜器水下自航试验的要求：能够覆盖尽量大的Jb范围；同时应尽可能地避开兴波干扰。按照这一要求结合上文介绍的两种自航试验方法我们提出一种新的水下自航试验方法。

对于Jb较低的区间，采用nm=const的全负荷自航试验，为了保证低航速时螺旋桨有较高的雷诺数转速应较高，此时车速应满足傅氏数小于0.40，以避免兴波干扰，此后的实验点将处于兴波影响的区域内（如图3所示）。在Jb较大的区间，我们采用Vm=const的强迫自航试验，车速的选择也应保证Fn小于0.40，通过改变螺旋桨转速来调整Jb，当KTb较小时螺旋桨的转速较低，本身的雷诺数Rn较低，但可以认为被艇体模型边界层所形成的较高的螺旋桨迎流紊流度所补偿。两种试验方法得到的试验点应该有一定程度的吻合。按照上述原则，我们将试验数据按有无兴波干扰分成两个子样群，分析表明有兴波干扰时推力、扭矩系数方差是无兴波干扰时的2倍以上，测量值与期望值之间的差异更是接近2%，因此无兴波干扰曲线的数据点离散程度较小，对提高试验精度有利。

图7 无兴波干扰Fi（Jb）曲线Fig.7 Fi（Jb）curve without wave resistance

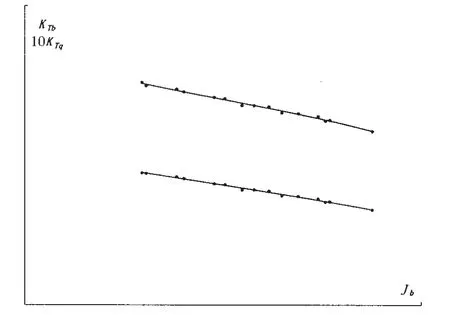
图8 有兴波干扰Fi（Jb）曲线Fig.8 Fi（Jb）curve with wave resistance

以这些样本为基础，假设ΔCT=0按照（15）式计算自航因子（见图9）。从数值上看，有无兴波干扰的伴流分数和相对旋转效率相差不到1%，已在试验误差之内。有兴波干扰时推力减额虽然数值上略高，最大差异也仅在2%左右，亦即由兴波引起螺旋桨负荷增加并不会引起自航因子的显著改变，这与前面的分析结论一致。

7 结 论

图9 有无兴波影响的自航因子对比Fig.9 Comparason of self propulsion factors

本文在模型自航试验原理的基础上，分析了针对低速潜器强迫自航试验自航点的确定和修正方法；考虑到部分潜器在准确确定模型/实船阻力附加值上存在较大难度，文中提出了船后全负荷自航试验方法，并分析得出自航因子随阻力补贴值的变化规律；进而在以上两种试验方法的基础上，进一步探讨能够完全避免兴波干扰的试验方法，并对试验数据进行了对比分析。综合以上研究，我们得到主要结论如下：

（1）在部分潜器的自航试验中，当 （Cfm+Cw）与Cfs的差值与 ΔCT接近时，近似认为FD≈0为自航点进行数据分析一般不会引起自航因子较大的预报误差，但在全航速段尤其是低速段的实船预报中采用同一自航因子值尤其是推力减额是不尽合理的，这只是一种工程近似分析方法，完全可以通过强制力来修正兴波干扰的影响。

（2）由于强制力的计算和阻力附加值有很大的关系，当阻力附加值难以被准确确定时，建议在强迫自航试验的基础上补充全负荷自航试验曲线，可以弥补强迫自航试验范围狭窄的缺陷。两种试验方法的原理是一致的，常规的强迫自航试验可以看作是较窄范围内的全负荷自航试验曲线的特例。

（3）不同阻力附加值下的自航因子计算表明，伴流分数和相对旋转效率对负荷并不敏感，但阻力附加值越大，螺旋桨负荷越重，推力减额越小，但总的船桨干扰因子是增加的。

（4）本文结合两种自航试验方法探讨了一种避免兴波干扰水下自航试验方法，从试验数据点分布来看，采用这种方法得到的试验数据离散程度更小，有利于提高试验精度。

[1]CB/Z 216-87.潜艇船模水下阻力、自航试验规程[S].北京:中国船舶工业总公司指导性技术文件,1987.

[2]王锡良.关于潜艇水下快速性试验若干问题的探讨[J].舰船性能研究,1983(1):1-10.

[3]CB/T 346-1997.螺旋桨模型敞水试验方法[S].北京:中华人民共和国船舶行业标准,1997.

[4]胡志良译.经计算机进一步分析过的瓦赫宁恩B系列螺旋桨资料[J].江苏船舶,1993(2):33-42.

[5]Beveridge J L.Propulsion characteristics of a submerged model as affected by Reynoldes number[M].PB153919,1960.