关于拉格朗日方程应用中的问题讨论
2012-09-20刘喜斌
刘喜斌
(湖南理工学院 物理与电子学院, 湖南 岳阳 414006)
关于拉格朗日方程应用中的问题讨论
刘喜斌
(湖南理工学院 物理与电子学院, 湖南 岳阳 414006)
拉格朗日方程是分析力学中一个极为重要的方程. 本文总结了在应用拉格朗日方程解题时应注意的几个问题,并结合实例加以分析讨论.
拉格朗日方程; 动能; 势能; 广义力
拉格朗日方程是分析力学中一个极为重要的方程, 它是以s为广义坐标q1,q2,…,qs作为独立变量的二阶微分方程组, 对于受理想、完整约束的一般力学体系, 它具有以下形式:
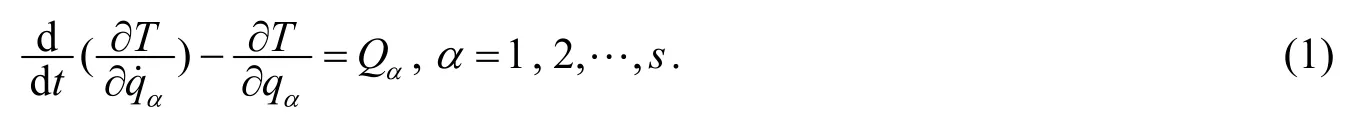
其中T为动能,Qα为广义力.
当主动力为有势力时, 它的形式为:
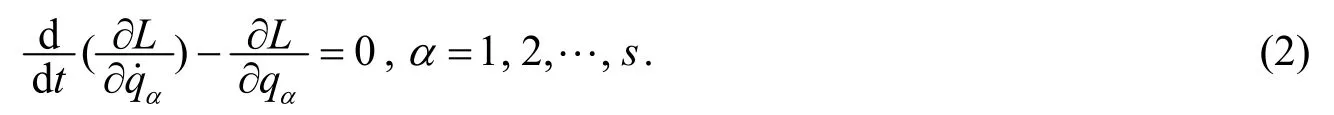
在应用它解题时, 必须弄清以下两点:
2.掌握广义力的概念及其计算公式, 以及明确全导数与偏导数的运用也是应用拉氏方程的前提.
例1 质量为M的滑块受水平力的作用, 沿倾角为α的光滑固定斜面滑动, 滑块上铰接一长为l, 质量为m的匀质直杆,铰接处光滑. 此系统只能在铅垂面内运动. 试用拉氏方程建立系统的运动微分方程.
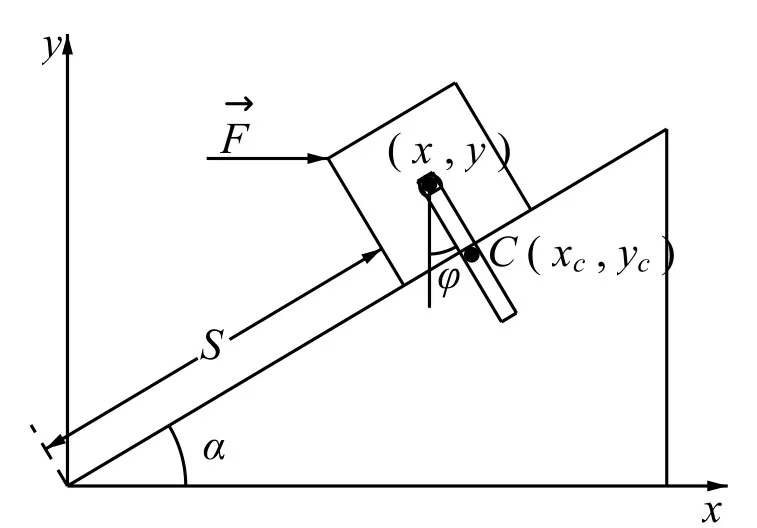
图1
分析以滑块与直杆构成一系统, 自由度为2, 取s和φ为广义坐标(图1), 此系统受理想、完整约束.主动力mg、Mg、因为不是有势力, 所以用方程(1).
1° 求动能表达式
系统的动能=滑块的动能+直杆的动能. 滑块只做平动, 直杆随滑块平动, 且有转动, 其动能可由柯尼希定理给出, 所以系统动能为:
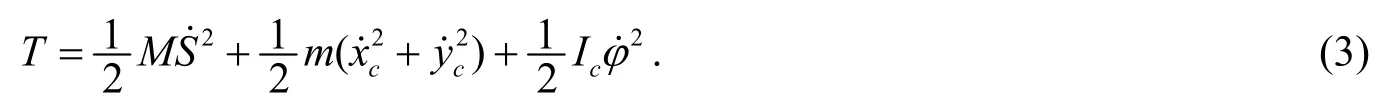
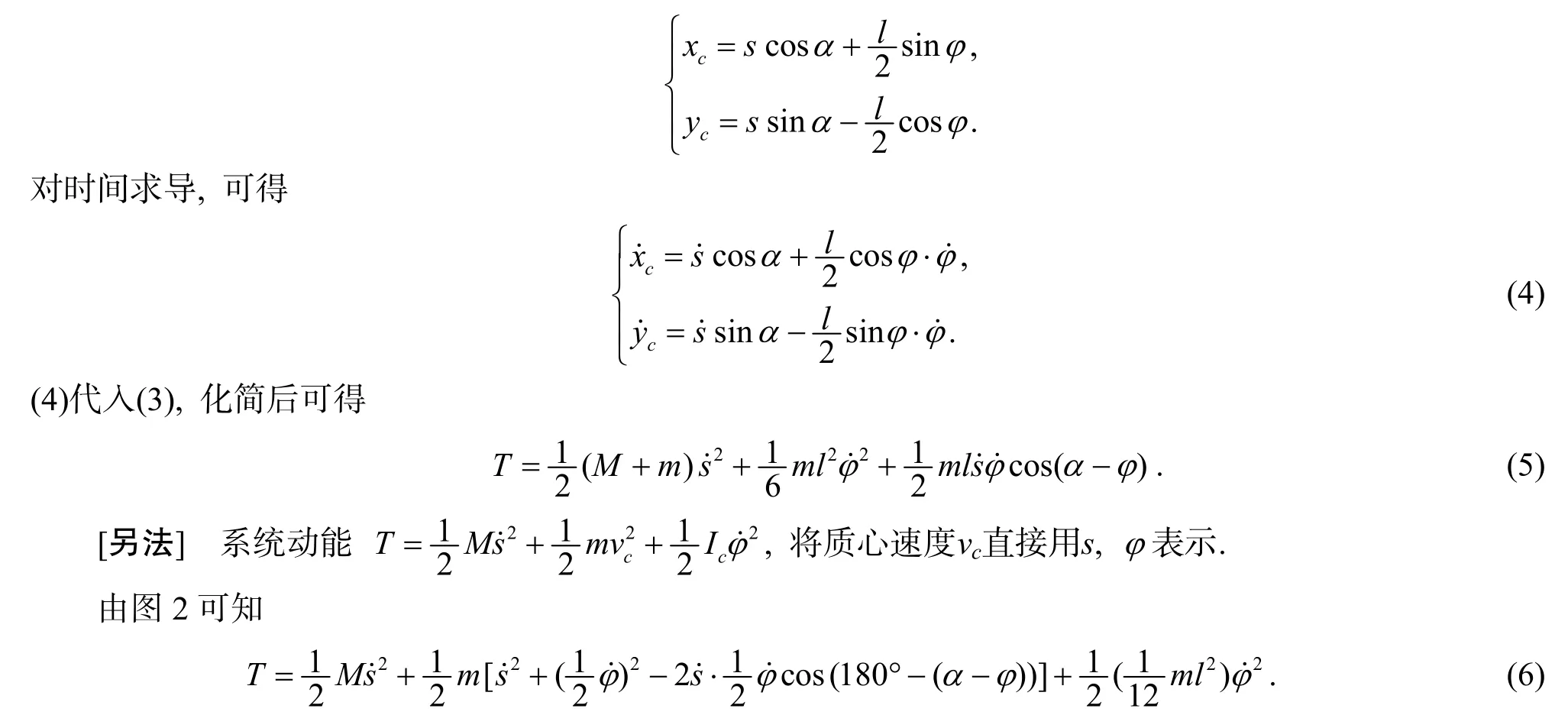
(6)式化简后与(5)相同.
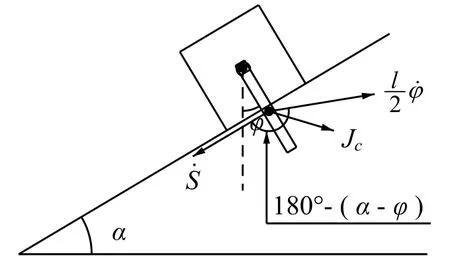
图2
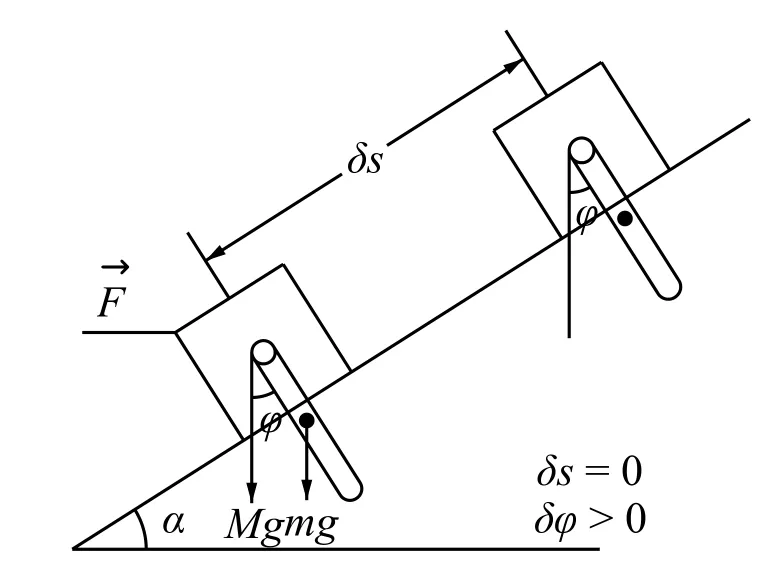
图3
2° 求广义力
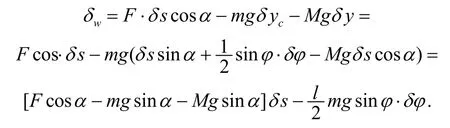
所以有
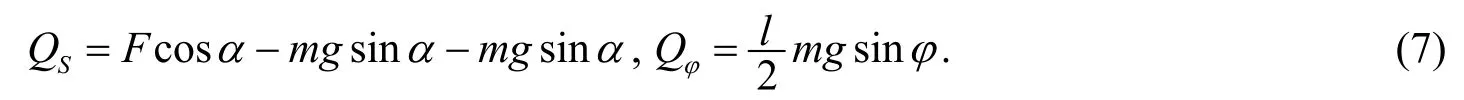
[另法] 由的独立性, 也可以分别计算:
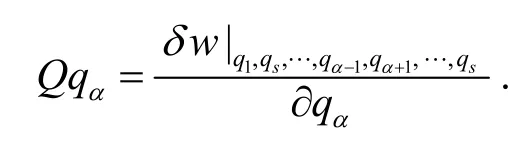
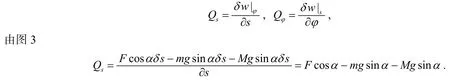
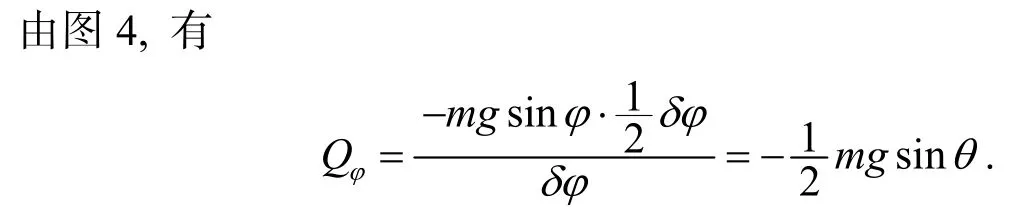
当然, 还可以根据广义力的定义式:

来计算, 不过这种方法不如前两种方法灵活简便. 由上可知,广义力的计算及概念的理解是很关键的.
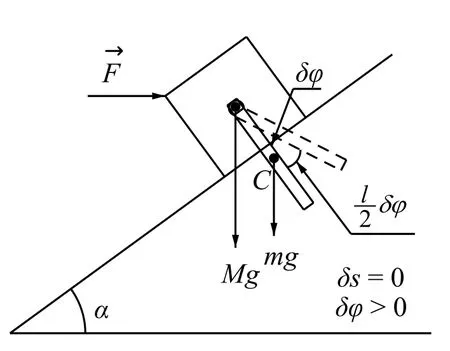
图4
3° 代入拉氏方程进行运算. 运算时, 有许多初学者往往由于不能正确进行全导数和偏导数的计算而得不出正确的运动方程.
对于广义坐标s:0
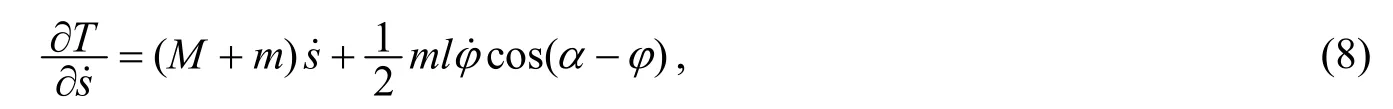
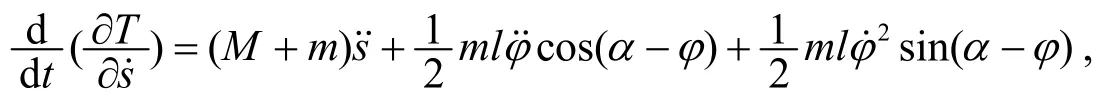
(注意, 这是对t求全导数, (8)式右端所有随时间变化的量都是对t求导)
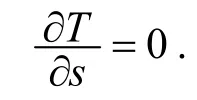
再考虑到(7)式, 关于广义坐标s的拉氏方程为
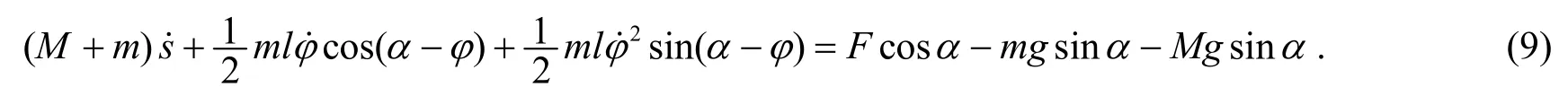
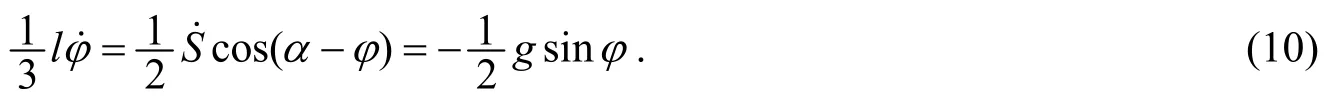
由(9)式我们可以看出, 此方程就是质点组相对惯性系的动量定理在s方向上的分量式, (9)式后端的广义力即为s方向上所有主动力的投影. 而(10)式可以写成

例2 质量为M的滑块与质量为m的小球系于轻绳的两端, 滑块放在光滑的水平面上, 绳子跨过不计质量的定滑轮, 如图5所示. 开始时, 使小球偏离一小角度, 然后自由释放. 设绳子不可伸长, 试用拉格朗日方程写出此系统的运动微分方程.
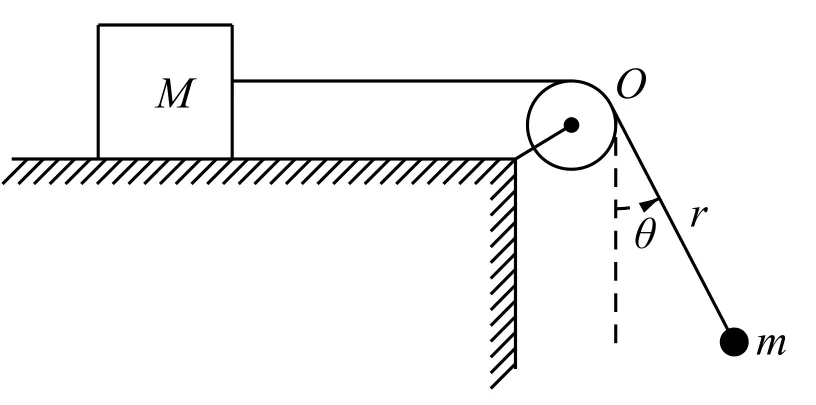
图5
分析滑块与小球构成一个系统, 自由度为2. 如果r和θ确定了, 系统便被完全确定, 故取r和θ为广义坐标.系统受主动力Mg和mg, 是有势力所以用式(2)形式的方程. 由方程(2)可知, 拉格朗日函数对系统的运动规律起决定一切的作用, 因为拉氏函数能反映出系统的许多信息: 从动能表达式可以反映系统是由什么样的质点和刚体构成; 从势能表达式可以反映系统内部及其与外部相互作用的情况; 是否存在循环坐标, 从而断定那些与循环坐标相应的广义动量守恒; 从拉氏函数不显含时间t, 从而断定相应的广义能量守恒, 当然, 这时系统机械能是否守恒还必须看坐标变换方程是否显含时间t, 如此等等, 所以拉氏函数被称为系统的特征函数.
1° 求动能表达式.
系统的动能等于滑块的动能加小球的动能, 故总动能为
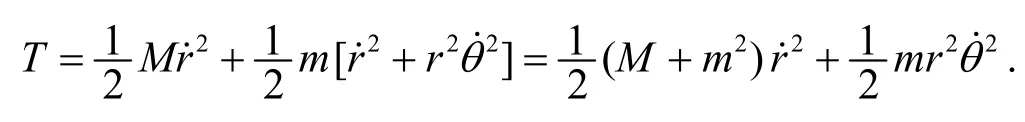
2° 求系统的势能.
取0点为零势点, 则系统势能为
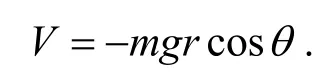
3° 构成拉氏函数.
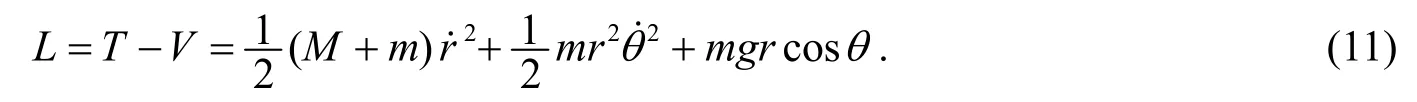
将(11)代入方程(2)即可. 这里同样也是两种导数的计算问题. 化简后可得:

以上两个例题是侧重于运动微分方程的正确得出, 以及在解方程中须注意的问题, 所得出的都是高阶微分方程组, 即使给出初始条件, 要解这些方程组仍有一定难度, 尤其是例1. 下面再给一个例题, 这是一个二阶微分方程, 解这一个方程就方便得多.
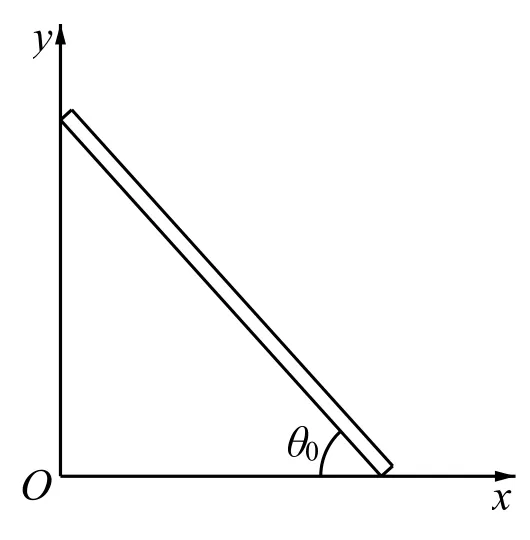
图6
例3 长为l的均匀直杆AB, 其端点沿光滑的直线导槽ox及oy滑动,开始时杆与水平成0θ角, 杆由静止开始滑动, 试用拉格朗日方程求杆着地时的角加速度和角速度.
分析因为杆长一定, 此杆只须一个量θ确定其位置, 故取θ为广义坐标. 杆受主动力mg, 是有势力. 杆的动能可由柯尼希定理写出; 若以x轴为零势面, 则可写出其势能. 故拉氏函数的构成可写为
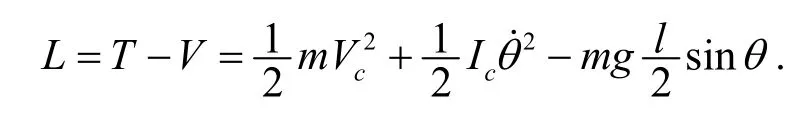

着地时, 0θ=, 由(14)、(15)式便可得出所求的角速度和角加速度.
[1] 周衍柏. 理论力学教程[M]. 北京: 高等教育出版社, 1999
[2] 周培源. 理论力学[M]. 北京: 人民教育出版社, 1953
About Discussion Problems of the Application of Lagrange Equation
LIU Xi-bin
(College of Physics and Electronics, Hunan Institute of Science and Technology, Yueyang 414006, China)
Lagrange equation is an important equation in analytical mechanics. This paper summarizes some problems which should be paid attention to when use the Lagrange equation, and analyze and discuss based on the examples.
Lagrange equation; kinetic energy; potential energy; generalized force
O175.2; O313.3
A
1672-5298(2012)02-0037-05
2012-03-16
刘喜斌(1963- ), 男, 湖南华容人, 硕士, 湖南理工学院物理与电子学院副教授. 主要研究方向: 光电子与物理教学
