GA-凸函数的若干不等式
2012-09-20时统业
时统业, 吴 涵
(海军指挥学院 浦口分院, 江苏 南京211800)
GA-凸函数的若干不等式
时统业, 吴 涵
(海军指挥学院 浦口分院, 江苏 南京211800)
利用GA-凸函数的定义和性质, 得到两个不等式, 它们是已有的GA-凸函数的Hadamard型不等式的加细.
GA-凸函数; Hadamard型不等式; 加细
引言与引理
定义1[1]设是定义在区间上的连续函数, 如果对于任意有

许多文献([如[2]、[3]、[4])给出下面关于GA-凸函数的Hadamard型不等式.
定理1 设上的GA-下凸函数, 则
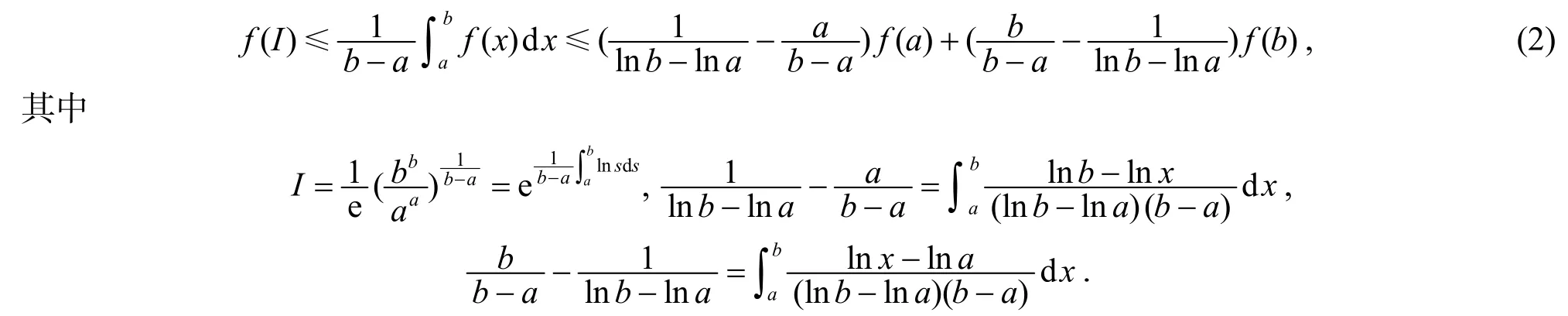
引理1[1]设是定义在上的函数, 则上的GA-下凸函数的充要条件为上的下凸函数.
引理2[5]设上的下凸函数, 则对任意有
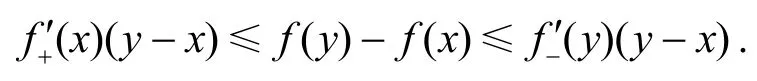
引理3 设是定义在上的GA-下凸函数, 则

证明令那么
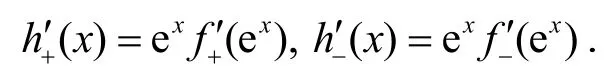

注:记
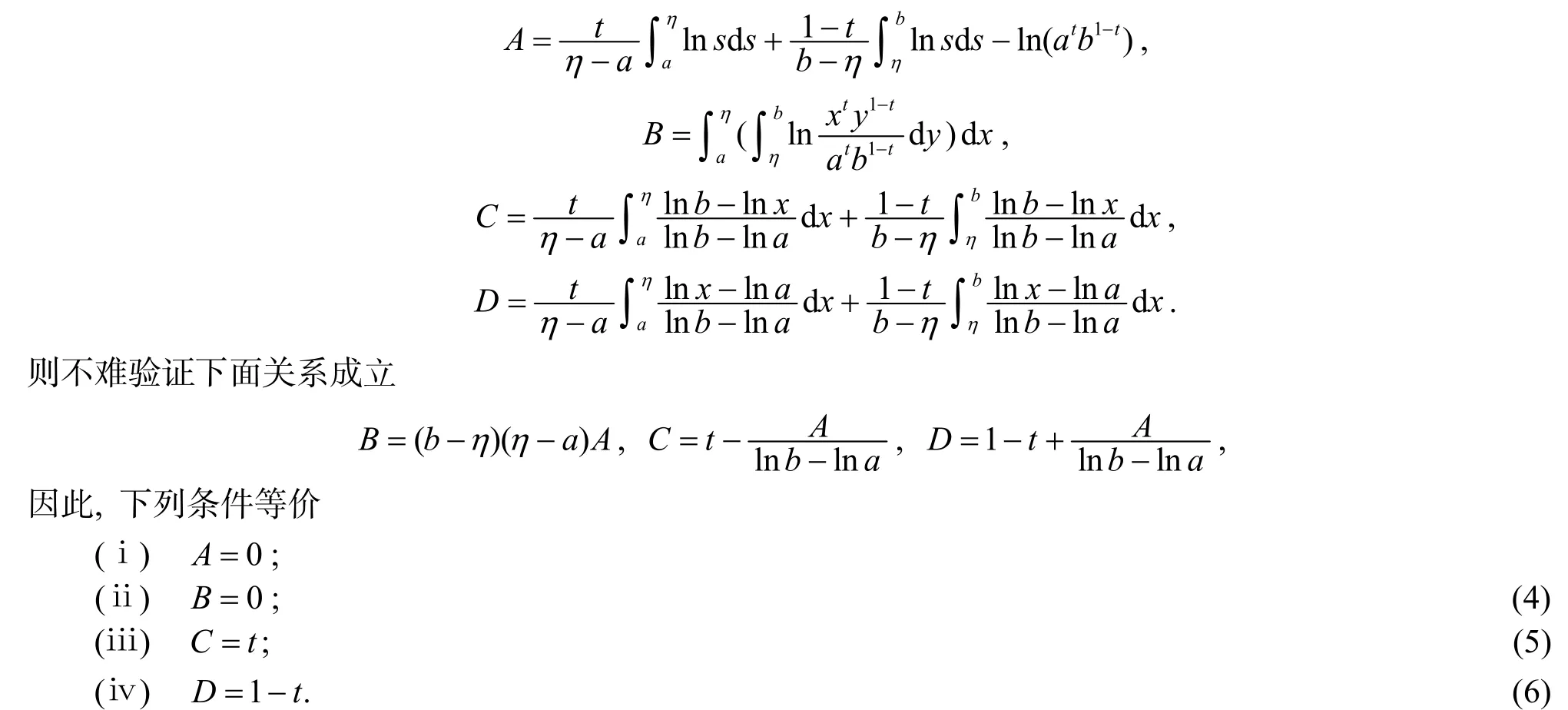
引理5 设上的连续的GA-下凸函数, 则有
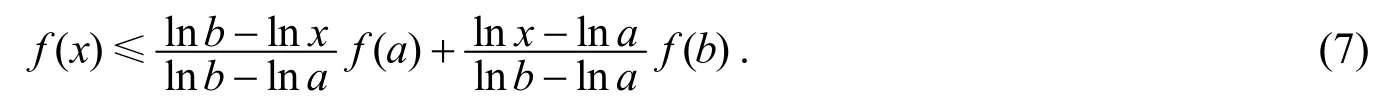
证明对任意有

由GA-下凸函数的定义立得(7)式.
主要结果及其证明
定理2 设上的连续的GA-下凸函数,则
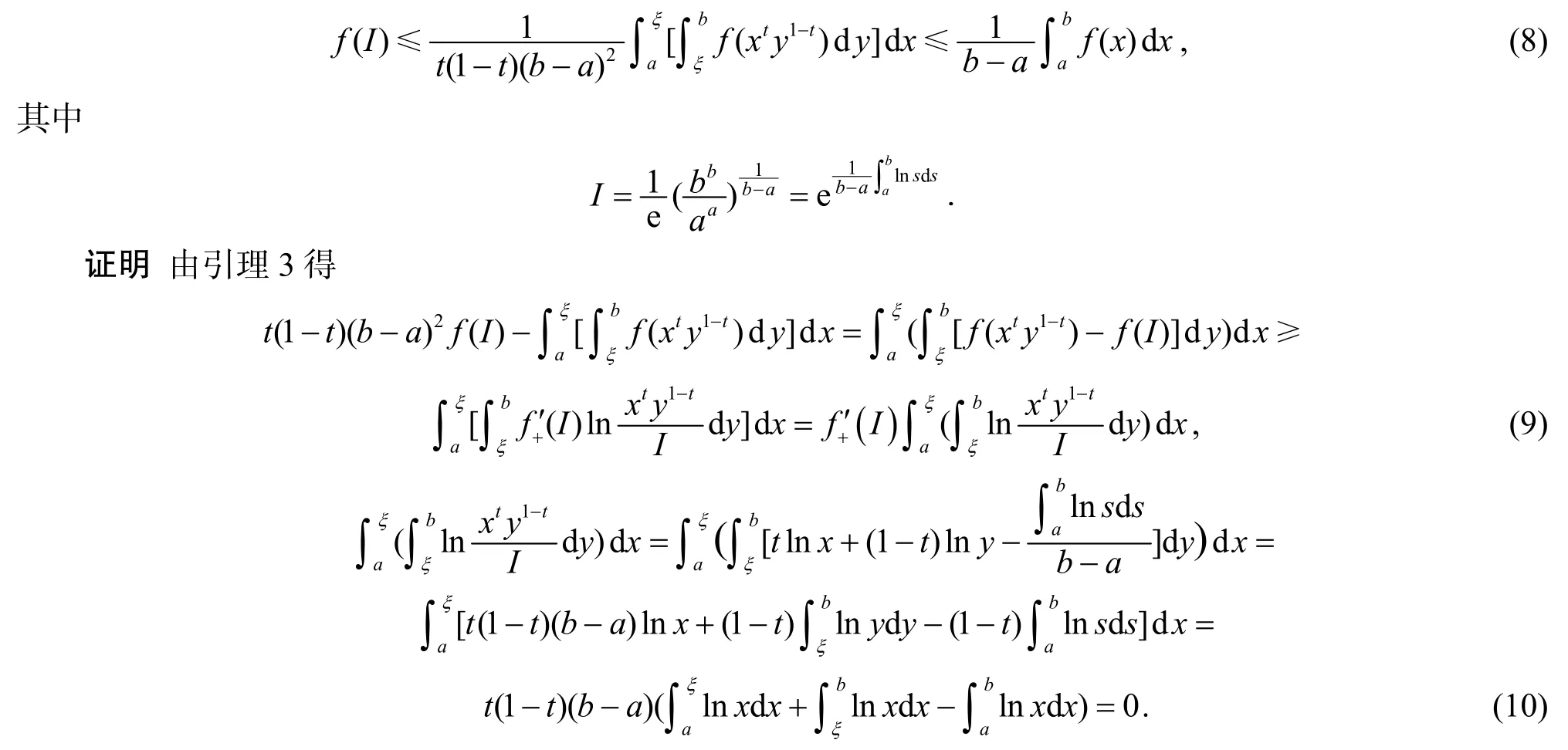
由式(9)和式(10)即可证得(8)式的左端不等式.
由GA-下凸函数的定义得

显然, 定理2给出了(2)式左端部分的一个加细.
推论1 设上连续的GA-下凸函数, 则
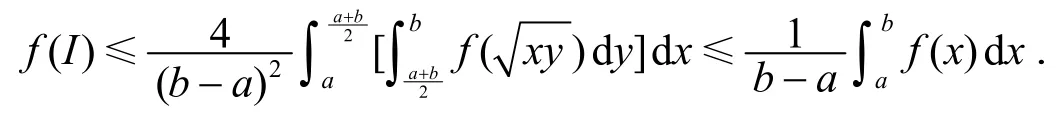
证明在定理2中取立得.
定理3 设是定义在上的连续的GA-下凸函数,满足(3)式, 则有

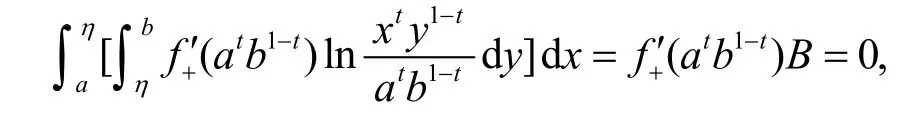
由此证得(12)式的第一个不等式.
由GA-下凸函数的定义得


所以由式(14)、(15)、(5)、(6)得

(12)式的第三个不等式得证.
定理3给出了(1)式的一个加细.
推论2 设上连续的GA-下凸函数, 那么有

证明当满足(3)式, 由定理3即得推论2.
[1] 吴善和. GA-凸函数与琴生不等式[J]. 贵州师范大学学报(自然科学版), 2004, 22(2): 52~55
[2] ZHANG X M,CHU Y M.ADouble Inequality for the Gamma and Psi Functions[J]. International Journal of Modern Mathematics, 2008, 3(1): 23~27
[3] 华 云. 关于GA-凸函数的Hadamard型不等式[J]. 大学数学, 2008, 24(2): 147~149
[4] 张小明, 褚玉明. 解析不等式新论[M]. 哈尔滨: 哈尔滨工业大学出版社, 2009: 198~203
[5] 匡继昌. 常用不等式[M]. 第3版. 济南: 山东科学技术出版社, 2004: 375~376
Several Inequalities for GA-Convex Functions
SHI Tong-ye, WU Han
(Pukou College, Naval Command Institute, Nanjing 211800, China)
Some refinements to Hadamard’s type inequality for GA-convex functions in the existing literature are obtained by using the definition and the properties of GA-convex function.
GA-convex function; Hadamard’s type inequality; refinement
O178
A
1672-5298(2012)02-0007-04
2012-02-15
时统业(1963- ), 男, 河北张家口人, 硕士, 海军指挥学院浦口分院副教授. 主要研究方向: 基础数学
