多项式的友阵及其应用
2012-09-20周立仁
周立仁
(湖南理工学院 数学学院, 湖南 岳阳 414006)
多项式的友阵及其应用
周立仁
(湖南理工学院 数学学院, 湖南 岳阳 414006)
利用多项式的友阵判别两个多项式有无公共根, 从而解决一类多元高次方程的求解问题.
多项式; 友阵; 方程; 根
多元高次方程组是否有解的判定及求解方法都较繁难. 本文利用多项式友阵判别两个多项式有无公共根, 从而较易解决一类多元高次方程组的求解.
定义设数域上的一多项式

称A为的友阵.
定理(Barnett) 设是首一复系数多项式, 且次数均不小于1,A为的友阵, 则非退化.

推论设是次数不小于1的首一复系数多项式,A为的友阵, 则有公共根为退化阵.
由于在定理中f(x)与g(x)的地位是对等的, 故若互换它们的位置, 相应的结论亦成立.
在利用上述结论去判断多项式有无公共根时, 关键一步是计算友阵的方幂. 下面介绍当幂指数k不超过友阵A的阶数n时, 求的一种简易方法, 其步骤为先求出Ak的第1列, 再由第1列推出第2列, 再由第2列推出第3列,, 直至推出第n列.

其中α是A的末列向量. (4)式给出了kA的第1列的求法.
例1 解方程组

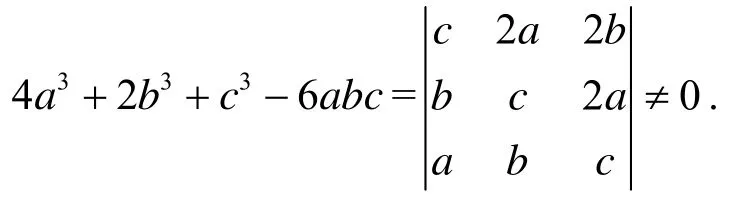
[1] 杨家骐, 王卿文. 高等代数在初等数学中的应用[M]. 北京: 高等教育出版社, 2003
[2] 北京大学数学系几何与代数教研室前代数小组. 高等代数[M]. 第3版. 北京: 高等教育出版社, 2003
Polynomial Companion Matrix and It’s Applications
ZHOU Li-ren
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)
A class of multivariate higher order equations was solved by using polynomial companion matrix to judge that whether two polynomials have common roots or not.
polynomial; companion matrix; equations; root
O151.2
A
1672-5298(2012)02-0014-03
2012-03-25
周立仁(1959- ), 男, 湖南湘阴人, 湖南理工学院数学学院副教授. 主要研究方向: 矩阵理论及应用
