基于拉氏变换的常系数线性微分方程的初值问题

赵小玲

（上海电机学院文理学院，上海 201306）

拉普拉斯变换是一种具有广泛应用的积分变换。由于拉氏变换及其逆变换有一些简洁明了易于计算的性质，在各领域都有着广泛的应用。而运用拉氏变换的性质去解决较复杂的常系数非齐次线性微分方程的初值问题也成为解这一类特殊微分方程的好方法。

1 拉普拉斯变换的定义和性质

拉氏变换的几个主要性质在实际应用中都很重要。这些性质都可由拉氏变换的定义及相应的运算性质加以证明。

性质1表明，函数的线形组合的拉氏变换等于各函数的拉氏变换的线形组合。此性质也可以推广到有限个函数的线形组合的情形。

性质2表明，像原函数乘以后所做拉氏变换的像函数，等于其原先像函数作平移，因此性质2称为平移性质。

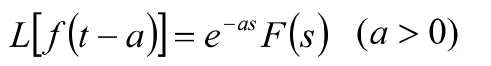
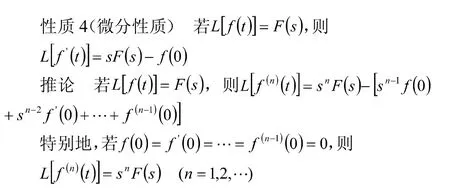
性质4表明，一个函数求导后取拉氏变换，等于这个函数的拉氏变换乘以参数s再减去这个函数的初值。这使得我们有可能将的微分方程的初值问题化作的代数方程。此性质还可以推广到函数的 阶导数的情形。因此性质4在解微分方程中有重要作用。

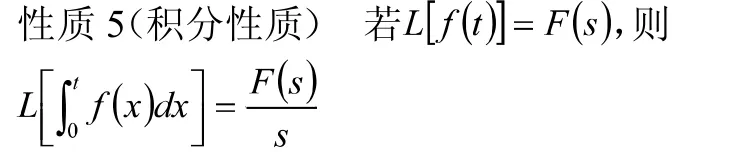
与性质4相对应，性质5表明一个函数积分后取拉氏变换，等于这个函数的拉氏变换除以参数。性质5也可以推广到有限次积分的情形

2 拉氏变换的逆变换

在求像原函数时，常从拉氏变换表中查找，同时要结合拉氏变换的性质。因此把常用的拉氏变换的性质用逆变换的形式列出如下。

在用拉氏变换解决工程技术中的应用问题时，经常遇到的像函数是有理分式。一般可将其分解为部分分式之和，然后再利用拉氏变换表求出像原函数。

3 微分方程的拉氏变换解法

在解决常系数非齐次线性微分方程的初值问题时，若运用微分方程的一般解法，首先要求出常系数非齐次线性微分方程所对应的齐次线性微分方程的通解和非齐次线性微分方程本身的一个特解，得到非齐次线性微分方程的通解。然后代入初始条件，求出通解中的常数，从而得到常系数非齐次线性微分方程满足某种初始条件的特解。整个解题过程略显繁杂。

而利用拉氏变换解常系数非齐次线性微分方程时，则在对微分方程作拉氏变换的过程中就考虑了初始条件，得到的就是满足这个初始条件的特解，相对比较简洁。其具体步骤如下：常系数线性微分方程作拉普拉斯变换（考虑到初始条件），得到像函数的代数方程；解代数方程，得到像函数并分解成部分分式之和；利用拉氏变换表求出像函数的拉普拉氏逆变换，得到像函数的原函数，即微分方程的特解。

用一般的微分方程的解法：

即为原方程满足初始条件的特解。

用拉氏变换解线性微分方程，在求解过程中就考虑了初始条件，得出的就是满足题设初始条件的特解，很简洁。可见，在解决常系数线性微分方程的初值问题时，用拉普拉斯变换法是一种非常简便有用的方法。