串列钝体驰振气动干扰效应的数值分析

李胜利 路 毓 王东炜

(郑州大学土木工程学院，郑州 450001)

串列钝体驰振气动干扰效应的数值分析

李胜利 路 毓 王东炜

(郑州大学土木工程学院，郑州 450001)

为了研究不同数量、不同断面形式串列钝体的驰振气动干扰效应，以某大跨径悬索桥桥塔为例，采用CFD数值分析方法研究了双幅桥塔的4个塔柱在4种断面情况下的驰振气动干扰效应，并将其与单幅桥塔的2个塔柱在同样4种断面情况下的驰振气动干扰效应进行了比较分析.结果表明:当双塔柱矩形断面位于双塔柱倒直角断面桥塔上游或双塔柱倒外凸圆弧断面位于双塔柱倒直角断面下游时，可能发生驰振;对于单幅桥塔的2个塔柱，下游塔柱主要在0°风攻角附近发生驰振，且随着2个塔柱间间距的减小发生驰振的可能性增大;对于双幅桥塔的4个塔柱，由于气动干扰效应的存在，第4个塔柱不易发生驰振，在矩形断面和倒外凸圆弧断面情况下，第2，3个塔柱可能发生驰振失稳.

串列钝体;驰振;气动干扰效应;CFD;数值模拟

为了满足日益增长的交通量，在高速公路的旧桥附近新建一座相似的桥梁或者在新建时建成双幅桥的情况越来越多，如2004年建成的新塔科马桥为1950年建成的塔科马桥附近新建的桥梁，广州平胜大桥和青岛海湾大桥则为直接建成的双幅桥.对于双幅桥塔，塔柱间存在气动干扰效应，施工期桥塔的驰振性能值得研究.

驰振是由于负气动阻尼引起的几乎垂直于风向的结构振动，常出现在具有特殊截面形状(如D形截面)的细长结构中，最早是由登哈托在研究裹冰电缆时发现的，并提出了登哈托判据［1］.随后，有学者采用风洞实验的方法对覆冰三分裂导线的三分力系数和驰振力系数进行了研究［2］.在对覆冰电缆研究的基础上，研究者对三角形截面的驰振稳定性进行了研究［3］.随着CFD技术的发展，学者们采用数值方法研究了带有临界截面的矩形柱体的低频驰振［4］，并结合具体工程对桥塔的驰振临界风速公式进行了探讨［5］，研究了桥塔施工期暂态结构的驰振性能［6］，对不同断面桥塔的气动性能进行了优化［7］.研究结果表明，采用倒角截面形式可以不同程度地改善桥塔的气动性能;例如，明石海峡大桥采用的十字形断面塔柱可以改善其气动性能［7］.由于塔柱群体间距离较近，塔柱间存在气动干扰效应，单个塔柱的驰振性能必定会受到影响［8］.因此，矩形断面、倒直角断面、倒内凹圆弧断面和倒外凸圆弧断面塔柱群的驰振性能优劣有待研究.

本文以某大跨径悬索桥桥塔为例，采用CFD方法，考虑塔柱群体间的气动干扰效应，研究了双幅桥不同断面上4个塔柱的驰振性能，为双幅桥塔塔柱断面形式的选择提供理论依据.

1 阻力系数和升力系数的数值计算

根据登哈托判据可知，驰振力系数的计算是桥塔驰振性能分析的必要条件.这种计算是以阻力系数CD和升力系数CL为基础的，其计算公式如下:

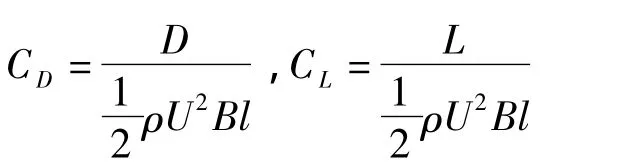
式中，D和L分别为风轴坐标系下塔柱断面受到的气动阻力和升力;ρ为空气密度，取值为1.225 kg/m3;U为平均风速;B为特征尺寸;l为节段模型的长度.

数值风洞模型采用不可压雷诺时均N-S方程中的标准k-ε双方程湍流模型.由于横风向空气流速较低，可按二维定常不可压流动状态考虑，同时忽略温度变化的影响，静力计算时按定常流动状态处理［9］.

利用计算流体动力学软件Fluent 6.1.2模拟模型周围流场，主要参数的设置方法如下:采用有限体积法模拟雷诺数在亚临界区域的绕流流动，利用二阶迎风格式离散控制方程，利用标准壁面函数法处理近壁面边界条件，且对流项和扩散项均按二阶精度考虑;采用默认的Simple算法解决动量方程中速度分量和压力项耦合的问题;计算域的长和宽的取值均大于模型特征长度的40倍.由于悬索桥桥塔塔柱截面明显钝化，流场分离点位置几乎不变，在一般的工程结构所涉及的风速范围内，气动力系数与雷诺数无关，故不考虑雷诺数的影响［10］.

数值计算时，为了在湍流边界层获得有效的分辨率，绕流网格划分得很细.但由于桥塔尺寸很大，如采用全尺寸模型计算，网格数量巨大，会导致湍流求解迭代速度很慢［11］.故本文采用

的缩尺比，网格划分采用非结构网格，划分的网格数量约为4.5×106个，内边界最小网格尺寸约为0.1 m.

外边界条件中，流体进口处采用速度入口边界条件，上下边界处采用对称边界条件，流体出口处采用压力出口边界条件.内边界条件均为无滑移边界条件.

表1和图1为采用上述参数设置方法获得的计算结果.图 1 中，CD，S和CL，S分别表示阻力系数和升力系数的实验值［12］，CD，M和CL，M分别表示阻力系数和升力系数的模拟值，α表示风攻角，c表示静风系数.显然，数值计算结果和文献［7］中的结果存在差异，其主要原因可能是所采用的相似比、计算域和单元个数等与文献［7］不同.但由于这种差异较小，且计算结果的趋势与实验值吻合较好，因此可以认为本文所采用的数值风洞参数设置方法具有一定的合理性.

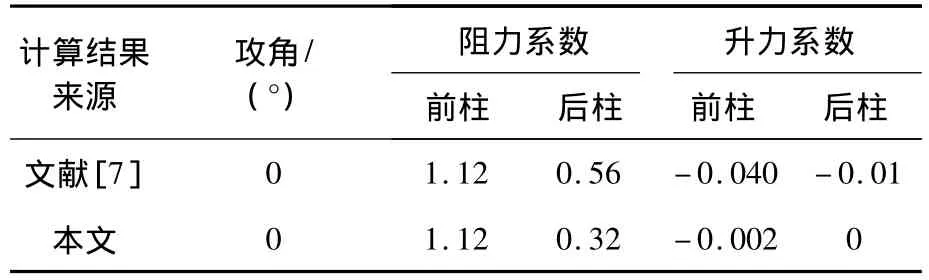
表1 某桥塔塔柱断面的阻力系数和升力系数

2 驰振力系数的数值计算

2.1 驰振分析方法

根据登哈托判据可知，dCL/dα+CD＜0是驰振不稳定的必要条件.将A=dCL/dα+CD称为驰振力系数［6］.多塔柱驰振稳定性研究的核心内容之一即是计算驰振力系数.

图1 不同断面的阻力系数和升力系数

2.2 模型建立

下面以某大跨径悬索桥桥塔塔柱断面的基本尺寸和所处的桥位处风环境为基础，研究双幅桥塔的驰振性能.塔柱断面的尺寸和间距如图2所示.图中，B为特征尺寸.塔柱2和3之间的净间距采用广州平胜大桥主梁净间距［10］.钝体的气动力特性主要依赖从钝体前缘分离的剪切层的变化，故本文通过改变断面形式来控制分离流，从而达到减小风荷载的目的，例如通过改变柱体的倒角形式来减小风阻力［12］.鉴于建筑造型上广泛存在着矩形、倒直角、倒内凹圆弧和倒外凸圆弧断面，故本文在考虑气动干扰效应的情况下，通过改变倒角的形式来考察不同断面的驰振性能.研究表明，从横桥向和纵桥向2个方向来看，与直角等边凹进1，0.5 m相比，直角等边凹进0.7 m时的阻力系数接近最小值［7］.因此，本文中倒内凹圆弧、倒外凸圆弧的圆弧半径以及倒直角断面的倒角尺寸均取0.7 m.不同截面形式的工况如表2所示.

图2 双幅桥塔塔柱断面尺寸和间距(单位:m)

表2 双幅桥塔施工期不同断面形式塔柱研究工况

2.3 结果分析

图3为各工况下塔柱的阻力系数和升力系数随风攻角变化的曲线图.图中，CDk和CLk分别表示图2中第k个塔柱的阻力系数和升力系数，k=1，2，3，4.

研究表明，施工期桥塔的纵桥向刚度较大，一般不会发生驰振失稳问题.因此，本文主要研究施工期桥塔在横桥向的驰振性能［6］.单个钝体的阻力系数曲线形状与串列钝体中最上游钝体的阻力系数曲线形状较为接近.由图3可知:①4个塔柱中，塔柱1的阻力系数最大，且随着风攻角的变化，阻力系数在攻角为0°时取得最大值.因此，塔柱间气动干扰效应对塔柱1的阻力系数影响最小.②塔柱3的阻力系数最小，且随着风攻角的变化，所有工况阻力系数曲线变化均较平稳.因此，塔柱间气动干扰效应对塔柱3的阻力系数影响最大.③塔柱2和塔柱4的阻力系数曲线均呈现出较为明显的上凹形状，且塔柱2的阻力系数较小，尤其是在0°攻角附近这种差距更为明显;随着风攻角绝对值的增大，塔柱间气动干扰效应对塔柱2和塔柱4的影响逐渐减小.产生这些现象的主要原因在于:塔柱2距离塔柱3较近，受塔柱3的气动干扰影响，塔柱2的尾流涡旋没有充分展开，尾流较窄;塔柱4除了受到前面塔柱的气动干扰外，后面已没有钝体对其干扰，故尾流产生较明显的涡旋，且相对塔柱2的尾流较宽，故受到的阻力较大;塔柱3离前面钝体最近，受到的气动干扰最大，阻力变化较为平稳，且因前、后塔柱对其干扰，前塔柱与其距离较近，造成分离点位于塔柱3后缘且尾流涡旋不能充分展开，因此其尾流最窄，所受阻力最小.

对于升力系数而言，由图3可知:①随着风攻角的增加，各工况下塔柱1的升力系数均呈下降趋势;②塔柱2的升力系数仅在工况4和7下呈下降趋势，其余工况下均呈波动状态，且下降趋势不明显;③塔柱3的升力系数仅在工况4和10下呈明显的下降趋势，其余工况下均呈递增趋势;④塔柱4的升力系数仅在工况4和10下呈明显的下降趋势，其余工况下均呈波动状态.可见，虽然塔柱1和塔柱3、塔柱2和塔柱4的位置分别相同，但升力系数明显不同，说明上游塔柱的断面类型对气动干扰起决定作用.

图3 各工况下的阻力系数和升力系数

图4为各工况下塔柱的驰振力系数.图中，Gij表示第i种工况下第j个塔柱的驰振力系数.由图可见，工况1和5下的塔柱2和塔柱3以及工况4和10下的塔柱3中均存在驰振力系数小于0的情况.根据登哈托判据可知，仅工况1，4，5，10下的塔柱存在驰振失稳的可能性.工况1下塔柱2的发生攻角约为 － 2°，0°，2°，塔柱 3 的发生攻角约为－8°;工况4下塔柱3的发生攻角约为0°;工况5下塔柱 2 的发生攻角约为 －2°，0°，2°，塔柱 3 的发生攻角约为－8°和8°;工况10下塔柱3的发生攻角在－10°～10°范围内.对比工况1和4可知，矩形断面和倒外凸圆弧断面桥塔较易发生驰振，且距离较近受气动干扰效应影响较大的塔柱2和塔柱3最易出现这种情况.

众所周知，驰振主要发生在类似D形截面的结构中.矩形和倒外凸圆弧断面较倒直角断面和倒内凹圆弧断面更为接近D形截面，故发生驰振可能性更大.气动干扰效应的存在，可能致使群体中某个塔柱发生驰振(见图4(a)和(b)).因此，单纯从驰振稳定性方面考虑，由工况5可知，在倒直角断面桥塔附近再建类似矩形断面的桥塔时，应将其建在倒直角断面桥塔下游;由工况10可知，在倒直角断面桥塔附近再建类似倒外凸圆弧断面的桥塔时，应将其建在倒直角断面桥塔上游.

2.4 单、双幅桥塔驰振性能比较

将图2中塔柱1和塔柱2组成的单幅桥塔作为研究对象，风速方向不变，矩形截面尺寸均取为6.6 m×5.0 m，其中，倒直角断面的倒角尺寸为1 m，倒内凹圆弧断面和倒外凸圆弧断面的倒角尺寸均为0.6 m，特征尺寸B取为6.6 m，分别计算了塔柱间距为1.25B，1.75B和2.25B三种情况下的驰振力系数，结果如图5所示.图中，Gu1，Gu2和Gu3分别表示间距为1.25B，1.75B和2.25B的上游塔柱，Gd1，Gd2和Gd3分别表示间距为 1.25B，1.75B和2.25B的下游塔柱.

图4 各工况下的驰振力系数

由图5可知，对于单幅桥塔，具有矩形断面、倒直角断面和内凹圆弧断面的塔柱2在0°攻角附近存在驰振力系数小于0的情况，且间距越小，驰振力系数越小，即间距越小越易发生驰振失稳.然而，具有倒外凸圆弧断面的塔柱2仅在间距较小时在0°风攻角附近存在驰振力系数小于0的情况，即该类型断面塔柱不易发生驰振失稳.因此，对于单幅桥塔而言，矩形断面、倒直角断面和倒内凹圆弧断面塔柱均存在驰振失稳的可能性，倒外凸圆弧断面塔柱的驰振性能较好.

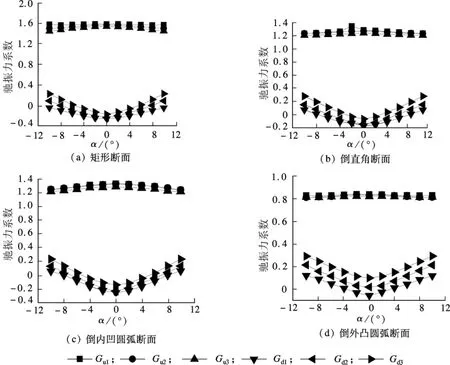
图5 单幅桥塔不同间距塔柱的驰振力系数

对于双幅桥塔而言，由图4可知，由于气动干扰效应，在矩形断面和倒外凸圆弧断面工况下，塔柱2和塔柱3存在驰振失稳可能性，塔柱4则不存在.可见，多塔柱之间的气动干扰可能会使下游塔柱的驰振性能有所改善.

3 结论

1)对于双幅桥塔而言，塔柱间的气动干扰效应对塔柱1的阻力系数影响最小，对塔柱3的阻力系数影响最大.虽然塔柱1和塔柱3、塔柱2和塔柱4的位置分别相同，但升力系数明显不同，说明上游塔柱的断面类型对气动干扰具有重要的影响.矩形断面和倒外凸圆弧断面较易发生驰振，尤其是受气动干扰效应影响较大的塔柱2和塔柱3更易出现这种情况.矩形断面位于倒直角断面桥塔上游时或倒外凸圆弧断面位于倒直角断面下游时，均可能发生驰振.

2)对于单幅桥塔而言，外凸圆弧断面塔柱的驰振性能最好;对于双幅桥塔而言，多塔柱之间的气动干扰可能会使下游塔柱的驰振性能有所改善.

［1］Simiu E，Scanlan R H.Wind effects on structures-fundamentals and application to design［M］.New York:Wiley，1996:230-243.

［2］吕翼，楼文娟，孙珍茂，等.覆冰三分裂导线气动力特性的数值模拟［J］.浙江大学学报:工学版，2010，44(1):174-179.

Lü Yi，Lou Wenjuan，Sun Zhenmao，et al.Numerical simulation of aerodynamic characteristics of three bundled iced transmission Lines［J］.Journal of Zhejiang University:Engineering Science，2010，44(1):174-179.(in Chinese)

［3］ Alonso G，Meseguer J，Pérez-Grande I.Galloping stability of triangular cross-sectional bodies:a systematic approach［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95(9/10/11):928-940.

［4］ Macdonald John H G，Larose Guy L.Two-degree-offreedom inclined cable galloping.Part 1:general formulation and solution for perfectly tuned system［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(3):291-307.

［5］郝浩.桥梁结构的驰振现象及控制［D］.西安:长安大学公路学院，2010.

［6］李胜利.大跨径悬索桥施工期暂态结构抗风性能及控制［D］.哈尔滨:哈尔滨工业大学土木工程学院，2010.

［7］卢桂臣，张红芬.西堠门大桥索塔断面的气动优化［J］.铁道标准设计，2006(1):74-77.

Lu Guichen，Zhang Hongfen.Xihoumen bridge cable tower sections of the aerodynamic optimization［J］.Railway Standard Design，2006(1):74-77.(in Chinese)

［8］陈政清，刘幕广，刘志文.基于气弹模型的串列主缆气动干扰实验研究［J］.振动与冲击，2008，27(8):7-11.

Chen Zhengqing，Liu Mugaung，Liu Zhiwen.Experment study on aerodynamic interference of tandem Cables based on aeroelastic model［J］.Journal of Vibration and Shock，2008，27(8):7-11.(in Chinese)

［9］谭红霞，陈振清.CFD在桥梁断面静力三分力系数计算中的应用［J］.工程力学，2009，26(11):68-72.

Tan Hongxia，Chen Zhengqing.Application of CFD in calculating static coefficients of bridge section［J］.Engineering Mechanics，2009，26(11):68-72.(in Chinese)

［10］刘志文，陈政清，胡建华，等.大跨度双幅桥面桥梁气动干扰效应［J］.长安大学学报:自然科学版，2008，28(6):55-59.

Liu Zhiwen，Chen Zhengqing，Hu Jianhua，et al.Aerodynamic interference effects of twin decks bridges with long span［J］.Journal of Chang’an University:Natural Science Edition，2008，28(6):55-59.(in Chinese)

［11］邓文，葛耀君，曹丰产.桥梁闭口箱梁三分力数值识别中的湍流模型比选［J］.上海公路，2006(4):36-40.

Deng Wen，Ge Yaojun，Cao Fengchan.Silent box girder three component numerical recognition of the turbulence model than the election［J］.Shanghai Highways，2006(4):36-40.(in Chinese)

［12］ Tetsuro Tamura，Tetsuya Miyagi.The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes［J］.Journal of Wind Engineering and Industrial Aerodynamic，1999，83(1/2/3):135-145.

Numerical analysis of aerodynamic interference effect of galloping on bluff bodies in tandem configuration

Li Shengli Lu Yu Wang Dongwei
(School of Civil Engineering，Zhengzhou University，Zhengzhou 450001，China)

In order to investigate the aerodynamic interference effects of galloping on bluff bodies in tandem configuration with different amounts and section shapes，taking the pylon of a long-span suspension bridge as an example，the aerodynamic interference effects of galloping of four columns of twin pylons with four kinds of section shapes were studied by using the numerical analysis method of the computational fluid dynamics(CFD)，which were then compared with those of two columns of a single pylon with the same section shapes.The results show that galloping instabilities can occur when two pylons with rectangular section are in the upstream of those with reverse right angle section or two pylons with reverse outer convex arc section are in the downstream of those with reverse right angle section.For two columns of a single pylon，the galloping instabilities of the downriver column could occur near the wind attack angle of 0°.The closer the two columns are，the bigger the possibility of galloping is.For four columns of twin pylons，the galloping instability for the fourth column of pylon cannot occur because of the aerodynamic interference effect;but for the second and third column of pylon.With rectangular section and reverse outer convex arc section，the galloping instability can occur.

bluff body in tandem configuration;galloping;aerodynamic interference effect;computational fluid dynamics(CFD);numerical simulation

U443.38

A

1001－0505(2012)06-1169-06

10.3969/j.issn.1001 －0505.2012.06.027

2012-06-09.

李胜利(1979—)，男，博士，讲师，lsl2009@126.com.

国家自然科学基金资助项目(50978232，51208471)、中国博士后科学基金资助项目(2011M501190)、高等学校博士学科点专项科研基金资助项目(20114101120008)、河南省教育厅科学技术研究重点资助项目(12A560010).

李胜利，路毓，王东炜.串列钝体驰振气动干扰效应的数值分析［J］.东南大学学报:自然科学版，2012，42(6):1169-1174.［doi:10.3969/j.issn.1001 －0505.2012.06.027］