自适应语音压缩感知方法

罗武骏 陶文凤 左加阔 赵 力

(东南大学水声信号处理教育部重点实验室，南京 210096)

自适应语音压缩感知方法

罗武骏 陶文凤 左加阔 赵 力

(东南大学水声信号处理教育部重点实验室，南京 210096)

针对固定正交基下语音信号稀疏化程度低、适应性差的问题，提出了一种自适应的语音稀疏化方法，并将其应用到语音压缩感知理论中.该方法首先采用线性预测系数的加权线性组合对语音信号进行线性预测，并以线性预测残差基作为信号基.然后，按照稀疏约束条件训练出稀疏表示的过完备字典，并交替应用1-范数稀疏约束的追踪和奇异值分解算法，达到字典与稀疏系数同步更新.该方法从信号特征入手，学习并提取特征或纹理信息，能较好地实现语音信号的稀疏化，提高语音压缩感知的重构性能.实验结果显示，与其他正交基方法相比，该方法的语音稀疏化程度高.语音质量的主客观评价结果显示，该方法具有良好的重构性能.

压缩感知;稀疏性;语音;线性预测

2006年，Candes等［1-2］提出了压缩感知(compressed sensing，CS)理论，在某种程度上突破了奈奎斯特采样定律的限制.压缩感知理论在信息采样上的特性使其具有巨大的吸引力和应用前景，其应用研究已经涉及众多领域［3］，如CS雷达、分布压缩感知理论、无线传感网络、图像采集设备的开发、医学图像处理、生物传感、光谱分析、超谱图像处理及遥感图像处理等.在CS理论中，找到信号的最佳稀疏表示，是应用的基础和前提.

信号的稀疏性研究是信号与信息处理中的一个重要课题.稀疏变换是信号稀疏表示的关键技术，常用的稀疏变换方法有傅里叶变换、小波变换、KL变换以及最近发展的稀疏字典等.傅里叶变换、离散余弦变换(DCT)以及其他一些域［4-5］的变换中都包含固定的正交基，变换比较简单.然而，对于具有复杂结构和特征的信号，例如语音信号(短时平稳，长时间则不具有稳定性)，固定的正交基难以捕获完整信息以使信号在变换域中足够稀疏，因此在稀疏表示方面显现出不足，或者无法很稀疏地表示信号.为了更好地表示变化信号的稀疏性，部分学者提出采用自适应冗余字典的构造方法［6-8］，从信号本身的特征出发，学习并提取特征或者纹理信息.

本文针对固定正交基下语音稀疏化效果差的问题，首先在残差域稀疏的约束条件下对语音信号做线性预测，并求残差，从而得到稀疏变换基;然后，采用自适应训练字典的方法对语音信号进行压缩;最后，采用范数约束算法对语音信号进行重构，并对重构语音进行主客观评价.

1 压缩感知理论

压缩感知的前提条件是信号必须是稀疏的.已知一维离散信号 x={x(1)，x(2)，…，x(N)}T，变换矩阵Ψ=［φ1，φ2，…，φN］的列向量互相正交，其中φi(i=1，2，…，N)为 N×1的向量，则信号 x可以表示为

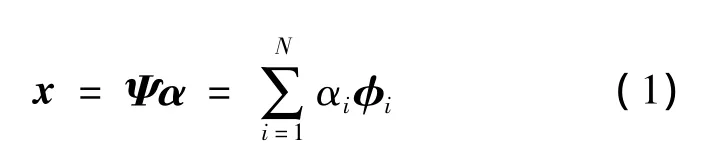
式中，α={α1，α2，…，αN}T为原始信号在变换域中的系数.若对于0＜p＜2且R＞0，α满足，则说明信号x在某种意义下是稀疏的.

如果信号x是L稀疏的，则可以用一个与正交基Ψ不相关的观测矩阵A(A是一个M×N的矩阵，M≪N)对信号x进行线性变换，得到观测向量y(y是一个M维的列向量)，即

将式(1)代入式(2)，得

令AΨ=Θ，则y=Θα.由于y的维数M 远远小于x的维数N，故认为观测信号y已被压缩.

已知y和A求解x，是一个病态问题，即无法直接从测量值y中解出信号x.然而，当式(3)中的α是L稀疏的，即仅有L个非零系数，且L＜M≪N时，根据信号稀疏分解理论中已有的稀疏分解算法，可以通过求解式(3)的逆问题得到系数α，再代入式(1)便可进一步得到信号x.最直接的重构方法是通过l0-范数求解式(3)的最优化问题，即

从而得到稀疏系数α的估计.由于式(4)的求解是个病态问题，而该最优化问题与信号的稀疏分解中求解稀疏的问题十分类似，因此有学者从信号稀疏分解的相关理论中寻找到更有效的求解途径.常用的求解方法有基追踪法(basic pursuit，BP)［9］、匹配追踪法(matching pursuit，MP)［10］和正交匹配追踪法(orthogonal pursuit，OP)等［8］.

2 自适应语音稀疏化方法

2.1 基于线性预测的残差基

传统的线性预测是基于AR模型的，用x中前P个值的加权线性组合来预测x［7］，即

式中，a(k)为预测系数;e(n)为预测误差.通过最小化预测误差e(n)的均方值来估计a(k).考虑到利用预测误差的稀疏性，本文采用1-范数约束预测误差.因此，优化问题可以描述为

令N1=P+1，N2=N，并且假设当n＜1或n＞N时x(n)=0，即相当于对每帧信号加矩形窗.式(6)可根据线性规划进行求解，求出的预测系数a使得预测误差e(n)具有稀疏性质.在预测系数已知的情况下，预测误差可以表示为

式中，B为N×N的矩阵，且由预测系数a构成.因此，式(7)可以改写为

式中，H为B的逆矩阵，也被称之为合成矩阵.矩阵H是将残差域映射到原始时域的基.实际上，H是全极点滤波器的单位脉冲响应矩阵［11］，此处不需要计算B矩阵的逆矩阵，可直接利用H代替.

2.2 自适应的完备字典

基于稀疏表示的过完备字典训练方法(KSVD)［8］能够自适应地按照稀疏约束条件训练出稀疏表示的过完备字典.与传统的完备字典相比，自适应的完备字典具有更强的稀疏表示能力.该方法交替应用1-范数稀疏约束的追踪和奇异值分解算法，实现字典与稀疏系数同步更新.

假设训练信号为矩阵 W=［w1，w2，…，wl］，待训练的字典D=［d1，d2，…，dk］，稀疏系数 Z=［z1，z2，…，zl］，其中 wi表示一帧训练信号.则 K-SVD算法模型可描述为

式中，T0表示稀疏度.

具体的算法步骤如下:

①字典初始化.即将矩阵D赋予初始值，一般情况下，直接将训练信号按照列排列组成比值.

②稀疏编码.当D固定时，式(9)是一个优化问题，即已知W和D求解稀疏系数Z，代价函数可以改写成，因此式(9)等价于

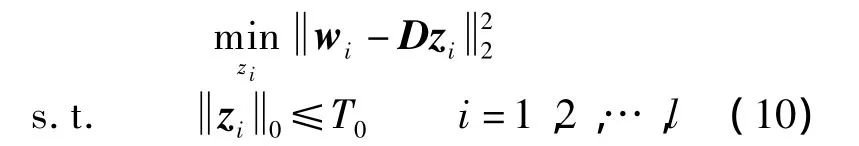
利用基追踪算法即可计算稀疏系数zi.

③字典更新.逐列更新训练字典D，相应的稀疏表示矩阵也同步地逐行更新.记字典D的第K列为dK，在Z中相对应的稀疏表示系数即为第K行的zTK，则式(8)中的代价函数可以改写为

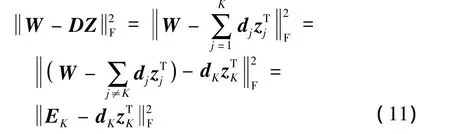
式中表示抽取字典的第K列之后的误差.

在代价函数中，将 DZ抽离成2个部分，即dKzTK以及去掉第K列与第K行相乘的部分.由式(11)可知，EK代表抽取字典中第K列之后的误差.然后，用奇异值分解的方法分解EK来近似表示dK和 zTK.为保证zTK的稀疏性，定义一个矩阵ΩK，其大小为且在位置(wK(i)，i)处的元素值为1，其余位置元素值为0.当矩阵ΩK作用于zTK和W时，会剔除稀疏系数已经为0的信号.

可以利用奇异值分解的方法直接更新字典，本算法中采用字典逐列更新的方式.当所有列都已经更新一遍后，重复步骤②，直至迭代结束［12］.

迭代停止的条件有2种:①限制迭代次数.如在实验过程中得出的经验值是10，则当迭代次数达到10时训练的字典效果已非常明显.②设置一个固定值，当稀疏表示误差达到该值时停止迭代.

3 实验结果与分析

3.1 稀疏性分析

在语音信号稀疏域的分析实验中，安静环境下录制中文男生语音，并对信号进行采样，采样率为8 kHz，每帧包含256个采样点.自适应训练字典在训练时采用同一个人的不同语音语料，时间大约是2 min，即9.6×105个采样点.稀疏度S0的表达式为

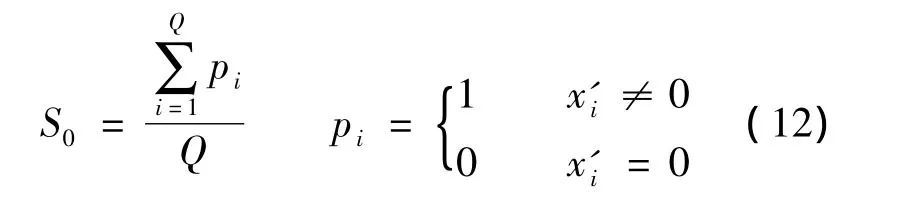
式中，Q为帧长;x'i为稀疏化后的预测系数.

为了说明不同稀疏基对语音信号稀疏表示的影响，比较了语音信号在稀疏基DCT，KL和自适应训练字典基下的平均稀疏度，实验结果见表1.由表可知，DCT变换压缩性能较好，因此具有较好的稀疏性表示.但是，DCT变换缺乏时间/空间分辨率，不能有效地提取具有时频局部化特性的信号的特征.由于DCT变换中基是固定的，因此DCT变换无法自适应地根据当前信号的特点灵活、简洁地表示稀疏信号.KL变换充分运用了当前信号的特征，因而相对于DCT变换在稀疏表示方面表现出了较大的优势.KL变换的缺点是，对每一帧信号都需要重新计算KL变换矩阵，计算量明显增加，影响了压缩感知的实用性.另外，值得注意的是，语音信号分为浊音和清音，浊音具有明显的周期性，清音则类似于白噪声，KL变换对于浊音具有可观的稀疏性，但在清音段却没有稀疏性;语音信号中大部分能量是集中在浊音段的，因此，KL变换对信号恢复的影响不是很大.本文方法与前2种方法最明显的区别在于，前者在稀疏化后绝大部分稀疏值都为0，只有少数几个点有较大值，因而满足绝对稀疏的条件.本文方法最大的优点是信号重构时误差较小，与其他稀疏基相比，训练字典的稀疏性表示效果最好，但付出的代价是训练时间较长.

表1 不同稀疏基下一帧语音的平均稀疏度比较

综上所述，对比各种不同稀疏域的效果，计算复杂度与稀疏性似乎总存在矛盾.采用固定的正交基对信号进行稀疏表示是快速简单的方法，但在稀疏表示方面不够灵活，自适应的残差域和训练的字典能够灵活地捕捉到信号的变化情况，因此能够较好地表示变化的稀疏信号，但同时也导致计算量明显增加.因此，在实际应用中，还需根据具体需求选择稀疏基.例如，实时系统对计算复杂度有严格的要求，合适的固定正交基是首选;后期处理系统对计算精度要求较高，应将自适应的字典作为首选.

3.2 重构性能分析

实验环境是安静的.对2个说话人的语音进行采样，采样频率为8 kHz.每个说话人各录音5 min普通话，而后进行分帧处理(速率为30 ms/帧).稀疏基选取的是线性残差域，重构算法是1-范数约束算法.实验中对男声和女声的语音信号分别进行压缩和重构.为了评估重构算法的性能，采用语音质量评价中常用的客观评价方法和主观评价方法，分别定义如下:

1)主观评价方法.分值算法用于对语音通信系统质量和语音整体满意度进行评价.语音质量的感性评价(PESQ)方法可以根据一些感知标准来客观地评价语音信号的质量，从而提供可以完全量化的语音质量衡量准则［13］.

2)客观评价方法.信噪比(SNR)是一种简单的时域客观评价失真测度.实验中采用帧平均信噪比来衡量重构误差，其定义如下［14］:

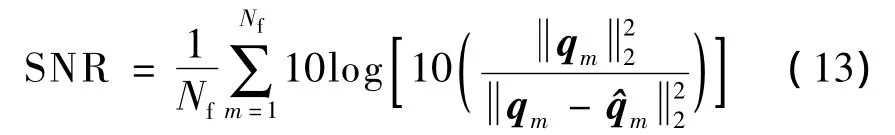
式中，Nf表示总帧数;qm表示语音信号;m表示重构的语音信号.显然，帧平均信噪比越高，重构的效果越好.

表2给出了不同压缩比下男声和女声语音信号的MOS值和信噪比.由表可知，压缩感知的重构性能与压缩比成正比.因此，可以通过适当地提高压缩比来增强语音的重构效果.

表2 不同压缩比下MOS值和信噪比比较

4 结语

压缩感知理论通常涉及观测矩阵选取、稀疏基构造以及重构算法构建3个问题.本文对稀疏基的构建进行了分析和改进，通过实验说明了压缩感知算法在不同稀疏基下对信号稀疏表示的影响.针对固定正交基下语音信号稀疏化程度低、适应性差的问题，提出了一种自适应的语音稀疏化方法，并将其应用到语音压缩感知理论中.该方法从信号特征入手，学习并提取特征或纹理信息，能较好地实现语音信号的稀疏化，提高语音压缩感知的重构性能.实验结果证明该方法具有良好的重构性能.

［1］ Candes E J，Tao T.Near-optimal signal recovery from random projections:universal encoding strategies?［J］.IEEE Transactions on Information Theory，2006，52(12):5406-5425.

［2］ Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［3］石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37(5):1070-1081.

Shi Guangming，Liu Danhua，Gao Dahua，et al.Advances in theory and application of compressed sensing［J］.Acta Electronica Sinica，2009，37(5):1070-1081.

［4］ Davies M E，Daudet L.Sparse audio representations using the MCLT［J］.Signal Processing，2006，86(3):457-470.

［5］梁瑞宇，邹采荣，赵力，等.语音压缩感知及其重构算法［J］.东南大学学报:自然科学版，2011，41(1):1-5.

Liang Ruiyu，Zou Cairong，Zhao Li，et al.Compressed sensing in speech and its reconstruction algorithm［J］.Journal of Southeast University:Natural Science Edition，

2011，41(1):1-5.

［6］ Candes E J，Eldar Y C，Needell D，et al.Compressed sensing with coherent and redundant dictionaries［J］.Applied and Computational Harmonic Analysis，2011，31(1):59-73.

［7］Giacobello D，Christensen M G，Murthi M N，et al.Retrieving sparse patterns using a compressed sensing framework:applications to speech coding based on sparse linear prediction［J］.IEEE Signal Processing Letters，2010，17(1):103-106.

［8］ Aharon M，Elad M A，Bruckstein.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation［J］.IEEE Transactions on Signal Processing，2006，54(11):4311-4322.

［9］ Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit［J］.SIAM Review，2001，43(1):129-159.

［10］Goodwin M M，Vetterli M.Matching pursuit and atomic signal models based on recursive filter banks［J］.IEEE Transactions on Signal Processing，1999，47(7):1890-1902.

［11］ Giacobello D，Christensen M G，Murthi M N，et al.

Sparse linear prediction and its applications to speech processing［J］.IEEE Transactions on Audio，Speech，and Language Processing，2012，20(5):1644-1657.［12］ Elad M，Bruckstein A M.A generalized uncertainty principle and sparse representation in pairs of bases［J］.IEEE Transactions on Information Theory，2002，48(9):2558-2567.

［13］Cristobal E，Flavian C，Guinaliu M.Perceived e-service quality(PeSQ):measurement validation and effects on consumer satisfaction and web site loyalty［J］.Managing Service Quality，2007，17(3):317-340.

［14］ Emiya V，Vincent E N，Harlander，et al.Subjective and objective quality assessment of audio source separation［J］.IEEE Transactions on Audio，Speech，and Language Processing，2011，19(5):2046-2057.

Adaptive compressed sensing method for speech

La Vu Tuan Dao Van Phuong Zuo Jiakuo Zhao Li

(Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education，Southeast University，Nanjing 210096，China)

To overcome the problem that the method of sparsification for speech signal based on fixed orthogonal base has a low sparsity and is not adaptive，a new adaptive sparsification algorithm is developed for speech signal compression.First，speech signal is predicted by linear predication using weighted linear combination of linear predictive coefficients，and the linear prediction residual are used as the signal bases.Then，the adaptive training dictionary is trained under the sparsity constraint，and the dictionary and sparsity coefficients are updated by alternatively using 1-norm sparsity constraint pursuit and singular value decomposition(SVD)algorithm.By analyzing the feature of speech signals，the new scheme can exactly extract essential feature or texture feature，and can obtain better sparsification performance and reconstruction performance for speech signal.The experimental results show that compared with other orthogonal base algorithms，the sparsity of speech signals with the proposed method is obviously improved.The subjective and objective evaluation results of speech quality also show that the proposed method exhibits a good reconstruction performance in speech signal.

compressed sensing;sparsity;speech;linear prediction

TN912

A

1001－0505(2012)06-1027-04

10.3969/j.issn.1001 －0505.2012.06.001

2012-04-05.

罗武骏(1985—)，男，博士生;赵力(联系人)，男，博士，教授，博士生导师，zhaoli@seu.edu.cn.

国家自然科学基金资助项目(51075068，61201326，61231002，61273266)、教育部博士点基金资助项目(20110092130004)、江苏省高校自然科学研究基金资助项目(12KJB510021).

罗武骏，陶文凤，左加阔，等.自适应语音压缩感知方法［J］.东南大学学报:自然科学版，2012，42(6):1027-1030.［doi:10.3969/j.issn.1001 －0505.2012.06.001］