随机极性MCP-EBPSK传输性能

靳 一 吴乐南 冯 熳 邓 蕾

(东南大学信息科学与工程学院，南京 210096)

随机极性MCP-EBPSK传输性能

靳 一 吴乐南 冯 熳 邓 蕾

(东南大学信息科学与工程学院，南京 210096)

为提高随机极性的修正连续相位扩展二元相移键控(MCP-EBPSK)调制信号的传输性能，对比了AWGN信道上自适应门限判决、BP神经网络和支持向量机(SVM)判决3种解调方式的解调性能，并引入了RS码和规则LDPC码来进行改善.根据随机极性MCP-EBPSK调制原理和数字冲击滤波器特殊滤波机理，设计了基于自适应门限判决、BP神经网络和SVM的解调器.同时，在这3种解调方式性能均不佳时，对RS码和规则LDPC编码的随机极性MCP-EBPSK传输性能进行了仿真.仿真结果表明:在AWGN信道上，自适应门限判决、BP神经网络和SVM三种解调方式的解调性能相差不大;当采用自适应门限判决且误码率为10－4时，RS码和规则LDPC码的编码增益分别约为4 dB和7 dB.因此，引入信道编码可显著改善随机极性MCP-EBPSK的传输性能.

修正连续相位扩展二元相移键控;自适应门限判决;BP神经网络;支持向量机;数字冲击滤波器;编码增益

随着信息社会的不断发展，人们对信息传输速率和可靠性的要求越来越高，直接导致空中的无线电频谱资源愈加紧张.如何高效合理地利用有限的频谱资源已成为热门研究课题.从以前的高阶调制到目前的多天线技术(MIMO)［1］、认知无线电技术(CR)［2］均在一定程度上提高了频谱效率，却并未从根本上解决频谱资源不足的问题.超窄带(UNB)调制通过对通信体制的变革从根本上来解决频谱效率的低下问题.文献［3-8］都对此技术进行了深入的研究.然而，超窄带能否真正实用则取决于其传输性能的优劣.

本文对随机极性MCP-EBPSK调制在加性白高斯噪声(AWGN)信道的解调性能进行研究，并分别引入RS码［9］和规则 LDPC 码［10-12］来改善其传输性能.首先，介绍随机极性MCP-EBPSK调制的基本原理.其次，详细阐述数字冲击滤波器［13］的特殊滤波机理，并给出基于幅度差异和波形特征差异的两大类解调器结构.然后，给出信道编码的随机极性MCP-EBPSK通信系统框图.最后，对比和分析基于幅度差异的自适应门限判决和基于波形特征的BP神经网络、支持向量机(SVM)的解调性能，并在AWGN信道分别仿真RS和LDPC编码的随机极性MCP-EBPSK系统性能.

1 随机极性MCP-EBPSK调制

随机极性MCP-EBPSK调制［5］通过在随机极性CP-EBPSK调制中引入一个功率谱形状的调节系数η＜1，来改善功率谱结构，使调制信号的能量更加向载频和功率谱主瓣集中，有利于提升能量利用率，其表达式为

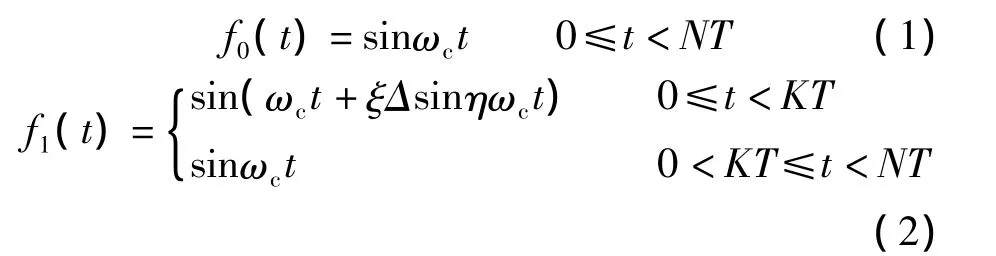
式中，ωc为载波角频率;T=2π/ωc为载波周期;码元“0”持续N个载波周期，码元“1”的相位调制持续K个载波周期，K和N均为整数以保证整周期调制;ξ∈{－1，1}代表了相位调制的极性;0＜Δ＜1为调相指数;η为功率谱形状调节系数，由N，K，Δ和η共同构成了改变信号带宽、传输效率和解调性能的一组“调制指数”.对于“0”码元，发送的调制波形为f0(t)，“1”码元则发送由“ξΔ”共同决定的调制波形f1(t)，由此可在严格的－60 dB带宽下得到很高的频谱利用率.

2 解调器

2.1 冲击滤波原理

数字冲击滤波器［13］是一种具有“陷波-选频”特性的IIR滤波器，在极窄的通带内可将随机极性MCP-EBPSK调制信号的微弱相位变化转化为幅度冲击，且冲击包络不受相位极性影响，增强了调制波形的差异，有利于门限判决和简化接收机结构.在此，选用1对共轭零点和3对共轭极点的数字冲击滤波器，其传输函数为

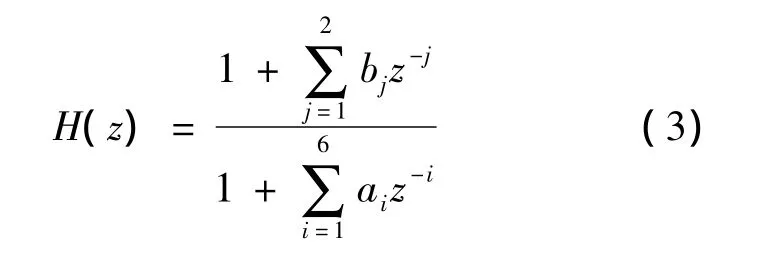
式中

当载频 fc=21.4 MHz，采样频率 fs=214 MHz，N=10，K=2，调相指数 Δ =0.1，η =1/2时，随机极性的MCP-EBPSK调制信号经过上述数字冲击滤波器，得到了如图1所示的冲击波形和输出包络.从图1可看出，数字冲击滤波器的输出包络不受“1”码元的调制相位极性的影响，可在一定程度上放大“0”和“1”调制波形的差异，有利于直接门限判决或采用基于分类器思想的BP神经网络、SVM 解调.

图1 随机极性MCP-EBPSK冲击波形和包络

2.2 2类解调器结构

依据2.1节所述冲击滤波机理，可设计2类不同的解调器:①根据冲击包络幅度的差异，设计基于自适应门限判决的解调器;② 依据冲击包络波形特征的差异，设计基于BP神经网络、SVM等分类器的解调器.2种解调器结构分别如图2和图3所示.其中，图2和图3中的预处理均为取绝对值和低通滤波，即通常的包络检波.

图2 基于自适应门限判决的解调器

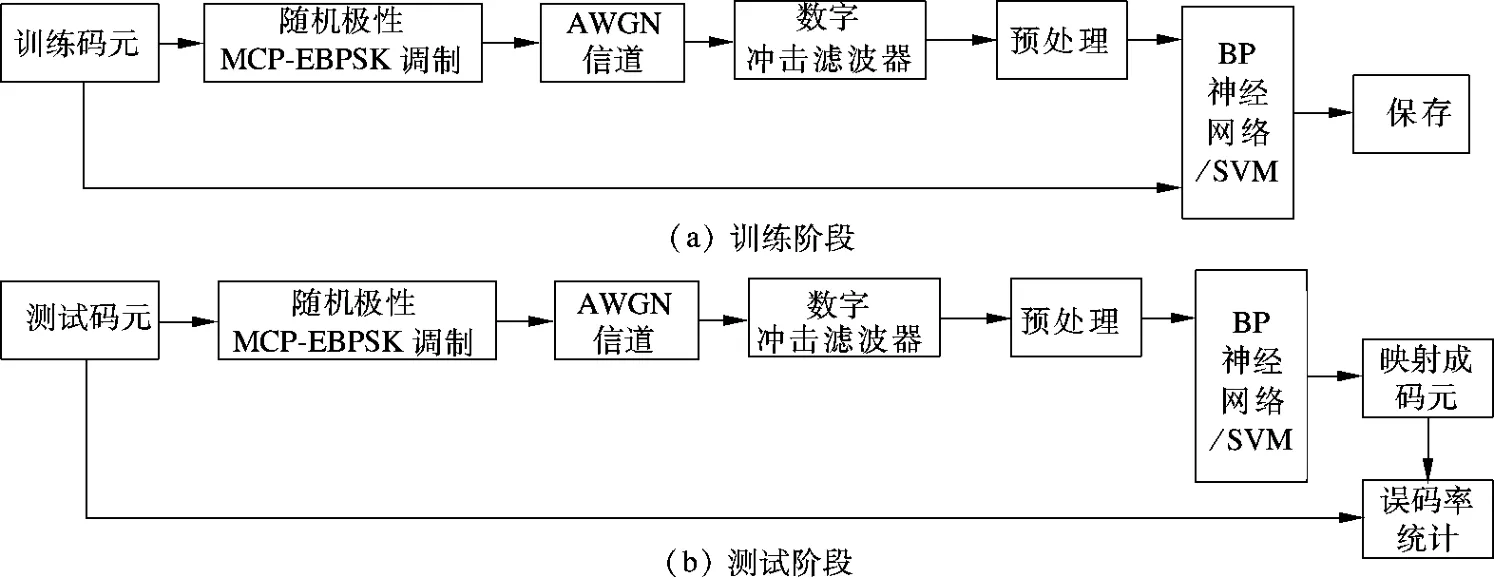
图3 基于BP神经网络/SVM的解调器

3 仿真

图4为信道编码的随机极性MCP-EBPSK通信系统框图.本节首先在AWGN信道对比图2和图3所示2种解调器的解调性能，然后引入RS码和规则LDPC码来改善传输性能.仿真参数均与2.1节保持一致.

图4 随机极性MCP-EBPSK通信系统

3.1 基于BP神经网络的解调性能

在训练信噪比为29 dB，测试信噪比为27～31 dB时，分别在训练样本数为1 000，2 000和3 000的情况下，对基于BP神经网络的解调器进行了仿真，结果如图5(a)所示.同时，在训练样本数为2 000时，分别在训练信噪比为27，29和31 dB的情况下，得到了如图5(b)所示的仿真结果.然后，在训练样本数为2 000和训练信噪比为29 dB时，分别在特征点数为30，40，50和100的情况下进行了仿真，得到了如图5(c)所示的仿真结果.从图5(a)～(c)可以看出，训练样本数和特征点数并非越多越好，当训练样本数为2 000，特征点数为40，而训练信噪比取测试范围的中间值29 dB时，BP神经网络的解调性能较佳.图5(d)给出了该组训练参数下BP神经网络和自适应门限判决的解调性能对比，可看出仅在信噪比超过28 dB时，BP神经网络的解调性能才优于自适应门限判决，且信噪比的最大提升量约为0.5 dB.

3.2 基于SVM的解调性能

在与图5(a)～(c)相同的训练条件下对基于SVM的解调器进行仿真，结果如图6(a)～(c)所示.可看出，与BP神经网络类似，训练样本数和特征点数并非越多越好，当训练样本数为2 000，特征点数为40，而训练信噪比取测试范围的中间值29 dB时，SVM的解调性能较佳.图6(d)给出了该组训练参数下SVM和自适应门限判决的解调性能对比，可看出仅在信噪比超过28.5 dB时，SVM 的解调性能才优于自适应门限判决，且信噪比的最大提升量约为0.5 dB.

3.3 信道编码的随机极性MCP-EBPSK通信系统性能

由3.1节和3.2节可知，以上3种解调方式的解调性能均不佳，这是由于随机极性MCP-EBPSK极小的相位跳变所产生的冲击包络不太明显.本节分别引入不同码长的RS码和规则LDPC码对整个通信系统进行仿真，仿真码元数为1.0×107个，得到了如图7和图8所示的误码率曲线(未采用交织和解交织，因其在AWGN信道中作用有限).图7给出了 RS(15，9)，RS(31，19)，RS(31，23)，RS(63，51)和RS(255，223)等5种不同码长的 RS码和无信道编码时的误码率曲线，可看出，RS(31，19)码性能最好.与非编码系统相比，当误码率为10－4时，RS(31，19)码可获得约4 dB 的编码增益.同时，采用码率为1/2和码长为2 000的规则LDPC码作为信道编码，并借鉴文献［14］中利用SVM的后验概率模型估计EBPSK冲击滤波输出包络的后验概率的思想，利用和积算法译码迭代50次，得到了如图8所示的误码率曲线.可看出，当误码率为10－4时，约有7 dB的编码增益.

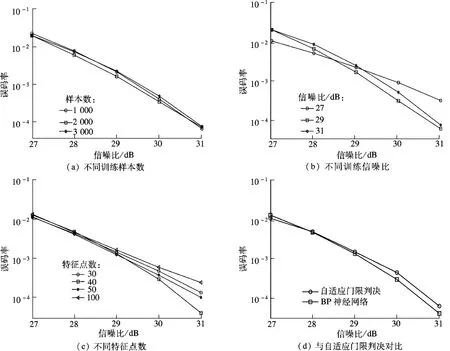
图5 基于BP神经网络的解调器仿真结果

图6 基于SVM的解调器仿真结果

图7 不同码长RS码的解调性能

图8 1/2码率规则LDPC码的解调性能

4 结语

对于AWGN信道，现有的随机极性MCP-EBPSK解调器，无论是基于幅度差异的自适应门限判决，还是基于波形特征的BP神经网络、SVM，其解调性能均不佳.在随机极性MCP-EBPSK通信系统中引入RS码和LDPC码，可获得较大的编码增益.当BER 为10－4时，RS(31，19)码可获得约4 dB的编码增益;码率为1/2、码长为2 000的规则LDPC码可获得约7 dB的编码增益，从而将解调所需的信噪比从超过30 dB降低到25 dB以下，有望用于具有较高信噪比的光纤通信或数字电视信号的电缆传输.

［1］Alamouti S M.A simple transmit diversity technique for wireless communications［J］.IEEE Journal on Selected Areas in Communications，1998，16(8):1451-1458.

［2］ Mitola J，Maguire G Jr.Cognitive radio:making software radios more personal［J］.IEEE Personal Communication Magazine，1999，6(4):13-18.

［3］ Walker H R.Ultra narrow band modulation textbook［M/OL］.(2009)［2011-11-20］.http://www.vmsk.org/.

［4］ Wu Lenan，Feng Man，Qi Chenhao，et al.Recent patents on ultra narrow band modulations［J］.Recent Patents on Signal Processing，2011，1(1):36-47.

［5］靳一，吴乐南，冯熳，等.一种随机极性MCP-EBPSK调制解调器［J］.电子与信息学报，2012，34(7):1647-1652.

Jin Yi，Wu Lenan，Feng Man，et al.An MCP-EBPSK modem with random-polar［J］.Journal of Electronics＆Information Technology，2012，34(7):1647-1652.(in Chinese)

［6］ Zheng Guoxin，Feng Jinzhen，Jia Minghua.Very minimum chirp keying as a novel ultra narrow band communication scheme［C］//The6th International Conference on Information，Communication＆Signal Processing.Singapore，2007:1-3.

［7］ Zheng Guoxin，Yang Weiying.The orthogonal very minimum chirp keying(OVMCK)modulations with very high bandwidth efficiency［C］//Proc of2008IEEE International Symposium of Antennas and Propagation Society.San Diego，USA，2008:3182-3185.

［8］ Li Bin，Zhou Zheng，Zou Weixia.RPPK modulation with high data rates［J］.Science China:Information Sciences，2010，53(2):344-354.

［9］Yar K P，Yoo D S，Stark W.Performance of RS coded M-ary modulation with and without symbol overlapping［J］.IEEE Transactions on Communications，2008，56(3):445-453.

［10］Gallager R G.Low-density parity-check codes［J］.IRE Transactions on Information Theory，1962，8(1):21-28.

［11］Abu-Surra S，Divsalar D，Ryan W E.Enumerators for protograph-based ensembles of LDPC and generalized LDPC codes［J］.IEEE Transactions on Information Theory，2011，57(2):858-886.

［12］ Rybin P，Zyablov V.Asymptotic estimation of error fraction corrected by binary LDPC code［C］//2011IEEE International Symposium on Information Theory Proceedings.St.Petersburg，NJ，USA，2011:351-355.

［13］冯熳，高鹏，吴乐南.超窄带调制信号的特殊滤波分析与仿真［J］.东南大学学报:自然科学版，2010，40(2):227-230.

Feng Man，Gao Peng，Wu Lenan.Analysis and simulation of special filtering based on ultra narrow band modulated signal［J］.Journal of Southeast University:Natural Science Edition，2010，40(2):227-230.(in Chinese)

［14］陈贤卿，吴乐南.EBPSK解调器中利用SVM概率输出的LDPC译码［J］.信号处理，2011，27(9):1286-1290.

Chen Xianqing，Wu Lenan.LDPC decoding via SVM probability output in EBPSK demodulator［J］.Signal Processing，2011，27(9):1286-1290.(in Chinese)

Transmission performance of MCP-EBPSK with random polar

Jin Yi Wu Lenan Feng Man Deng Lei

(School of Information Science and Engineering，Southeast University，Nanjing 210096，China)

In order to improve the transmission performance of random polar and modified extended binary phase shift keying with continuous phase(MCP-EBPSK)modulated signal，the demodulation performance of the adaptive threshold discrimination，BP neural network，and support vector machine(SVM)in additive white Gaussian noise(AWGN)channel is compared，then Reed-Solomon(RS)code and regular low-density parity-check(LDPC)code are introduced.According to the principle of MCP-EBPSK with random polar and the special filtering mechanism of digital impacting filter，the demodulators are designed based on adaptive threshold discrimination，BP neural network，and SVM.Meanwhile，when the demodulation performance of these demodulators is poor，the RS and regular LDPC coded MCP-EBPSK with random polar is also simulated.Simulation results show that in AWGN channel，the demodulation performance of adaptive threshold discrimination，BP neural network and SVM is almost the same;when adaptive threshold discrimination is used and BER is 10－4，the coding gain of RS code and regular LDPC is about 4 dB and 7 dB，respectively.Therefore，channel code can be introduced to significantly improve the transmission performance of MCPEBPSK with random polar.

modified extended binary phase shift keying with continuous phase(MCP-EBPSK);adaptive threshold discrimination;BP neural network;support vector machine;digital impacting filter;coding gain

TN911.25

A

1001－0505(2012)06-1031-05

10.3969/j.issn.1001 －0505.2012.06.002

2012-05-08.

靳一(1984—)，男，博士生;吴乐南(联系人)，男，博士，教授，博士生导师，wuln@seu.edu.cn.

国家自然科学基金资助项目(60872075).

靳一，吴乐南，冯熳，等.随机极性 MCP-EBPSK传输性能［J］.东南大学学报:自然科学版，2012，42(6):1031-1035.［doi:10.3969/j.issn.1001 －0505.2012.06.002］