悬挂建筑结构原型模型的随机振动优化

施明征 涂永明 王志兰

(1东南大学建筑设计研究院，南京 210096)(2东南大学混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

悬挂建筑结构原型模型的随机振动优化

施明征1涂永明2王志兰2

(1东南大学建筑设计研究院，南京 210096)(2东南大学混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

以随机振动为基础，将白噪声作为地面加速度激励，进行悬挂建筑结构原型模型的动力响应优化分析.研究了无约束(即不限制悬挂次结构阻尼比ξ2的上限值)条件下悬挂建筑主结构的最优调谐比fopt、次结构最优阻尼比ξ2，opt、主结构加速度响应方差χa1和主结构位移响应方差χx1等参数与悬挂质量比μ之间的关系，以及在约束(即限制ξ2的上限值)条件下，χa1和fopt与μ之间的关系.结果表明:对具有大悬挂质量比(μ≈1)的悬挂建筑的主结构加速度响应方差进行无约束优化分析时，可以近似假定ξ1=0来求解fopt和ξ2，opt;而对相对位移响应方差优化，采用该假定将带来显著的误差甚至是错误，无约束条件下，χa1随着μ的增大而不断改进.约束优化分析表明，ξ2的上限越大，则χa1和χx1均越小.为了保证悬挂建筑结构的整体动力稳定性，不需要对主结构设置阻尼器，但需要对悬挂次结构(悬挂楼层)设置阻尼器.

悬挂建筑结构;原型模型;随机振动;白噪声

悬挂建筑结构作为一种新型减振结构体系，已日益受到建筑工程界的关注.将悬挂方式应用于房屋结构中，不仅具有强烈的艺术表现力，而且符合结构的自然传力原理，能充分利用高强材料的物理力学性能，以细长的拉杆替代粗大的柱子，扩大建筑使用率，提高结构抗震和抗风性能［1］.

1 悬挂建筑结构的动力计算模型

悬挂建筑结构由主结构、悬挂转换层、悬挂吊杆及悬挂次结构(悬挂楼层)组成［1-2］，如图1所示.其中，悬挂楼层通过转换层结构悬挂于核心筒或者巨型框架等主结构上，这种利用质量巨大的悬挂楼层作为次结构，达到振动控制目的的结构体系，称为悬挂建筑减振体系［3-9］，其主要特点是把整个建筑设计成了一个超级悬挂质量调频阻尼系统［1］，即 SuperSTMD(super suspended tuned mass damper).SuperSTMD的振动控制模型如图2所示.在悬挂建筑结构中，悬挂次结构的各楼层被设计为一个整体，简化为集中质量m2［6-10］，而支撑次结构的主结构(如核筒或者巨型框架柱)以及连接主、次结构的悬挂转换层结构(例如转换大梁)可以简化为集中质量m1，在悬挂次结构与主结构之间应设置减振耗能装置［1，3-9，11-13］.图 2 中，k1及c1表示主结构的刚度及阻尼系数，k2及c2表示悬挂次结构的总抗侧刚度及阻尼系数.

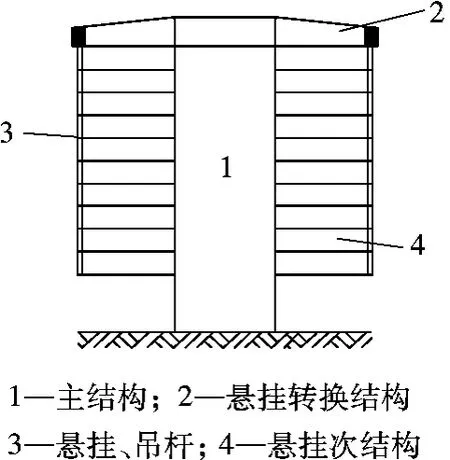
图1 核筒悬挂建筑结构剖面简图

图2 悬挂减振体系控制模型

图2中的悬挂减振体系控制模型在地震动作用下的动力方程为［14］

式中，质量矩阵M、阻尼矩阵C及刚度矩阵K分别为

x为相对于地面的位移向量为悬挂楼段与主体结构的连接刚度，与吊杆两端的约束有关，L为悬挂点与悬挂楼段质心的距离.

设绝对位移为xt，则xt=x+1xg.由此可以得到

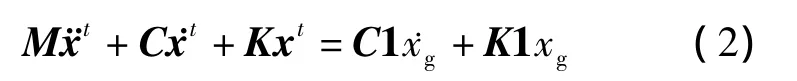
设悬挂建筑结构基础受到谐振动激励，即其中，Ha为绝对加速度频率响应函数向量.由此可以得到

类似地，可以得到悬挂结构的相对位移频率响应函数向量 Hx={Hx1，Hx2}T，其中

2 悬挂建筑结构的随机振动激励响应

地震动作用下的结构响应是随机振动，而地震动加速度谱Sa通常是一个非常复杂的函数，为了便于理论上分析，假定

式中，S0为常数，即白噪声谱.

根据白噪声的定义，可以得到悬挂建筑结构的绝对加速度和相对位移的响应谱，记为

当j=1时，表示主结构的响应;j=2表示悬挂次结构的响应.所以，由式(5)～ (9)，Raj，Rxj可以表示为Ψ/Ω的形式.Ω可改写为

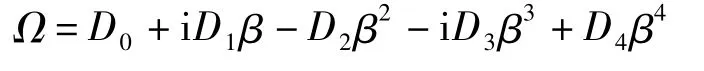
式中，D0=f2，D1=2f(ξ1f+ ξ2)，D2=1+(1+ μ)f2+4fξ1ξ2，D3=2［ξ1+(1+ μ)fξ2］，D4=1;而 Ψ 可统一记为 Ψ =E0+iE1β －E2β2－iE3β3，其中对应的系数列于表1中.

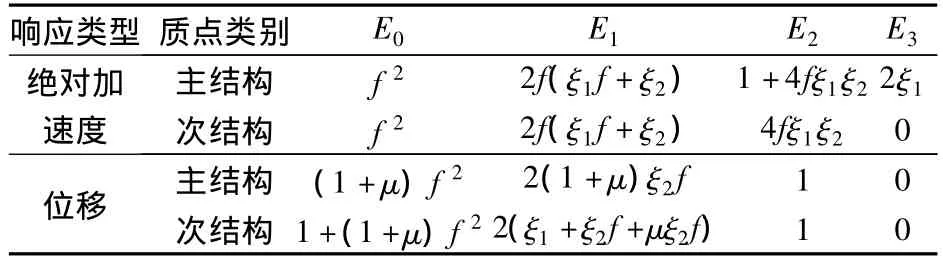
表1 频率响应幅值函数分子系数

因此，式(11)和(12)右侧的积分部分可以记为

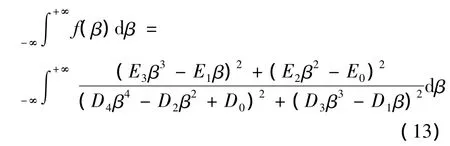
式(13)是一个有理函数的积分，可以采用留数方法计算，即

将表1中的系数和 Ω分别代入式(14)和(15)，可以得到各类情况下的方差响应.式(14)的计算结果如表2所示，其中，下标a1和a2分别对应于悬挂建筑主结构和次结构的加速度响应，x1和x2分别对应于悬挂建筑主结构和次结构的相对位移响应.式(15)的计算结果为

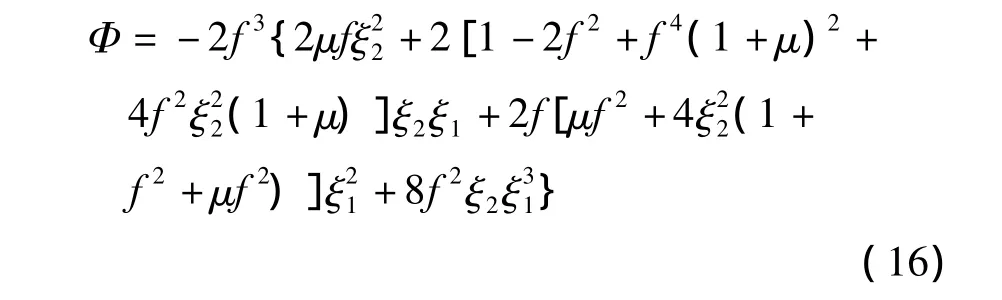
根据表2及式(16)，式(11)和(12)可以改写为

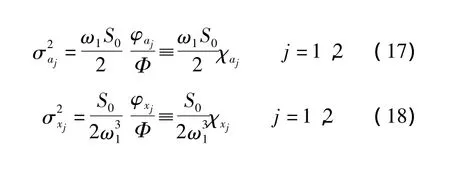
表2 白噪声响应函数的分子表达式

3 悬挂建筑结构随机振动的优化分析

3.1 无约束优化分析

由于对平稳过程的激励分析比较复杂，因此，本文针对悬挂建筑主结构进行分析，以得出相应的优化参数，为保障主结构的安全可靠提供建议.当j=1时式(17)和式(18)即为悬挂建筑主结构的绝对加速度响应和相对位移响应的优化目标函数.

该优化问题是一个无约束的极值问题.取得极值的必要条件是优化函数的驻点存在，即

式中分别表示主结构绝对加速度方差响应(k=1)和相对位移方差响应(k=2).

因为该极值问题是一个实际问题，所以极值点一定存在.分别将表2中的φa1，φx1和式(16)代入式(17)～(19)，可以得到主结构的绝对加速度响应和相对位移响应优化目标函数，即

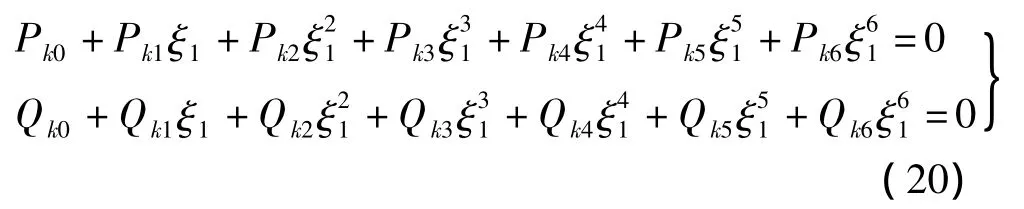
式中，Pkl，Qkl(k=1，2;l=0 ～6)分别为待定系数，k=1时表示加速度响应优化，k=2时表示相对位移响应优化.Pkl，Qkl系数表达式如表3所示.

表3 主结构有阻尼时方差响应优化关系式系数

显然，由式(20)及表3确定的2组代数方程组是高次非线性的，根据代数学的知识，该方程组不能求出解析解.因此，采用数值方法求解式(20).分别取 ξ1=0，0.02，0.05，0.10;令 μ =0.02为初始值，步长为0.02，终止于2.00.由此，绝对加速度方差响应和相对位移方差响应分别得到400个组合，根据每个组合计算出响应最优参数fopt及

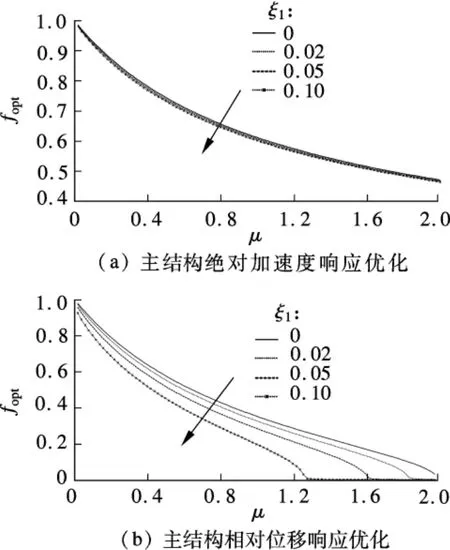
图3 白噪声激励下主结构响应优化fopt-μ曲线

白噪声激励下主结构响应优化的最优调谐比fopt与悬挂质量比μ的关系曲线如图3所示，图中箭头表示ξ1增大方向.可以看到，fopt是μ的单调减函数;μ 一定时，若 ξ1增大，则fopt减小.然而，对于主结构绝对加速度响应优化，ξ1的变化对fopt的影响非常小;对于主结构相对位移响应优化，ξ1的影响则比较显著.这说明，在对主结构加速度响应进行优化分析时，可以采用令ξ1=0的简化方法求解fopt;而对于相对位移响应，采用该简化会在μ较大时带来显著的误差.这些优化参数可以为实际工程提供参考.

类似地，次结构最优阻尼比ξ2，opt与悬挂质量比 μ的关系曲线如图4所示.由图可见，ξ2，opt是 μ的单调增函数;μ 一定时，ξ2，opt为 ξ1的单调增函数.然而，对于绝对加速度响应而言，ξ1对fopt的影响非常小;对相对位移响应，ξ1的影响非常显著.这意味着，采用令 ξ1=0 的简化方法求解 ξ2，opt，对主结构加速度响应优化分析是可行且足够准确的，但对于相对位移响应分析，在μ较大时是错误的.

图4 白噪声激励下主结构响应优化ξ2，opt-μ曲线

上述分析中，主结构阻尼比ξ1=0的计算工况在实际工程中是不存在的，此处选取该工况，是由于传统设置TMD或者STMD的小悬挂质量比(μ≪1)的高层建筑结构动力响应分析方法中采用了主结构阻尼比ξ1=0的基本假定.根据本文计算发现，该传统分析方法(即假定ξ1=0)可以应用于无约束优化下的大悬挂质量比(μ≈1)悬挂建筑结构体系的主结构绝对加速度响应优化，但不能用于主结构的相对位移响应优化.因此传统的小悬挂质量比的结构动力响应分析方法只部分适用于悬挂建筑结构体系.

主结构绝对加速度及相对位移的响应方差χa1－μ 和 χx1－μ 的关系曲线见图 5.可以看到，主结构加速度优化响应随着μ的增大而趋于一个共同的“极限”，而相对位移优化响应在μ＞0.4之后就近似于水平.可见，从理论意义上的优化角度而言，加速度响应的优化值随着μ的增大而不断改进，而相对位移的最优值在μ大于一定数值(例如μ＞0.4)后就趋于稳定.

图5 白噪声激励下主结构响应优化χa1-μ和χx1-μ曲线

在主结构阻尼比ξ1一定的条件下，当悬挂质量比μ大到一定的程度后，其对响应优化效果的影响越来越小.可以认为，μ=1的减振效果已经很好.

3.2 约束优化分析

悬挂建筑结构动力响应的无约束优化可以从数学上得到较为完美的解答，然而，在实际工程中，某些无约束优化最优解无法实现.例如，主结构位移响应的优化参数稳定性很差，当悬挂质量比μ＞1之后，fopt减小并迅速趋于0，如图3(b)所示;而ξ2，opt却迅速增大，很快就不收敛了，如图 4(b)所示.在实际工程中不可能使ξ2，opt无限制增大，或者使fopt趋于0.

由图 4 可见，对于不同数值的 ξ1，ξ2，opt是 μ 的单调增函数，考虑到实际工程中，μ通常较大，例如当 μ =1.0，相应的 ξ2，opt就较大，这在实际工程中很不经济.因此本文中取 ξ2的上限值 ξ2，lim=0.20，以替代最优值 ξ2，opt.

白噪声激励下的结构动力响应约束优化问题可以记为

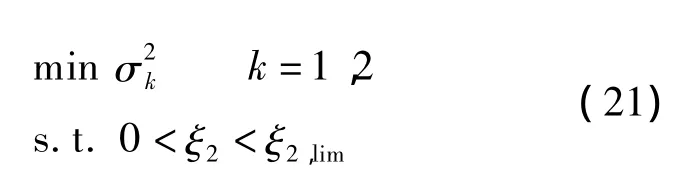
一般地，解决约束优化问题的基本方法主要有惩罚函数法、可行方向法、梯度投影法、既约梯度法、二次逼近法等.因为式(21)的约束条件是线性的，因此可以采用上述各种方法求解;本文采用既约梯度法求解，采用编制计算机程序的方法计算优化参数，取ξ1=0.02和0.05，初始值μ=0.02，步长为 0.02，终止于 2.00;ξ2=0.02，0.05，0.10，0.15，0.20.由此，主结构的绝对加速度响应和相对位移响应如图6和图7所示，图中箭头 表示ξ2增大方向.

图6 ξ2受约束时主结构加速度响应优化fopt-μ及χx1-μ曲线

图7 ξ2受约束时主结构相对位移响应优化fopt-μ及χa1-μ曲线

由图6和图7可知，ξ2的上限越大，则加速度或者相对位移动力响应均越小.而且，fopt是μ的单调减函数;μ 一定时，ξ1增大，fopt减小.ξ1对于主结构相对位移响应优化的影响较大，而对绝对加速度响应影响较小.

图6中，χa1－μ曲线从一条“渐近线”出发，随着μ的增大，而各自分离，不再相交.对于图7中的χx1－μ 曲线，因为次结构无法达到最优阻尼比 ξ2，opt，因而随着ξ2的减小，曲线不收敛.这也说明，从相对位移响应优化的角度，随着μ不断增大，减振效果不提高反降低.相对位移响应不能收敛的性质，在图7的中fopt－μ曲线族中同样表现得非常明显.其原因是最优调谐比fopt太小，而且迅速趋于0(甚至出现负值)，使得刚度矩阵奇异，迭代无法收敛.从图7中还可以发现，ξ1越大，ξ2越小，则动力响应优化越容易导致刚度矩阵退化，从而使迭代计算发散;而这一现象在图6中不容易被发现.因此，对于实际悬挂建筑主结构，通常不需要对主结构设置额外的阻尼器，而需要对悬挂次结构(悬挂楼层结构)设置阻尼器，以保证悬挂结构的整体动力稳定性.

4 结论

1)传统的设置TMD或者STMD系统的小悬挂质量比高层结构动力响应分析方法只部分适用于大悬挂质量比的结构体系.即根据无约束条件对悬挂建筑的主结构加速度响应进行优化分析时，可以采用传统分析方法(假定 ξ1=0)求解fopt和ξ2，opt;而对于相对位移响应，采用该方法求解fopt和ξ2，opt会在μ较大时带来显著的误差甚至是错误.

2)从无约束优化角度而言，悬挂建筑主结构的加速度响应的优化值随着μ的增大而不断改进，而相对位移的最优值在μ大于一定数值(例如μ＞0.4)后就趋于稳定.

3)从约束优化(即限制ξ2的上限值)角度而言，ξ2的上限越大，则悬挂建筑的主结构的加速度或者相对位移响应均越小.在设计建造悬挂建筑时，为了保证悬挂建筑结构的整体动力稳定性，不需要对主结构设置阻尼器，即不需要增大ξ1，而需要对悬挂次结构(悬挂楼层)设置阻尼器，尽量增大 ξ2.

［1］涂永明.CFRP索悬挂建筑结构静力和动力分析及研究［D］.南京:东南大学土木工程学院，2005.

［2］ Dunican P.The art of structural engineering［J］.The Structural Engineer，1966，44(3):97-108.

［3］邓志恒，秦荣.巨型框筒部分悬挂结构控制体系地震反应特性及阻尼控制研究［J］.地震工程与工程振动，2002，22(4):133-138.

Deng Zhiheng，Qin Rong.Study on characteristics of seismic response and damping control for mega-frame tube with partial suspension systems［J］.Earthquake Engineering and Engineering Vibration，2002，22(4):133-138.(in Chinese)

［4］Zhang Y H，Liang Q Z.Asynchronous driving principle and its application to vibration control［J］.Earthquake Engineering and Structural Dynamics，2000，29(2):259-270.

［5］王肇民，邓洪洲，董军.高层巨型框架悬挂结构体系抗震性能研究［J］.建筑结构学报，1999，20(1):23-30.

Wang Zhaomin，Deng Hongzhou，Dong Jun.A study of aseismic properties of huge frame suspended structure in tall buildings［J］.Journal of Building Structures，1999，20(1):23-30.(in Chinese)

［6］涂永明，张继文，吕志涛，等.悬挂建筑减振体系次结构的抗侧性能［J］.东南大学学报:自然科学版，2008，38(6):1099-1104.

Tu Yongming，Zhang Jiwen，Lü Zhitao，et al.Lateral performance of substructure of suspended vibration absorption system［J］.Journal of Southeast University:Natural Science Edition，2008，38(6):1099-1104.(in Chinese)

［7］张伟，张继文，涂永明，等.半刚性悬挂结构体系减振避震机理及参数优化［J］.建筑结构学报，2010，31(12):40-47.

Zhang Wei，Zhang Jiwen，Tu Yongming，et al.Earthquake avoidance mechanism and parameter optimization for semi-rigid suspended structures［J］.Journal of Building Structures，2010，31(12):40-47.(in Chinese)

［8］蔡文华，张继文，涂永明，等.核筒悬挂建筑结构体系的顺风向风致响应分析［J］.工程力学，2011，28(6):103-109.

Cai Wenhua，Zhang Jiwen，Tu Yongming，et al.The analysis of along-wind-induced responses of core-tube suspended building structure［J］.Engineering Mechanics，2011，28(6):103-109.(in Chinese)

［9］张伟，张继文，涂永明，等.基于磁流变阻尼器的半刚性悬挂结构体系避震机理及地震响应分析［J］.工程力学，2012，29(4):141-149.

Zhang Wei，Zhang Jiwen，Tu Yongming，et al.Earthquake avoidance mechanism and seismic response analysis for semi-rigid suspended structure systems using MR dampers［J］.Engineering Mechanics，2012，29(4):141-149.(in Chinese)

［10］Feng M Q，Mita A.Vibration control of tall building using mega subconfiguration［J］.Journal of Engineering Mechanics，1995，121(10):1082-1088.

［11］ Lan Z J，Tian Y J，Fang L，et al.An experimental study on sesmic responses of multifunctional vibrationabsorption reinforced concrete megaframe structures［J］.Earthquake Engineering＆Structural Dynamics，2004，33(1):1-14.

［12］ Lan Z J，Wang X D，Dai H，et al.Multifunctional vibration-absorption RC megaframe structures and their seismic responses［J］.EarthquakeEngineering＆Structural Dynamics，2000，29(8):1239-1248.

［13］ Zhang W S，Xu Y L.Dynamic characteristics and seismic response of adjacent buildings linked by discrete dampers［J］.Earthquake Engineering and Structural Dynamics，1999，28(10):1163-1185.

［14］ Clough R W，Penzien J.Dynamic of structures［M］.3rd ed.Berkeley，CA:Computers and Structures，Inc.，1995:234-242.

Stochastic vibration optimization of prototype model of suspended building structure

Shi Mingzheng1Tu Yongming2Wang Zhilan2

(1Architectural Design and Research Institute，Southeast University，Nanjing 210096，China)
(2Key Laboratory of Concrete and Prestressed Concrete Structure of Ministry of Education，Southeast University，Nanjing 210096，China)

On the basis of stochastic theory，the optimization of dynamic responses of prototype model of suspended building structure was carried out using white noise as ground vibration input.The relationships between four parameters，i.e.the optimal tuning ratio of main structure of building structurefopt，the optimal damping ratio of auxiliary structure ξ2，opt，the acceleration response variance of main structure χa1as well as the displacement response variance of main structure χx1，and the suspended mass ratio μ were analyzed in the case of the unconstrained optimization where the upper limit value of the damping ratio of auxiliary structure ξ2is not limited.Moreover，the relationship between χa1and μ as well as that betweenfoptand μ were analyzed in the case of constraint optimization where the upper limit value of ξ2is limited.The results show that:the damping ratio of main structure can approximately be assumed as zero，i.e.ξ1=0，to solvefoptand ξ2，optin the case of the unconstrained optimization of acceleration response variance of main structure of suspended building with the inherent large suspended mass ratio(μ≈1);however，this assumption could bring large error or even be a mistake in the case of the optimization of displacement response variance.Under the condition of unconstrained optimization，χa1improves with the increase of μ.Moreover，under the condition of constraint optimization，the larger the upper limit value of ξ2is，the smaller the χa1and χx1are.The dampers should not be installed in the main structure but it is needed in the auxiliary structure or in the suspended floors to ensure the global stability of suspended building structure under dynamic excitation.

suspended building structure;prototype model;stochastic vibration;white noise

TU973

A

1001－0505(2012)06-1157-07

10.3969/j.issn.1001 －0505.2012.06.025

2012-05-30.

施明征(1964—)，男，高级工程师，Shimingzheng5182@sina.com.

施明征，涂永明，王志兰.悬挂建筑结构原型模型的随机振动优化［J］.东南大学学报:自然科学版，2012，42(6):1157-1163.［doi:10.3969/j.issn.1001 －0505.2012.06.025］