斜置拉索表面脉动风力特性研究

杜晓庆，顾 明

(1.上海大学 土木工程系，上海 200072;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

斜拉桥拉索的风雨激振(Rain-wind induced vibration)是一种在风雨共同作用下发生的大幅低频振动，峰－峰振幅可达2m，是目前已知拉索振动中振幅最大、危害最严重的一种振动。自1988年Hikami和Shiraishi［1］在日本的MeikoNishi桥上首先发现拉索风雨激振现象以来，国内外许多斜拉桥都有发生拉索风雨激振的报道。

各国研究人员一般采用现场实测［1－3］、风洞试验［4－8］和理论分析［9－13］等方法对拉索风雨激振现象进行研究。通过广泛的研究对风雨激振现象已取得了不少认识，但对拉索风雨激振的发生机理尚未有确切的认识。斜拉桥拉索风雨激振机理研究是近20年来国际风工程和桥梁工程领域的重要研究问题之一。

为了研究拉索风雨激振的机理，研究人员常通过风洞试验，对二维拉索模型(风向角β≠0°，见图2)或三维拉索模型(即倾角α≠0°、风向角β≠0°，见图2)进行了测力或测压试验，以获得斜拉桥拉索的气动性能［6，8－10］。但以往的研究大部分只关注拉索所受到的平均风压分布或平均风力，并在此基础上研究给予准定常假设的拉索风雨激振特性。文献［18－19］通过测压试验研究了二维圆柱体受到的脉动风力特性。文献［21］采用CFD技术对倾角和风向角均为30°的三维圆柱体的表面脉动风压和脉动风力特性进行了分析。迄今为止，还未见到通过表面测压风洞试验研究风向角对三维拉索脉动风力特性影响规律的文献。

另一方面，以往的拉索模型的测力或测压试验研究［6，8－10］仅限于亚临界 Re 数范围内，试验 Re 数在1 ×104～1.5×105之间。随着斜拉桥跨度的增大，拉索直径有增大的趋势，丹麦Oresund High斜拉桥的拉索直径达到250mm［15］，因此拉索发生风雨激振时的Re数很可能会进入临界区(文献［16］中将临界区定义为2.0×105＜Re＜5×105)。Re数进入临界区后，拉索的气动性将发生很大变化，因此有必要研究临界Re数下拉索的气动性能。

针对以上两个问题，本文分别在亚临界Re数和临界Re数下，对三维拉索模型进行了系统的同步测压风洞试验研究。得到三维拉索模型表面的脉动风压分布、风压功率谱、脉动风力及脉动风力功率谱随风向角和Re数的变化规律。本文的研究结果有助于掌握三维拉索的气动性能，有助于进一步澄清拉索风雨激振的发生机理。

1 试验装置及试验工况

1.1 风洞及测试设备

同步测压风洞试验是在同济大学土木工程防灾国家重点实验室TJ－3大气边界层风洞的均匀流风场中进行。该风洞是一座竖向回流式低速风洞，试验段尺寸为15 m宽、2 m高、14 m长。在试验段底板上的转盘直径为3.8 m。试验风速范围从0.2 m/s～17.6 m/s连续可调。流场性能良好，湍流度约为2%、平均气流偏角小于 0.2°。

由美国Scanivalve扫描阀公司的量程为±254 mm和±508 mm水柱的DSM3000电子式压力扫描阀系统、PC机、以及自编的信号采集及数据处理软件组成风压测量、记录及数据处理系统。采样时间为25.6 s;采样点数为8 000;采样频率为312.5 Hz。

1.2 试验模型及参数

为了在拉索模型表面布置足够的测压点，采用放大的拉索节段模型。拉索模型直径为350 mm，模型全长3.5 m，长宽比为10，阻塞率为4.1%。模型直径约为实际拉索直径的2～3倍。为了达到Re数的相似，试验风速设定在5 m/s和10 m/s，分别对应的Re数为1.17 ×105和2.34 ×105。前者 Re数处在亚临界区内，后者Re数则处在临界区内。

拉索模型采用有机玻璃材料，模型通过两端钢支架以固定倾角α=30°支撑在风洞转盘上。为了减小拉索模型的振动，另采用张紧的钢丝作为纤绳扶持钢支架。转盘的转动可调节拉索模型的风向角β。试验装置见图1，拉索模型的倾角和风向角的定义见图2。

为减小拉索模型端部的流体分离对试验结果的影响，模型的上端伸至风洞的顶板;在风向角为0°时，模型下端安装了导流板;当转过一定偏角时，由于模型的下端均处在测点的尾流区内，模型下端的流体分离对试验结果影响不大，因而下端未安装导流板。在拉索模型的四个截面上共布置了176个测压点。

1.3 试验工况

本文作者所做的拉索人工降雨试验表明［7］:拉索在倾角为30°左右，风向角为30°～35°附近时，最易发生风雨激振，且风向角对拉索风雨激振的影响大于倾角的影响。因此在进行测压试验时，将拉索的倾角固定在 30°，试验风向角则分别为 0°、25°、30°、35°、40°和 45°。

2 试验结果及分析

2.1 坐标和测点位置定义

图3定义了拉索模型的坐标系和测点位置的表示方法。图中所示为垂直于拉索模型轴线方向的拉索截面。x坐标轴平行于地面且垂直于拉索模型平面(拉索模型平面为经过拉索轴线且垂直于地面的平面)，以图示方向为正;y坐标轴在拉索模型平面内且垂直于拉索轴线，以图示方向为正。拉索模型上的测点位置用θcyl表示;当风向角β不为0°时，倾角和风向角会引起拉索模型停滞点(拉索模型表面风压系数最大的位置)的变化，停滞点的位置用φ表示。

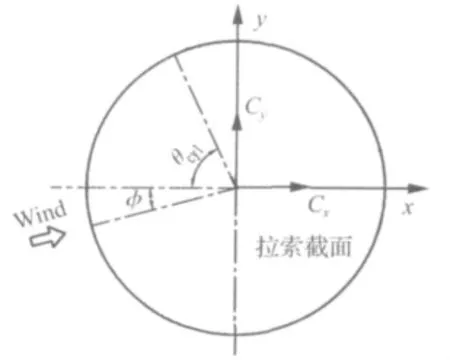
图3 拉索模型坐标和测点位置定义Fig.3 Coordinate system and position of pressure taps

2.2 平均风压

图4为文献［17］中，风向角为0°时拉索模型表面平均风压系数的分布情况。从图4可见:当Re数为2.34×105时，平均风压系数分布呈现临界Re数下的圆柱绕流特征:尾流区变窄，分离点后移至圆柱体背风面，分离点角度在110°左右。Re数为1.17×105时，平均风压系数分布呈现典型的亚临界圆柱绕流特征:分离点在圆柱体迎风面，分离点角度在75°左右。

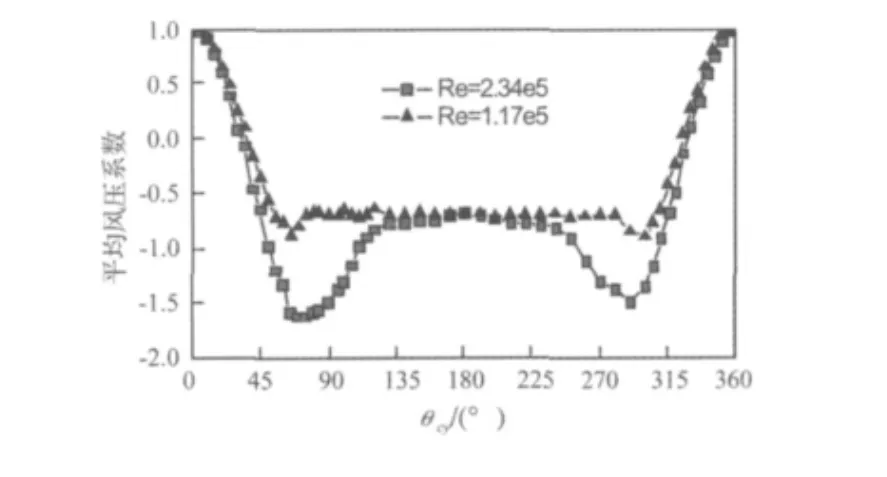
图4 拉索表面的平均风压分布(β=0°)［17］Fig.4 Distribution of mean pressure around cable model(β =0°)［17］

2.3 脉动风压及其功率谱

图5为风向角为0°时，本文两种Re数下拉索表面脉动风压系数分布与文献［18］结果的比较。文献［18］的来流湍流度为 1.4%，Re数为 1.09×105和 2.30×105。

从图5可见，，本文Re数为2.34×105时的脉动风压系数与文献［18］中Re数为2.30×105时的脉动风压系数的分布形态相似。而Re数为1.17×105时，本文脉动风压系数与文献［18］中Re数为1.09×105时的脉动风压系数相比，则差异较大，本文的脉动风压系数偏小。这可能是因为当Re数为1.17×105且湍流度为2%左右时，圆柱绕流已处在亚临界区向临界区的过渡区域中，试验结果对试验模型、试验设备和试验参数等因素的差异非常敏感所导致。

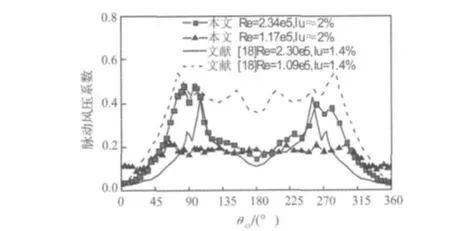
图5 拉索模型表面脉动风压分布(β=0°)Fig.5 Distribution of fluctuating pressure around cable model(β =0°)

当Re数为2.34×105、风向角为0°时，脉动风压系数在圆周表面出现不对称分布，这与Re数已进入临界区有关。脉动风压系数在 θcyl为 80°、100°、260°和 280°附近各有一个峰值，根据文献［18］的分析，80°和260°处的峰值对应层流分离点，100°和260°处的峰值与则边界层再附有关。

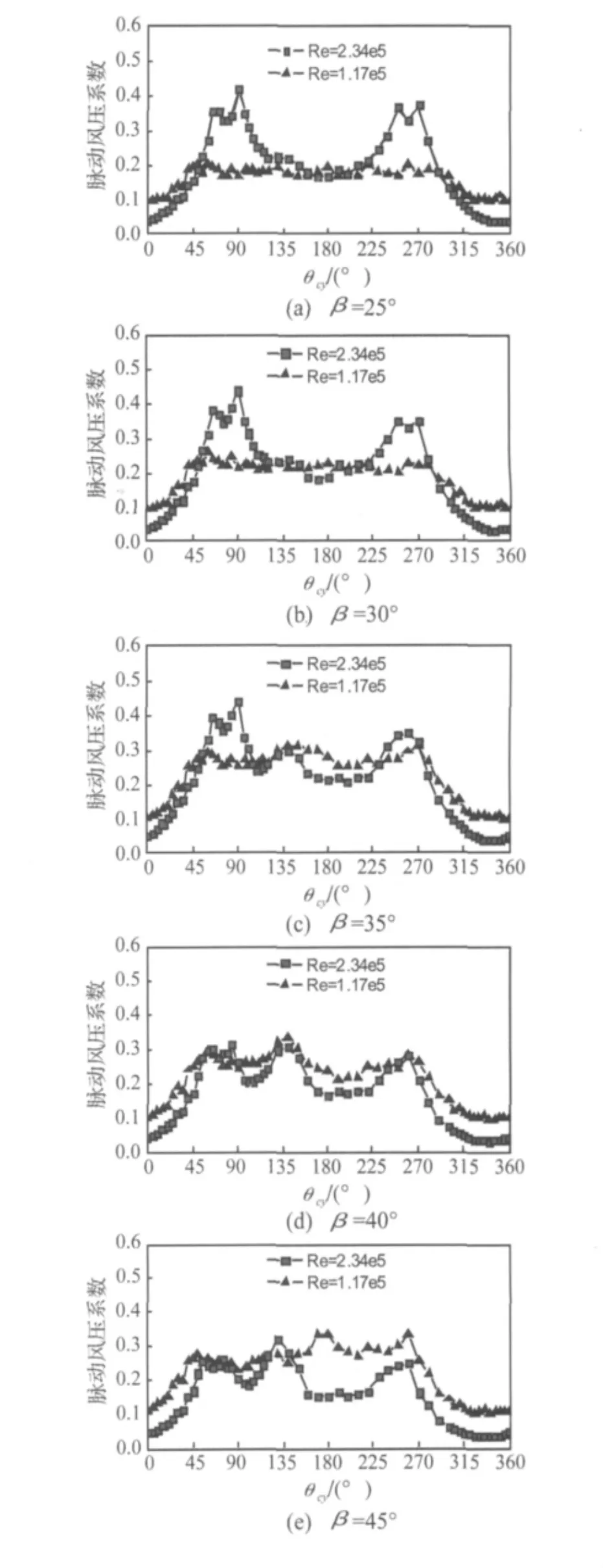
图6 拉索模型表面脉动风压分布 (β=25°～45°)Fig.6 Distribution of fluctuating pressure around cable model(β=25°～45°)

图6为风向角为 25°、30°、35°、40°和 45°时，本文两种Re数下拉索表面脉动风压系数的分布情况。

从图6可见，当 Re数为2.34×105、风向角为25°和30°时，脉动风压系数也有类似的四个峰值。当风向角为35°时，脉动风压系数仅在90°附近出现两个峰值，而在270°附近只有一个峰值。而当风向角为40°和45°时，则在 θcyl为 80°、140°和 260°处各出现一个峰值。这说明当Re数为2.34×105时，风向角的增大会减小边界层再附的可能性。

当Re数为2.34 ×105时，风向角为0°和45°时的最大脉动风压系数分别为0.48和0.32。当Re为1.17×105时，风向角为0°和45°时的最大脉动风压系数分别为0.21和0.33。总体来说，随着风向角的增大，Re数为2.34×105时的脉动风压系数呈逐渐减小的趋势;而Re数为1.17×105时的脉动风压系数则逐渐增大。当风向角为40°和45°时，两种Re数下的脉动风压系数的分布形态较为相似。

图7～图10为两种不同Re数下，风向角为0°和45°时，拉索模型表面典型测点的风压系数功率谱。

由图7可见，当 Re数为1.17×105、风向角为0°时，除了θcyl为0°和180°的测点外，其余测点的功率谱均在Strouhal数(即 St=fU/D=0.17)处有明显的峰值。其中f为卡门涡脱频率，U为来流风速，D为拉索模型的直径。这说明卡门涡脱不但影响拉索模型的背风面，也会影响到拉索模型的迎风面。这一结果与文献［19］的结论基本相同。文献［19］还测得了位于2 St和3 St处的微弱峰值，但由于湍流度的影响(本文湍流度约为2%，文献［19］为0.1%)，本文没有测得这两个峰值。

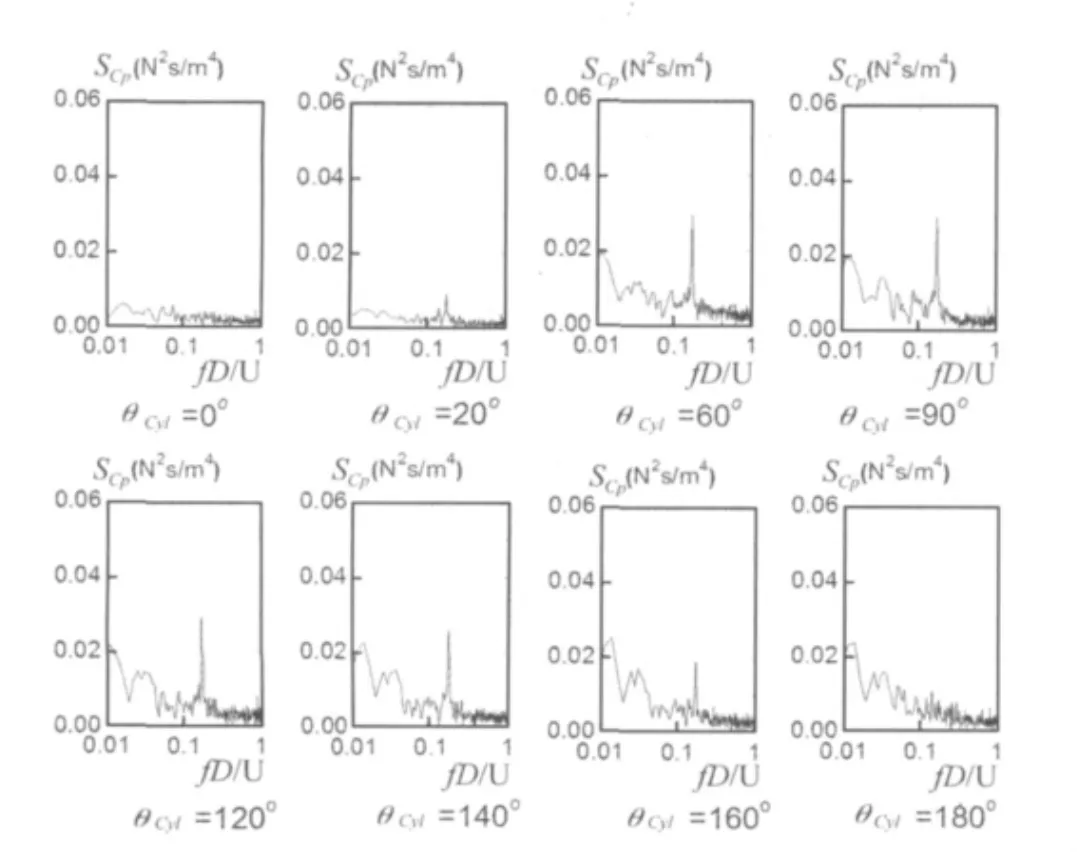
图7 典型测点风压功率谱 (Re=1.17×105，β=0°)Fig.7 PSD of wind pressures on typical taps(Re=1.17 ×105，β =0°)

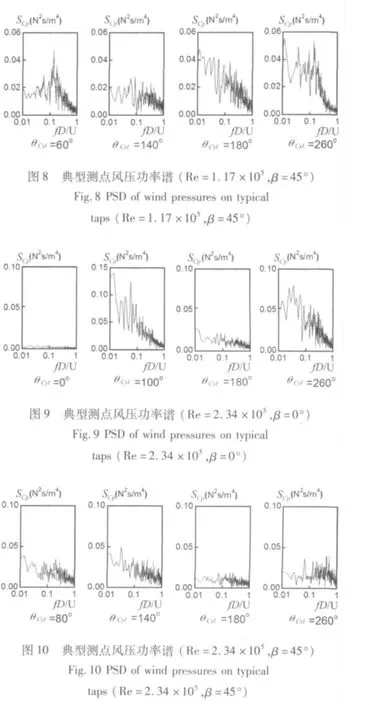
由图8可见，当 Re数为1.17×105、风向角为45°时，θcyl=60°的测点功率谱也有清晰的峰值存在，但此时峰值所对应的 fD/U 为0.14。θcyl为180°和260°的测点(分别对应图6(e)中脉动风压出现峰值的两个测点)功率谱的频率成份比较多，除了在fD/U=0.14附近分布了大量能量外，在低频部分也出现了大量的能量分布。低频部分的能量分布可能与三维拉索背风面的轴向流涡脱有关，下文2.4节将作进一步的分析。

从图9和图10可见，当Re数增大到2.34×105时，各典型测点的功率谱均未出现明显的峰值，但对应图6(a)和图6(e)中脉动风压系数出现峰值的测点位置，风压功率谱往往集中了较多能量。

2.4 脉动风力及其功率谱

设作用在拉索模型上的平均阻力系数和平均升力系数为Cx和Cy，脉动阻力系数和脉动风力系数为Cx’和Cy’，其作用方向见图3。阻力系数和升力系数可通过对拉索模型表面风压系数的积分得到。

图11为两种Re数下，平均风力系数和脉动风力系数随风向角的变化。

从图11(a)可见，随着风向角的增大，两种Re数下拉索的脉动阻力系数基本保持不变。当Re数为1.17×105时，阻力系数的脉动值约为平均值的15%左右;当Re数为2.34×105时，阻力系数的脉动值约为平均值的20%左右。

由图11(b)可见，当Re数为1.17×105时，随着风向角从0°增大到45°，升力系数脉动值从0.10增大至0.23;当风向角为35°时，升力系数的脉动值达到平均值的50%;而当风向角为45°时，升力系数的脉动值甚至超过了平均值。

当Re数为2.34×105时，随着风向角的增大，升力系数脉动值从0.32逐渐减小为0.21;当风向角为35°时，阻力系数的脉动值约为平均值的50%;当风向角为45°时，阻力系数的脉动值约为平均值的35%。

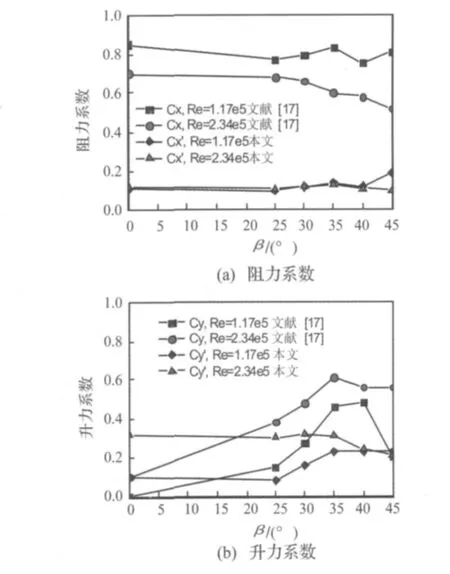
图11 脉动风力系数随风向角的变化Fig.11 Fluctuating wind force coefficients at different wind angles

图12 为 Re=1.17 ×105、风向角为 0°、35°和 45°时，拉索的阻力系数功率谱(SCx)和升力系数功率谱(SCy)。

由图12可见，当风向角为0°时，阻力系数功率谱没有明显峰值，而升力系数功率谱在Strouhal数为0.17处有一突出的峰值。而当风向角为35°和45°时，升力系数功率谱分别在Strouhal数为0.16和0.14处有突出的峰值，阻力系数功率谱在同样的Strouhal数处出现微弱的峰值。这说明随着风向角的增大，Strouhal数有减小的趋势;阻力系数功率谱和升力系数功率谱均会在Strouhal数处出现较为集中的能量分布。

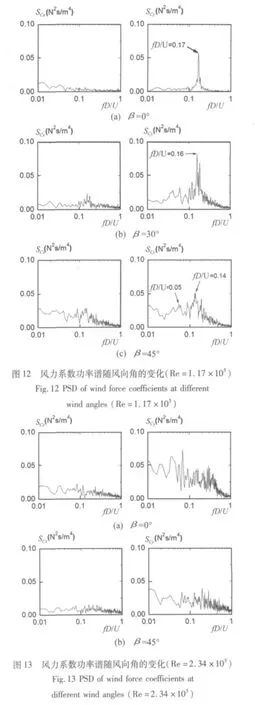
另外，当风向角为45°时，升力系数功率谱在fD/U=0.05(约为Strouhal数的1/3)附近出现较为集中的能量分布，这部分的能量分布可能与轴向流的涡脱有关，在文献［20］中，Matsumoto等通过试验证实:轴向流涡脱频率是卡门涡脱频率的1/3。

图13 为 Re=2.34 ×105、风向角为 0°和 45°时，拉索模型的阻力系数功率谱(SCx)和升力系数功率谱(SCy)。

由图13可见，风向角为0°和45°时，升力系数功率谱均没有突出的峰值存在，这说明当Re数为2.34×105时，在拉索模型尾流区出现较为随机的漩涡脱落，有规律的漩涡脱落被破坏，呈现典型的临界区圆柱绕流特征。

3 结论

本文研究风向角和Re数对三维拉索气动性能的影响，通过对拉索模型脉动风压分布、脉动风力系数及其功率谱等的分析，得到以下结论:

(1)随着风向角的增大，Re数为2.34×105时拉索的脉动风压系数呈逐渐减小的趋势，而Re数为1.17×105时拉索的脉动风压系数则逐渐增大。

(2)当Re数为1.17×105时，拉索的风压系数功率谱和升力系数功率谱均在Strouhal数处有明显的峰值，拉索尾流区存在周期性的旋涡脱落;而当Re数为2.34×105时，则风压功率谱的频率成份较多，没有明显的峰值，拉索模型尾流区出现随机的漩涡脱落，。

(3)当 Re数为1.17×105时，Strouhal数随着风向角的增大而减小。当风向角为0°时Strouhal数为0.17，风向角为45°时的 Strouhal数为0.14。

(4)随着风向角的增大，两种Re数下的脉动阻力系数基本保持不变。当Re数为1.17×105时，脉动升力系数随风向角的增大而增大，当风向角为45°时，脉动升力系数甚至超过了平均升力系数。Re数为2.34×105时的脉动升力系数则随着风向角的增大而减小。

致谢:感谢同济大学防灾减灾国家重点实验室的黄鹏副研究员在本文风洞试验工作中给予的帮助和支持!

［1］ Hikami Y，Shiraishi N.Rain-wind induced vibrations of cables in cable stayed bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1988，29:409－418.

［2］ Persoon A J，Noorlander K.Full-scale measurements on the Erasmus Bridge after rain/wind induced cable vibrations［A］.Wind Engineering into the 21stCentury［C］.Balkema，Rotterdam，1999，1019－1026.

［3］ Main J A，Jones N P.Full-scale measurements of stay cable vibration［A］.Wind Engineering into the 21stCentury［C］.Balkema，Rotterdam，1999，963－970.

［4］ Flamand O.Rain-wind induced vibration of cables［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，57:353－362.

［5］ Matsumoto M，Saitoh T，Kitazawa M，et al.Response characteristics of rain-wind induced vibration of stay-cable of cable-stayed bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，57:323－333.

［6］ Cosentino N，Flamand O，Ceccoli C.Rain wind induced vibration of inclined stay cables，part 1:experimental investigation and physical explanation ［J］.Wind and Structures，2003，6:471－484.

［7］ Gu M，Du X Q.Experimental investigation of rain-windinduced vibration of cables in cable-stayed bridges and its mitigation［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005，93:79－95.

［8］ Xu Y L，Li Y L，Shum K M，et al.Aerodynamic Coefficients of Inclined Cylinders with Artificial Rivulet in Smooth flow ［J］.Advances in Structural Engineering，2006，9(2):265－278.

［9］ Yamaguchi H.Analytical study on growth mechanism of rain vibration of cable［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990，33:73－80.

［10］ Gu M，Lu Q.Theoretical analysis of wind-rain induced vibration of cables of cable-stayed bridges［J］.Journal of Wind Engineering，2001，89:125－128.

［11］ Wilde K，Witkowski W.Simple model of rain-wind-induced vibrations of stayed cables［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91:873－891.

［12］ Xu Y L.Wang L Y.Analytical study of wind-rain-induced cable vibration:SDOF model［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91:27－40.

［13］ Cosentino N，Flamand O，Ceccoli C.Rain wind induced vibration of inclined stay cables，part 2:mechanical modeling and parameter characterization ［J］.Wind and Structures，2003，6:485－498.

［14］ Gu M，Du X Q，Li S Y.Experimental and theoretical simulations on wind rain-induced vibration of 3－ D rigid stay cables［J］.Journal of Sound and Vibration，2009，320:184－200.

［15］ Larose G L，Smitt L W.Rain/Wind Induced Vibrations of Parallel Stay Cables［A］.IABSE Conference［C］.Sweden，1999:301－310.

［16］ Simiu E，Scanlan R H.Wind effects on structures［M］.John Wiley ＆ Sons，Inc.1996.

［17］ 杜晓庆，顾 明.临界雷诺数下斜拉桥拉索的平均风压和风力特性［J］.空气动力学学报，2010，12(6):639－644.

［18］ Norberg C，Sunden B.Turbulence and reynolds number effects on the flow and fluid forces on a single cylinder in cross flow ［J］.Journal of Fluids and Structures，1987，1:337－357.

［19］ Nishimura H， TaniikeY. Aerodynamiccharacteristicsof fluctuating forces on a circular cylinder［J］.Wind Engineering into the 21stCentury［C］，Journal of Wind Engineering and Industrial Aerodynamics，2001，89:713－723.

［20］ Matsumoto M，Yagi T，Shigemura Y，et al.Vortex-induced cable vibration of cable-stayed bridges at high reduced wind velocity［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89:633－647.

［21］ 李寿英，顾 明.斜、直圆柱绕流的CFD模型［J］.空气动力学学报，2005，23(2):222－227.