基于局部线性嵌入和云神经网络的转子故障诊断方法

孙 斌，薛广鑫，陈 军，蒋能飞

(东北电力大学 能源与动力工程学院，吉林 132012)

从大量的振动数据中找出有效的特征信息是汽轮机运行状态在线监测和故障诊断的一个重要环节，故障特征提取关系诊断结果的准确程度。传统的转子状态监测和故障诊断方法主要是基于傅里叶变换和小波变换理论，傅里叶变换能够计算出信号时域或频域特征参数的统计结果，却无法同时兼顾时域和频域的全貌和局部化特征。小波变换在傅里叶变换的基础上增加了可调窗口的功能，被称为“数学显微镜”，然而小波基函数的长度有限，在变换过程中会产生能量泄露，小波基函数和分解尺度限制了分析频率的范围，缺乏自适应性[1－2]。

局部线性嵌入(Local Linear Embedding，LLE)是流形学习的一种，它的基本思想是发现隐藏在高维数据中不能直接观察的结构信息，获得一个能够保持高维数据特征的低维嵌入[3－5]。LLE算法只考虑一个全局最优解，在权值优化时只需对局部计算，在计算上简单可行;在求解低维嵌入时把问题转化为求解一个稀疏矩阵的最小特征值问题，使得LLE算法在运算效率上优于其他流形学习方法[6－8]。

本文采用了“原始信号－构造特征矩阵－数据降维(特征提取)－模式识别”的故障诊断模式，其中“数据降维”采用了局部线性嵌入方法，使用云神经网络完成模式识别。为了获得理想的低维嵌入，本文构造一个由振动信号组成的矩阵作为LLE算法的输入矩阵。与相空间的构造方法不同，是在原始信号中分段截取等长数据段并把它们组合成一个矩阵作为特征矩阵，最后用云神经网络对LLE算法得到的低维矩阵的分类效果进行测试[9－10]。对正常和故障转子振动信号的分析说明该方法能有效地用于转子系统故障诊断。

1 局部线性嵌入算法

LLE算法是一种非线性降维算法，它的基本思想是保将高维空间数据投影到低维空间中而不改变原有流形在局部的相互关系。LLE算法包括三个步骤:确定每个点样本点的邻域，计算重构权值矩阵W，利用矩阵W计算低维嵌入，具体算法如下。

1.1 寻找每个样本点的K个近邻点

设矩阵 X=(x1，x2，…，xN)，xi是 D 维列向量，根据度量空间距离:

计算任意两个样本点之间的欧式距离(p=2)，得出样本点xi的K个距离中最近的点作为xi的K近邻。

1.2 计算重构权值矩阵

定义一个误差函数:

其中:xij(j=1，2，…，K)是 xi的 K 个近邻点，wij表示 xi和xij之间的权值，且满足条件:

将式(3)代入式(2)得:

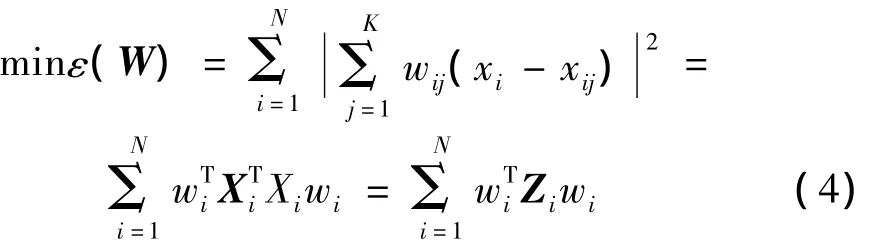
1.3 将所有样本点映射嵌入到低维空间

映射满足条件:

其中:φ(Y)是输出函数，yi是 xi的输出向量，yij(j=1，2，…，k)是yi的k个近邻点，且满足两个条件:和可以存储在N×N的稀疏矩阵 W 中。当 xj是 xi的近邻点时，Wi，j=wij，否则，Wi，j=0。用Wi表示W 矩阵的第i列，Ii表示N ×N 单位矩阵的第 i列，Y 表示输出向量，即 Y=(y1，y2，…，yN)，则式(5)可写为:

要使损失函数值最小，则Y取M的d个最小非零特征值所对应的特征向量，将M的特征值按从小到大排列，一般地，第一个特征值几乎等于零，因此取从2～d+1共d个特征值所对应的特征向量作为输出结果Y。

2 云神经网络

2.1 云的基本概念

设U是一个用精确语言描述的定量论域U={x}，T是与U相联系的语言值。U中的元素x对于T所表示的定性概念的隶属度Cr(x)是一个具有稳定倾向的随机数，Cr(x)∶U→[0，1]，∀x∈U，x→Cr(x)。隶属度在论域上的分布称为隶属云，简称云。云用期望值Ex、熵En、超熵He三个数值来表征。

2.2 云发生器及其改进

给定云的3个数字特征(Ex，En，He)，产生正态云模型的若干云滴 drop(xi，μi)(i=1，2，…，n)，称为正向云发生器。其中:xi为定性概念的具体量化值;μi为xi属于定性概念的隶属度。

已知云模型(Ex，En，He)，有条件x=x0的云发生器称为X条件云发生器，有条件μ=CT(x)=CT(x0)的云发生器称为Y条件云发生器，如图1所示。相应的算法如下[11]:

图1 云发生器Fig.1 Cloud generator

2.3 云神经网络

云模型广泛应用于数据挖掘等领域[12]，但结合神经网络的云理论在工程实践中还应用非常少。其中田永青[13]在简化的T－S云模型控制器基础上提出了一种云神经网络结构，并应用于某地税收预测。该网络是根据简化云模型推导出的多输入单输出模型，工程应用不便。为此，本文采用文献[14]提出的云神经网络模型，结构如图2所示。该网络中，有m个输入，n个输出，5层分别是输入层、云化层、隐含层、逆云化层和输出层。在云化层使用X正态云发生器，在逆云化层使用Y正态云发生器，在隐含层使用连续可导的传递函数。

在学习过程中，使用误差反向传播算法。设云神经网络的输入为X，输出为Y，仿真输出为Ys，隐含层节点为k个，隐含层传递函数为f。

图2 云神经网络结构Fig.2 Structure of the cloud neural network

当输入为xi(i=1，2，…，m)，则云化层输出为:

隐含层输出为:

“不用慌，他怀疑你谋杀是没有根据的，有动机，但没有证据，你怕什么？再说现在受益人不是咱们，很难说他更怀疑谁，他只是在试探你们，别理他。”

逆云化层输出为:

云神经网路的性能函数为:

3 故障诊断实验

3.1 实验数据采集

转子振动实验台(如图3)模拟振动信号，人为制造一些故障来模拟汽轮机转子的振动。实验装置包括:转子振动实验台、ZXP－4A型数字测振仪主机、电涡流传感器、DASP信号采集器以及计算机等。模拟的故障分为3类，包括:转子质量不平衡、不对中以及松动和不对中耦合。各种故障模拟的方法为:不平衡故障通过在临近电涡流传感器的转子转盘上旋入3～5个螺钉，螺钉要集中以使转子发生不平衡故障;不对中故障是将联轴器换成硬质橡胶管，并在轴末端的轴承座底垫上1～2个垫片，人为将轴承座扭转一定角度实现;松动和不对中故障耦合则是在一次实验中加入轴承座松动和转子不对中两种故障实现。

图3 转子振动实验台Fig.3 Experiment of rotor vibration

故障信号的原始采样频率为1 000 Hz，采样点数为8 000点，实验中，转子转速分为1 000 r/min，1 150 r/min和1 200 r/min三种。每个转速下一种故障采样10组数据。

3.2 特征矩阵构造

在使用LLE算法之前需要构造一个能够代表振动信号的矩阵。在时间序列分析中，相空间重构的理论能够利用时间序列的特性构造一个由时间序列组成的矩阵，但是用相空间重构方法构造的矩阵作为样本输入LLE算法进行测试的结果表明，分类效果不明显。本文在相空间重构理念的基础上提出一个新的特征矩阵构造方法。

本文所用信号由不平衡、不对中以及不对中加松动三类故障信号组成，分析频率为1 000 Hz。

如图4所示，分别截取了三类故障信号的100个点画出一个原始信号波形示意图。观察波形图可知，不对中信号相对于其他两种信号比较平滑，出现的局部峰值点比较少;不平衡信号振动比较强烈，局部峰值点比较多。从整体来上，三类信号都表现出了一定的周期性特征，在长度为100个采样点的范围内每个信号大约有3.5个近似周期;观察振动信号的局部波形特征，发现有一些特有的波形会重复出现，而且各类振动信号的局部特有波形不同。如果能将局部波形差异放大，即可获得该信号区别于其他信号的特征矩阵。

图4 原始振动信号Fig.4 Original vibration signals

考虑到LLE算法的第一步是求出高维数据的K个近邻点，也就是说在构造的特征矩阵的各个样本点之间搜索距离最近的点，为了体现出某一类信号的特征必须保证计算出的近邻点之间距离在某一个特定的范围内，那么每一个样本点信号都能够用同一类的信号表示。设时间序列为S(s1，s2，…，sn)，算法步骤如下:

(1)求出S中所有极值点。如果si的模大于si－1，si－2并且大于 si+1，si+2，那么 si就是所要找的极值点。

(2)确定基点。对所有的极值取绝对值，然后求出其算术平均值，如果极值si大于平均值，那么si就是所要找的基点。

(3)获得样本点。以基点为起始点截取一定长度的数据作为一个样本点。取值长度的大小会影响LLE算法近邻点的选取，本文选取长度为3～4个近似周期的数据。

(4)将所有的样本点逐列排列组成一个矩阵，即所要的特征矩阵。

3.3 故障诊断流程

基于局部线性嵌入和云神经网络的故障流程如图5所示。

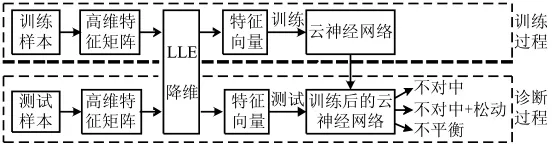
图5 故障诊断流程图Fig.5 Process of fault diagnosis

具体诊断步骤如下:

(1)采集转子的故障信号，并分为训练样本和测试样本两部分。

(2)按照3.2中的方法构造高维特征矩阵，并运用LLE算法进行降维，降维后的低维特征向量作为云神经网络的输入。

(3)以不对中、不对中加松动、不平衡3种模式作为网络的输出，确定网络结构，对网络进行训练。

(4)用训练后的云神经网络对测试样本进行测试。

4 结果与分析

利用上述方法构造一个特征矩阵X，用LLE算法对矩阵X降维后得到了一个低维的矩阵Y，当输出矩阵Y的维数是2或3的时候，可以用图形显示分类效果。当维数高于3维时需要利用分类器来识别，本文采用云神经网络。

4.1 低维流形

如图6所示，按照数据长度为80个点，分别在转子不对中、不对中加松动和不平衡三种故障信号随机抽取44个样本点构造了一个132×80的特征矩阵;当K=5，d=3时用LLE算法对该特征矩阵降维得到了低维空间表示。从三维图可以看出每一类数据都能比较集中的分布一个特定区域，3类数据在空间分布上有明显的区别;二维图比较清晰地反映了三类数据在空间上的区分程度，不对中信号在V2方向上对应于－1，在V1方向上沿着一条直线较为集中分布在－1、－0.5和1三个点的附近;不对中加松动信号沿斜线方向分布在0和－1两个点的附近分布比较集中，不平衡信号在V1方向分布在1的附近，在V2方向上均匀分布。

4.2 云神经网络诊断结果分析

图6 低维流形图Fig.6 Lower manifold figure

上述N，m，K，d四个参数对低维流形都有较大的影响，因此需要进行多次试验验证该方法的可行性，并选取一组比较合适的参数以获得更好的诊断效果。从三维流形和二维流形图可以看出，3类数据并没有完全分离，而是在某一个区域内分布比较集中，各类数据在空间分布上有明显的差异。实际上各类数据在低维流形上存在一定的交叉区域，试验表明LLE算法的参数K取值过大时，各类数据在低维流形上的投影趋于一个区域，分类效果不明显;当K取值过小时受到LLE算法本身的局限性所得结果不够精确，因此需要通过实验选择一个最优值。其中N和m取值与矩阵构造有关，对低维流形有一定的影响。

图7 故障诊断率与近邻点数K的关系Fig.7 The relationship between fault diagnosis rate and nearest neighborhood K

图7 为当 N=60，m=44，d=3，云神经网络(隐层节点数为15)的诊断率随近邻点数K变化的曲线，每类故障的诊断率都是经过5次实验取平均值得到的统计结果。从图中可以看出，在近邻点为3－9的范围内时诊断率较高，平均在83.3%以上，在K=7时总体诊断率达到最大值。随着近邻点数的取值增大，诊断率呈现波动整体诊断率下降，当K＞10时，不对中加松动故障的诊断率明显的下降，而其他两种类型的故障诊断率基本上在70%以上，分析其可能原因有:

(1)不对中与不对中加松动两种故障的振动信号都有不对中的故障成分，增加了两种故障的区分难度;

(2)近邻点K取值过大导致诊断率下降，因为LLE算法要求找出一个样本点的K个最近邻样本点并用这些样本线性表示，K值过大使得线性表示出现误差。

图8为当 N=60，m=44，K=9，云神经网络(隐层节点数为15)的诊断率随LLE算法嵌入维数d的变化关系曲线，可以看出当d取3、4时诊断率较高，随着d的增大诊断率呈下降趋势。不对中与不对中加松动两种故障的诊断率随d的变化趋势一致，3种故障的诊断率下降是由于输出在低维空间投影很接近而导致的。实验发现，构造特征矩阵的数据段长度N和个数m对诊断率也有一定的影响，但影响程度较小。

图8 故障诊断率与嵌入维数d的关系Fig.8 The relationship between fault diagnosis rate and embedding dimensionality d

当近邻点数K=9，嵌入维数d=4时，3类故障各取13个样本测试得到的诊断结果见表1。此外，为了验证云神经网络的分类效果，本文还设计了一个三层BP神经网络和一个RBF神经网络，神经网络的训练样本和测试样本均与云神经网络相同。BP网络的隐层节点数为12，训练最大步数选择为2 000，误差指标为0.001，诊断率见表1。从表中可以看出，每种故障的13个测试样本中，云神经网络的错分样本数分别为2个、1个和1个，总体诊断率达到了89.74%，而BP网络的错分样本数分别为3个、2个和2个，总体诊断率为79.49，RBF网络的总体诊断率为87.18%，可以看出在训练样本相同的情况下，云神经网络的诊断率高于BP网络和RBF网络，表现出更好的分类性能，从而验证了本文提出的特征提取方法及诊断方法的可行性。

表1 故障诊断结果Tab.1 The results of fault diagnosis

5 结论

本文研究了流形学习方法在转子故障诊断中的应用，并提出了一种利用局部线性嵌入(LLE)算法和云神经网络的转子故障诊断方法。LLE算法需构造一个高维特征矩阵，本文提出了基于峰值对齐的构造方法。实验验证了该方法构造的矩阵可将时间序列的处理与流形学习联系在一起，能准确诊断转子的振动故障。同时分析了算法中几个参数对诊断结果的影响，发现近邻点数K和嵌入维数d对诊断结果影响较大。与BP神经网络和RBF神经网络相比，云神经网络具有更高的诊断率。

致谢:本文受到了东北电力大学研究生创新基金(2010)资助。特此感谢。

[1]于德介，陈淼峰，程军圣，等.基于EMD的奇异值熵在转子系统故障诊断中的应用[J].振动与冲击，2006，25(2):24－26.

[2]彭文季，罗兴锜.基于小波包分析和支持向量机的水电机组振动故障诊断研究[J].中国电机工程学报，2006，26(24):164－168.

[3]Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290(5500):2323－2326.

[4]Tenenbaum J B，Silvavd，Langford J C.A global geometric framework fornonlineardimensionality reduction[J].Science，2000，290(5500):2319 －2323.

[5]徐 辉.基于流形学习的特征提取[D].西安:西安电子科技大学，2010.

[6]Ridder D de，Duin R P W.Locally linear embedding for classification[R].Delft，Netherlands:Pattern Recognition Group，Dept of Image Science ＆ Technology，Delft University of Technology，2002.

[7]李伟生，张 勤.基于局部线性嵌入和Haar小波的人脸识别方法[J].计算机工程与应用，2011，47(4):181 －187.

[8]马 瑞，王家廞，宋亦旭.基于局部线性嵌入(LLE)非线性降维的多流形学习[J].清华大学学报(自然科学版)，2008，48(4):583 －586.

[9]Samuel K，Martin D L.Face detection in gray scale images using locally embeddings[J].Computer Vision and Image Understanding，2007，105(1):1 －20.

[10]Cox T F，Cox M A A.Multidimensional scaling(2nded.)[M].Chapman and Hall，2001.

[11]刘常昱，冯 芒，戴晓军，等.基于云X信息的逆向云新算法[J].系统仿真学报，2004，16(11):2417－2420.

[12]杨薛明，苑津莎，王剑锋，等.基于云理论的配电网空间负荷预测方法研究[J].中国电机工程学报，2006，26(6):30－36.

[13]田永青.基于云模型的数据挖掘算法的研究与应用[D].上海:上海交通大学，2003.

[14]徐宗本，樊忠泽.基于云神经网络的空间推进系统故障检测与诊断[J].兵工学报，2009，30(6):727 －732.