基于双渐进方法的水下爆炸气泡载荷作用下舰船的动态响应分析

张 弩，宗 智，张文鹏，孙 雷，李章锐

(大连理工大学 工业装备结构分析国家重点实验室 船舶工程学院，大连 116024)

舰船在水下爆炸载荷作用下的动态响应是一个非常复杂的问题，需要涉及水下爆炸载荷的模拟，爆炸气泡的动力学特性，流固耦合分析及水中结构的非线性动态响应等多项研究内容。目前，对于这类三维结构动态问题的主要研究方法是边界元/有限元结合的方法。主要采用流固耦合方程来表征耦合界面上的载荷，而不需要对水域进行建模，因此减少了大量的计算量。这种方法主要经历了平面波理论[1]，曲面波理论[2]，虚质量理论[3]到双渐近(DAA)理论[4－6]的发展过程。特别是由Geers所提出的DAA理论，综合并改进了前面几种方法，在高、中、低频段都有较好的精度。DAA方法经过众多学者们的改进与发展[7－10]，目前是一种解决流固耦合问题的非常有效的计算方法。

水下爆炸中对舰船主要产生两种载荷:一是瞬态的冲击波，其压力峰值很高但持续时间很短，通常造成水中结构的局部破坏;二是气泡脉动载荷，气泡中大约含有47%的爆炸能量，具有非常强的破坏力。这一阶段的明显特征是达到的压力峰值较冲击波的压力峰值低，而且持续时间很长，约为几百毫秒，会造成水中结构的总体响应和局部响应[11－12]。

对于气泡的动力学，众多学者已经进行了大量的研究工作[13－19]。对于气泡载荷作用下的舰船的动态响应，目前的主要研究方法都是将舰船简化为船体梁，研究船体梁的总体鞭状响应[20－26]。然而，对于气泡作用下三维全船结构的动态响应的细节分析，开展的研究还很少。

本文致力于建立一套有限元方法与DAA方法相结合的计算程序，用以研究水下爆炸气泡作用下水面舰船的动态响应。首先，建立一个考虑迁移效应，自由面效应和气泡阻力的气泡模型和一个水面舰船结构模型，并阐述了流固耦合与结构响应相关的理论分析;然后以该船模作为算例，研究了气泡作用下船体模型的总体响应和局部响应。比较了不同位置的加速度，速度和位移时程曲线。最后详细讨论了气泡作用下船体模型动态响应的特征与机理。

1 理论背景

1.1 控制方程

一个弹性结构受到外部激励的运动方程可以表示为:

其中:Ms，Cs，Ks分别为N×N阶的质量矩阵，阻尼矩阵和刚度矩阵。N×1阶向量分别为结构的位移，速度和加速度。列向量F代表外力。N为结构的自由度总数量。

对于浸没在流体的结构所受的外部激励可以表示为:

式中:pi和ps分别为湿表面上入射流和辐射流作用下产生的节点压力向量，Af为湿表面单元的面积对角矩阵，G为结构节点力和湿表面节点力的坐标转换矩阵。

当一个水中结构如水面舰船或潜艇浸没在无限声学流体介质中，结构湿表面的壳单元的控制方程可以由DAA方法来表示。对于流体中的弹性结构，DAA方法表示的结构表面流体的运动即为各正交流体边界模态的线性组合。一阶双渐近DAA方程的矩阵形式表达为:

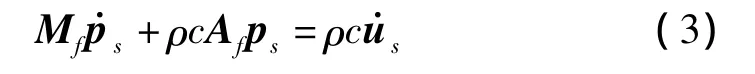
式中:Mf为N×N阶的流体质量矩阵;ρ和c分别为流体密度和流体中声速;us是辐射流的流体法向速度向量。

根据在流固耦合湿表面上，结构和流体的法向速度相等的条件，得到:

式中:ui为入射流的流体法向速度向量。

将式(2)代入式(1)，式(4)代入式(3)，得到了下面的流固耦合方程组:

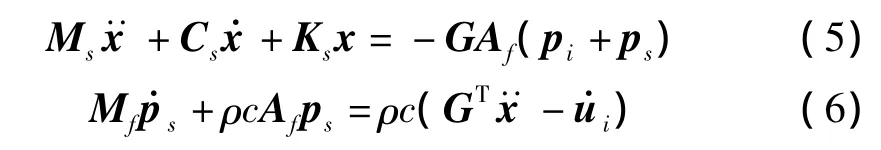
将式(8)左右两边同乘以GAfM－1f，得到:

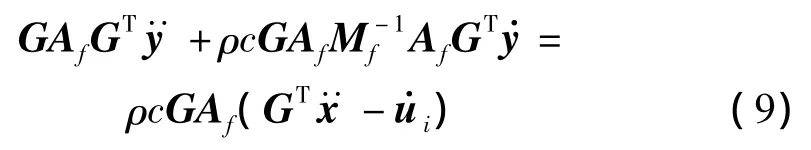
这样式(7)和式(9)就可以联立进行数值耦合求解。

1.2 气泡载荷

冲击波之后，大约47%的爆炸能量仍然存留在气泡中。假设流体为无旋，不可压缩的，气泡中心在自由水面下深度d处。由于本文考虑的是中远场爆炸，假设船体对气泡没有影响，并且气泡在运动过程中保持球形。为考虑气泡的迁移效应，自由面效应和气泡阻力的影响，采用Vernon[27]的无量纲方程组:

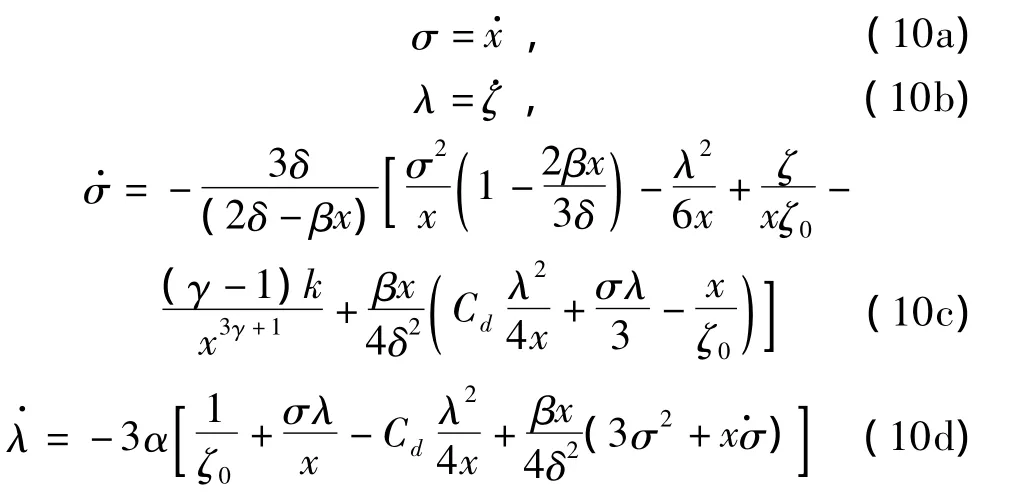
式中:x是无量纲气泡半径，ζ0为无量纲初始压头。ζ为无量纲压头，τ为无量纲时间;δ为无量纲深度，k是无量纲能量参数(对于 TNT炸药，k≈0.074 3(z0)1/4，z0为初始压头)，γ 为绝热气体参数，取为 1.25[11]，Cd为阻尼系数，取为2.5。α为气泡迁移控制系数(α只取值0或1;α=0表示不考虑气泡的迁移效应)。在本文中取α=1。β为自由面效应控制系数，同样只取值为0或1;β=0表示不考虑自由面效应。在本文中取β=1(即考虑自由面效应)。

接着定义L为长度尺度因子，T为时间尺度因子。

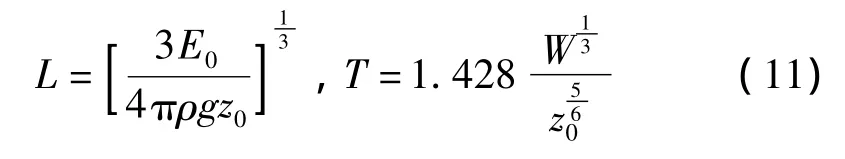
式中:E0为爆炸的总能量，ρ为流体的密度，g为重力加速度，W为炸药量。可以得到以下无量纲参数:

其中:z为压力水头。

只要给定初始条件，式(10a)～(10d)可以由四阶龙格库塔法进行求解。选定初始条件为x=x0，ζ=ζ0，σ=0，λ =0。而其中 x0可以由下面能量守恒方程[25]得到:

方程(10a)～(10d)的解即为x(t)和ζ(t)。速度势函数可以表示为:

式中:r为所取源点到气泡中心的径向距离，r1为该源点对应的偶极到气泡中心的径向距离。θ为r方向与垂直方向的夹角，θ1为r1方向与垂直方向的夹角。e1为源强系数，e2为偶极强度系数，定义如下:

对于势流，速度为速度势的负梯度，即为:

式中:X和Y分别为以气泡中心作为原点的直角坐标系的横坐标和纵坐标。

流体加速度可以表示为:

其中:ν为气泡的垂向平均速度。

式(20)中的两项可以分别表达为下面两式:

2 求解方法

本文的程序中，首先利用有限元方法提取结构质量矩阵和刚度矩阵，然后利用一阶DAA方法来求解流体方程。一阶DAA方法实质上是在高频频域段和低频频域段分别采用平面波近似理论和虚质量近似理论进行逼近近似，中频段采用线性的过度。这样就可以在从高频频域到低频频域的区域都具有较高精度。文献[6]通过对浸没在水中的圆形球壳的数值计算结果与精确解的比较，验证了一阶DAA方法在求解一般问题上的精度可以满足要求。而程序中的三维流体质量矩阵利用边界积分方法进行求解[28]。在进行耦合计算时，采用分部交错迭代(Staggered solution)的方法，在每一个时间步内，采用预报－代入－判断－同步的方式进行迭代。结构的计算采用Wilson－θ法，考虑到计算的稳定性，流体的计算采用隐式的单步求解方法。计算程序流体图如图1所示。

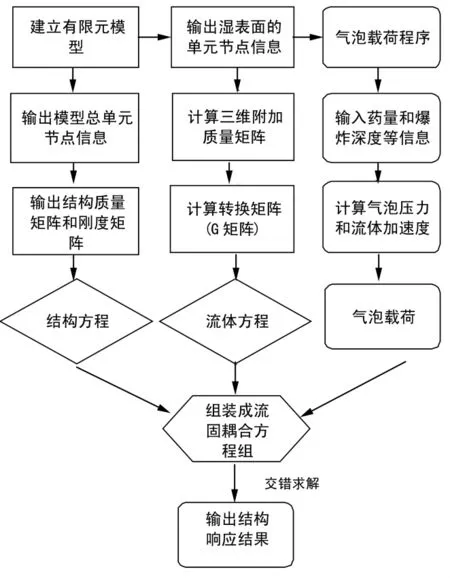
图1 计算程序流程图Fig.1 Flow chart of the calculation procedure

3 算例分析

取一艘船模作为算例来分析其在气泡载荷作用下的动态响应。示意图如图2所示。此船模总长4.5 m，型宽0.6 m，型深0.45 m，吃水T=0.265 m，排水量390 kg。船模共设7道横舱壁、两层平台，有中纵舱壁，平台2与船底外底板组成双层底。甲板、平台1、平台2的板厚4 mm，其余结构的板厚3 mm。采用普通钢建造，密度 ρ=7 850 kg/m3，弹性模量 E=210 GPa，泊松比 μ=0.3，屈服极限约为235 MPa。

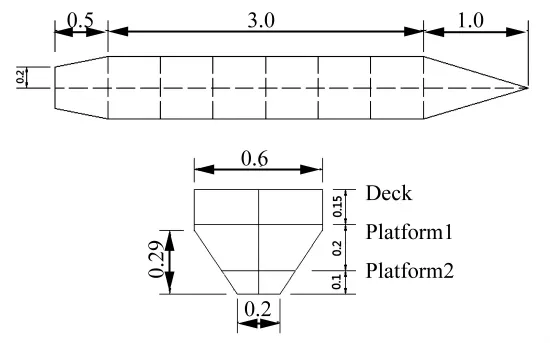
图2 船模的结构示意图Fig.2 Schematic diagram of the ship model

船模的有限元模型如图3所示。船模共有2 373个节点，2 648个单元，其中包括661个湿表面单元。对于非接触水下爆炸，破坏力最大的情况是炸药在舰船正下方发生爆炸。所以本文中，假设药包在船中正下方爆炸，如图3所示，爆炸的位置可以由爆炸深度h来表示。

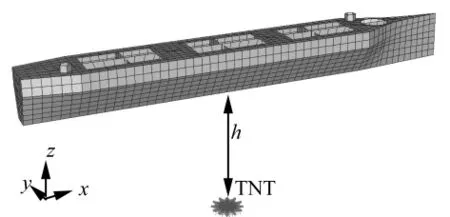
图3 船模的有限元模型Fig.3 Finite element model of the ship-model

取6 kg TNT炸药在自由表面下10 m处爆炸。为忽略冲击波效应的影响，取爆炸后0.05 s作为初始时间。气泡半径，气泡压力和气泡中心深度的时间历程曲线如图4所示。从图中可以看到，气泡半径先增大到最大值，然后在t=0.26 s时减小到最小半径。在这个过程中，随着气泡半径的减小，气气泡压力随着气泡半径的减小而增加。当气泡半径减小到最小值之后，气泡开始回弹，因为此时气泡内部压力已经变得非常大。随后气泡半径随着时间而增大。在回弹过程中，气泡压力迅速衰减到零以下。当气泡半径在最大值附近时，气泡中心位置上升的很缓慢，而当气泡半径要达到最小值时，气泡开始快速地向上迁移。

图4 气泡半径，深度和压力的时间历程曲线Fig.4 Time histories of bubble radius，depth and pressure

图5 给出了一系列不同时刻的船模的垂线位移响应。其中云图给出的是全船的响应分布情况，云图下方的曲线表示船底龙骨的位移响应。从图5中可以清楚地观察到船模在气泡在作用下的位移响应主要为船体的总体响应。船模按梁的一阶垂线振型进行总体鞭状运动。这主要因为气泡载荷的频率较低，与船体的低阶垂向固有频率相接近，因此激起了船体的低阶振型，使船体发生鞭状运动。船中处位移最大，图中可以看到最大位移可达到2.4 cm。这样的鞭状振动使船中反复遭受作用力，严重时会对船体造成较大的总体损伤。

为进一步研究船模在不同位置处的响应特性，在船模的中线面上取几个典型的位置作为测点。其中包括船底龙骨上的测点(B1，B2，B3)和主甲板上的测点(D1，D2，D3)。测点的具体位置如6所示。

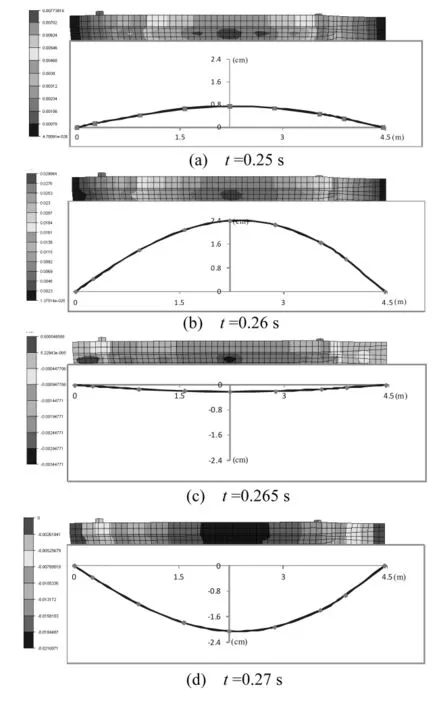
图5 不同时刻船模的垂向位移响应Fig.5 Vertical displacement responses of the ship model at different times

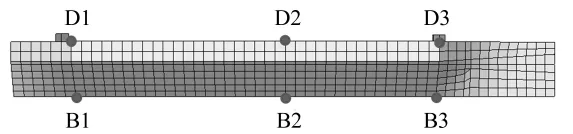
图6 不同测点的分布位置Fig.6 The locations of different test points

图7 给出了不同测点的加速度，速度和位移响应的时程曲线。从图中可以观察到所有测点的加速度，速度和位移响应均开始于大约0.25 s时，这是气泡载荷开始迅速增长至峰值的时刻。然后响应的幅值开始缓慢平滑的衰减。由于炸药位于船中的正下方，所以船中的测点B2和D2的加速度，速度和位移的峰值要比其他测点大很多。如B2的最大加速度值为1 869.6 m/s2，分别约为 B1(726.8 m/s2)和 B3(1 474.8.8 m/s2)的2.57倍和1.27倍。速度和位移响应也遵循同样的规律。在同一纵向位置，主甲板和船底龙骨处的响应相差不大。如B1和D1，B2和D2，B3和D3的加速度，速度和位移的峰值都比较接近。

图7 船模不同测点的加速度、速度和位移响应Fig.7 Acceleration，velocity and displacement responses of the ship model at different test points

除了船体的总体响应，船模上的一些区域也出现了明显的局部响应，如图8和图9所示。图8给出了在t=0.260 s时刻的垂向位移响应。可以观察到在船中处的舷侧外板上有明显的局部大位移响应区域。在此区域取两个测点T1和T2，如图所示，此时T1的垂向位移为3.19 cm，T2的垂向位移为2.73 cm。两者相差17%。结合图5(a)～(c)中的位移云图，可以看到沿着船长方向，在舷侧外板上还有几个位置均出现了局部大位移响应区域，分布在船中两侧，比船中处小一些。

图8 船模的局部垂向位移响应Fig.8 Local vertical displacement response of the ship model

图9 给出的是t=0.271 s时刻船模的垂向加速度响应。可以观察到在主甲板的舱口处，出现了明显的局部加速度集中区域。同样取测点T3和T4，如图所示，此时T3的垂向加速度为3 166.12 m/s2，T2的垂向加速度为1 520.66 m/s2。T3为T4的2.08倍。这是因为船舶甲板舱口角隅，由于形状不连续，在船体发生鞭状运动受到较大的面内载荷时，使局部的应力梯度升高，产生应力集中，严重时可能会造成塑性变形与屈服。因此在结构设计时，为了降低这种应力集中程度，应该采取加厚板、复板或形状优化设计等使舱口角隅的最大加速度极小化。

图9 船模的局部垂向加速度响应Fig.9 Local vertical acceleration response of the ship model

通常认为，水下爆炸主要引起船体的垂直方向的响应。其实在某些位置，船体的横向响应也较为明显。图10给出的是t=0.258 s时刻船模的横向位移响应。可以观察到沿着船长方向，在舷侧外板上有多处较大的局部大位移区域，尤其在艏尖舱壁位置尤为明显，在艏尖舱壁处出现了面积非常大的局部大位移响应区域，而且左右两侧的位移是相反方向的。在左右两侧分别取两个对称的测点T5和T6，它们的加速度时间历程曲线如图11所示。可见两个测点一直在做相位相反的振动，即按壳体的呼吸模态振动。而两个测点T5和T6的横向加速度峰值分别为 2 899.9 m/s2和2 784.7 m/s2。它们已经和上面分析的垂向加速度在同一量级，严重时会造成船体结构的局部破坏，必须引起重视。

图10 船模的局部横向位移响应Fig.10 Local transverse displacement response of the ship model

图11 测点T5和T6处的横向加速度响应比较Fig.11 Comparison of transverse direction accelerations at T5 and T6

4 结论

本文通过建立一套有限元方法与DAA方法相结合的计算程序，研究了水下爆炸气泡作用下水面舰船的动态响应。主要结论为:

(1)水下爆炸气泡脉动载荷作用下，船体结构的响应主要以总体响应为主。船体发生了显著的鞭状运动。且主要表现为低阶模态响应，即一阶弹性振型。

(2)气泡作用下，在船体的某些位置，局部垂向响应也非常显著。如船中处的舷侧外板位置有明显的局部大位移响应;在主甲板的舱口处，出现了明显的局部加速度集中区域。

(3)在船模的一些典型区域，如舷侧外板，局部横向响应也比较明显，主要表现为两侧外板按壳体的呼吸模态振动。尤其艏尖舱壁区域，横向响应很大，加速度已经达到和垂向响应相同的量级。

[1]Mindlin R D，Bleich H H.Response of an elastic cylindrical shell to a transverse step shock wave[J].Journal of Applied Mechanics，1953，20:189 －195.

[2]Haywood J H.Response of an elastic cylindrical shell to a pressure pulse[J].The Quarterly Journal of Mechanics and Applied Mathematics，1958，11:129 －141.

[3]Chertock G.The transient flexural vibrations of ship-like structures exposed to underwater explosions[J].Journal of the Acoustical Society of America，1970，48(l):170 －180.

[4]Geers T L.Residual potential and approximate methods for three-dimensional fluid-structure interaction problems[J].The Journal of the Acoustical Society of America，1971，49:1505－1510.

[5]Geers T L.Doubly asymptotic approximations for transient motions of submerged structures[J].The Journal of the Acoustical Society of America，1978，64:1500－1508.

[6]Geers T L，Felippa C A.Doubly asymptotic approximations for vibration analysis of submerged structures[J].The Journal of the Acoustical Society of America，1983，73:1152 －1159.

[7]Ergin A.The response behaviour of a submerged cylindrical shell using the doubly asymptotic approximation method(DAA)[J].Computers and Structures，1997，62(6):1025－1034.

[8]Liang C C，Hsu C Y，Lai W H.A study of transient responses of a submerged spherical shell under shock waves[J].Ocean Engineering，2000，28:71 －94.

[9]刘建湖.船舶非接触水下爆炸动力学的理论和应用[D].无锡:中国船舶科学研究中心，2002.LIU Jian-hu.Theory and its applications of ship dynamic responses to non-contact underwater explosions[D].Wuxi:China Ship Scientific Research Center，2002.

[10]姚熊亮，孙士丽，陈 玉，等.非线性双渐进法应用于水中结构瞬态运动的研究[J].振动与冲击，2010，10(29):9－15.YAO Xiong-liang，SUN Shi-li，CHEN Yu，et al.Transient motions of submerged structures with nonlinear fluid-structure interaction method [J].Journal of Vibration and Shock，2010，10(29):9 －15.

[11]Cole R H.Underwater explosion[M].New Jersey:Princeton University Press，1948.

[12]Keil A H.The response of ships to underwater explosions[J].Transactions of the Society of Naval Architects and Marine Engineers，1961，69:366 －410.

[13]Rayleigh L.On the pressure developed in a liquid during the collapse of a spherical void [J].Philosophical Magazine，1917，34:94 －98.

[14]Benjamin T B，Ellis A T.Cavitation:The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries[J].Philosophical Transactions of the Royal Society of London，1966，260:221－240.

[15]Plesset M S，Chapman R B.Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary [J].Journal of Fluid Mechanics，1971，47:283 －290.

[16]Gibson D C，Blake J R.The growth and collapse of bubbles near deformable surfaces[J].Applied Scientific Research，1982，38:215－224.

[17]Best J P，Kucera A A.Numerical investigation of nonsphericalrebounding bubbles [J]. JournalofFluid Mechanics，1992，245:137 －154.

[18]Zhang S，Duncan J H，Chahine G L.The final stage of the collapse of a cavitation bubble near a rigid wall[J].Journal of Fluid Mechanics，1993，257:147－181.

[19]Klaseboer E，Khoo B C，Hung K C.Dynamics of an oscillating bubble near a floating structure[J].Journal of Fluids and Structure，2005，21:395－412.

[20]Hicks A N.Explosion induced hull whipping.In:Advances in marine structures(Smith，C.S.，Clarke，J.D.，eds.)[C].Int.Conf.on Advances in Marine Structures.London:Elsevier 1986.

[21]Smiljanic B，Bobanac N，Senjanovic I.Bending moment of ship hull girder caused by pulsating bubble of underwater explosion[J]. In:Faltinsen， O.(Ed.)， Proceedings Hydroelasticity in Marine Technology. A.A.Balkema，Trondheim，1994.pp.149－156.

[22]Zong Z.Dynamic plastic response of a submerged free-free beam to an underwater gas bubble[J].Acta Mechanics，2003，161:179－214.

[23]Zong Z.A hydroplastic analysis of a free-free beam floating on water subjected to an underwater bubble[J].Journal of Fluids and Structures，2005，20:359 －372.

[24]Zhang N，Zong Z.The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble[J].Journal of Fluids and Structures，2011，27:1326－1336.

[25]姚熊亮，陈建平，任慧龙.水下爆炸气泡脉动压力下舰船动态响应分析[J].哈尔滨工程大学学报，2001，42(2):48－55.YAO Xiong-liang， CHEN Jian-ping， REN Hui-long. The analysis of dynamic response of ship hull subjected to gas bubble impulsive pressure of underwater explosions[J].Journal of Harbin Engineering University，2001，42(2):48－55.

[26]李玉节，张孝慈，吴有生，等.水下爆炸气泡激起的船体鞭状运动[J].中国造船，2001，42(3):1－7.LIYu-jie， ZHANG Xiao-ci， WU You-sheng， etal.Whipping response of ship hull induced by underwater explosion bubble[J].Shipbuilding of China，2001，42(3):1－7.

[27]Vermon T A. Whippingresponse ofship hullsfrom underwaterexplosion bubble loading[J]. Technical Memorandum 86/255，Defence Research Establishment Atlantic，1986:1 －41.

[28]Deruntz J A，Geers T L.Added mass computation by the boundary integral method[J].International Journal for Numerical Methods in Engineering，1978，12:531－550.