基于两阶段学习的半监督SVM故障检测方法

陶新民，曹盼东，宋少宇，付丹丹

(哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001)

故障检测就是对测取的含有故障信息的信号利用信号处理和分析技术，找出和故障有关的特征参数并利用这些特征参数对设备的实时技术状态进行判别。这里涉及到两个方面的问题，一是利用信号处理技术进行特征提取;二是利用模式识别技术进行故障检测。在信号特征提取方面，主要分为:信号的时域特征，如信号的均值、均方值、峰值、峭度和歪度等;信号频域特征，如能量谱、AR功率谱等;以及信号的时频特征，如小波分析，Hilbert变换和短时傅里叶变换等[1]。

在模式识别方法方面，支持向量机算法(SVM)因其良好的非线性区分能力，已广泛应用到故障检测领域[2－5]。支持向量机主要思想是建立一个最优决策超平面，使得该平面和最近的两类样本(即支持向量)之间的距离最大化，从而避免以往神经网络学习出现的过拟合、易陷入局部极值和维数灾难等诸多问题。但是，传统基于支持向量机的故障检测方法[3－6]只能使用样本集中的已标识样本进行学习，而在轴承故障检测领域，人工标识样本的代价太大，因此只有少数样本是标识过的，大量的是未标识的样本。而传统的SVM方法作为一种监督检测算法，需要一定数量且属于不同类别的标识样本进行训练才能获得较好的故障检测能力。如今，一种联合标识样本和未标识样本的半监督学习方法吸引了众多科学工作者的目光，并逐渐成为当前机器学习领域的研究热点[7－9]。

半监督学习是将已标识样本和未标识样本提供的聚类信息结合起来，进而提高算法的分类精度。因此，可以说，半监督学习方法较传统分类算法更有助于解决实际问题。目前，结合未标识样本信息来提高SVM算法的性能也有一些文献提出，如 Joachims在文献[10]中提出了直推式支持向量机(TSVM)，加入了未标识样本形成的规划项，引导分类超平面通过低密度区，减小错分的概率，但同时带来了非凸优化的问题;Mikhail等[11]提出了LapSVM算法，考虑了样本集的内部结构，但由于半正定优化问题同样导致该算法易陷入局部解。为了能更好地利用未标识样本信息来提高SVM算法性能，本文提出一种基于两阶段学习的SVM算法并将其应用到故障检测领域。该算法首先在利用基于图的半监督模型给未标识样本加以伪标识;随后将这些伪标识样本与标识样本作为整个训练样本集，输入到SVM算法中进行训练学习，使得SVM算法在训练时能充分考虑未标识样本带来的结构信息，进而提高算法的分类精度。考虑到伪标识生成过程中可能会有噪声，在SVM训练前根据k近邻图，对比样本标识值识别噪声样本并删除，针对剩下的每个样本根据其所属类别的概率设置不同的惩罚因子，来增强SVM算法的鲁棒性和抗干扰能力。实验部分将本文提出的基于两阶段学习的半监督SVM算法应用到故障检测领域同其他SVM算法进行对比，结果说明本文算法在只有少量标识样本的情况下故障检测精度较其他算法有较大幅度提高。

1 传统的支持向量机分类算法

支持向量机算法是建立在统计学习理论中结构风险最小化原理基础上，根据有限的样本信息，在模型复杂度和学习能力之间寻求最佳匹配，以期获得最好的泛化能力。它通过核函数将原始特征空间中的非线性分类界面映射到更高维的特征空间中，使得分类界面在高维特征空间中变得线性可分，使分类效果更好。

其过程可表述为，对于n个样本的二分类问题，假设{(x1，y1)，(x2，y2)，…，(xn，yn)}为给定的训练样本和其期望输出，寻找最优权值向量w和阈值b，使下面的代价函数最小化[12]。

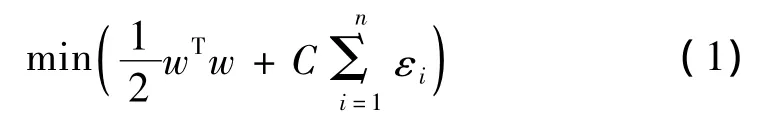
约束条件:

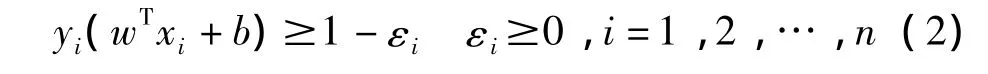
式中:C＞0是惩罚因子，表示对错分样本的惩罚程度，εi为松弛变量，表示对训练样本的错分程度。可以利用拉格朗日乘子法求解该问题的最优解，从而确定最优分类。

为了测试较少标识样本对SVM分类器性能的影响，选用月牙形样本集，该样本集共200个:类1有104个;类2有96个。SVM算法的参数设置为:高斯核函数，核宽度0.35，惩罚因子C=1 000，已标识的训练样本数为10个，类别比例定为6∶4，分别用菱形和实心圆表示，未标识样本为190个，用正方形虚框表示，训练后得到的SVM最优分类界面如图1所示。

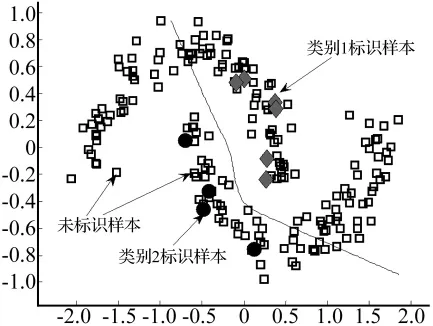
图1 传统SVM分类器得出的分类界面Fig.1 The classification interface after using the traditional classifier

从图1可以看出，由于训练样本中标识样本太少，提供的样本集信息太少，无法准确代表整个样本集合的样本分布信息，只依靠这些标识样本，训练出的SVM分类器泛化性能并不理想。因此传统SVM分类算法在标识样本较少时得到的分类器泛化性能较差，而这种缺乏样本标识的情况在现实中是普遍存在的，因此如何提高标识样本较少情况下的SVM分类器泛化性能是值得深入研究的。

2 基于两阶段学习的半监督SVM算法

为了能将未标识样本的聚类信息[13]纳入到训练过程，进而提高SVM算法的分类精度，本文提出一种基于两阶段学习的半监督SVM分类算法。算法首先利用基于图的半监督模型给未标识样本以伪标识，然后将这些伪标识样本和标识样本共同输入到SVM算法中，使得SVM算法在训练阶段能得到更全面的样本集合信息，进而提升算法的分类性能。

2.1 算法中的伪标识生成

伪标识的生成主要分为两步:构建图模型，根据某种距离度量计算相似度矩阵;依据概率转移矩阵生成伪标识[14]。

2.1.1 确定相似度矩阵

假设训练样本特征x为d维向量，y为样本x的标识值，样本总数为n:n=l+u。其中前l个为已标识样本，样本特征和对应标识值构成的样本集合为L:L={(x1，y1)，(x2，y2)，…，(xl，yl)};后 u 个为未标识样本，样本特征和对应标识值构成的样本集合为U:U={(xl+1，yl+1)，(xl+2，yl+2)，…，(xl+u，yl+u)}，则整体训练样本集合为S:S=L∪U。

利用基于欧氏距离的高斯函数构建相似度矩阵W。为方便矩阵运算，将矩阵W分割成四个子矩阵，如式(3)所示，其中Wll为已标识样本间的相似度矩阵，Wlu为已标识样本和未标识样本间的相似度矩阵，Wul为未标识样本和已标识样本间的相似度矩阵，Wuu为未标识样本间的相似度矩阵。

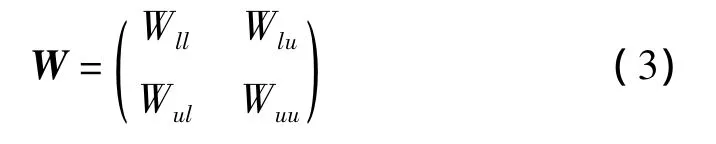
2.1.2 依据转移概率确定伪标识

定义标识转移概率Tij，表示标识从第j个样本转移到第i个样本的概率。其具体表示形式见式(4)。

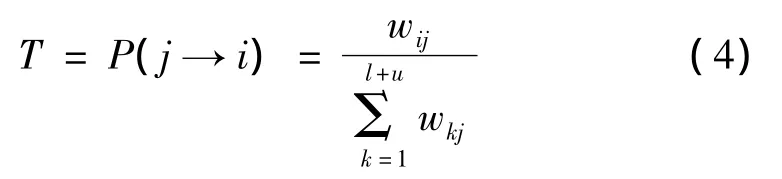
其中:wij表示相似度矩阵W中第i个样本和第j个样本间?的相似度表示第j个样本和其他所有样本间的相似度总和。

同时定义标识矩阵Y∈R(l+u)*N，N代表总类别数，Y的每行代表样本点xi属于每一类的概率，其中未标识样本属于每一类的初始概率定为1/N，表示其所属类别待确定。

伪标识生成基本步骤为:传递标识Y←YT;行单位化Y;固定标识样本，重复执行传递，直到Y收敛。为方便计算，将矩阵分割为:

可导出未标识样本的伪标识矩阵为:

式中I为单位阵。则伪标识样本点的预分类为:

式中:ciu为伪标识样本集中第i个样本所属的类别，yuij为伪标识样本中第i个样本属于第j类的概率，此处i=l+1，l=2，…，l+u，j=1，2，…，N。

图2为伪标识生成后，利用本文算法训练得出的分类界面，其中加号表示类别1伪标识样本，菱形框表示类别2伪标识样本。

图2 伪标识生成情况和分类界面Fig.2 The classification interface and the of producing circumstance pseudo labels

由图2可以看出本文提出的两阶段学习模型，能充分发掘整体样本集的分布信息，利用已有的标识样本信息对未标识样本进行伪标识，从而得到更多的训练样本，这样使得SVM分类器在训练时能兼顾全局聚类信息，而不会陷入局部最优解，得出的分类器反映了整体样本集的分布结构，最终提高了SVM分类器的泛化性能。同时本文算法还需能对边界噪声样本进行处理，以避免标识穿越低密度区导致错传的情况，最大程度地保证SVM分类器在训练时能得到更多更准确的样本集信息。

2.2 算法中核宽度的确定

在伪标识生成过程中，相似度矩阵W中的核宽度δ以往都是通过反复实验得出的，增加了其计算时间和复杂度，为此本文采用自适应调节的方法。

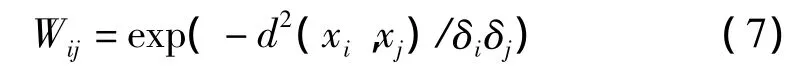
2.3 对伪标识样本进行去噪处理

生成的伪标识样本中可能存在边界噪声样本，将导致SVM算法得到的信息有偏差，致使最终训练出的SVM算法分类能力被削弱，因此需要对伪标识样本进行去噪处理。本文采取两种方法，第一种通过对比标识值，识别并删除噪声样本，第二种根据样本所属类别的信任度设置不同的惩罚因子。

将相似度矩阵W转换成k近邻图相似矩阵W*，以表征样本间的聚类结构信息。根据k近邻图稀疏矩阵，对比样本点和其近邻点的标识，如果某样本点的标识值和其近邻点的伪标识值不相同，需判断该样本是否为噪声样本。令下式:

其中:yu是未标识样本点的伪标识矩阵。W*是k近邻图相似矩阵，则伪标识样本点的预分类变为:

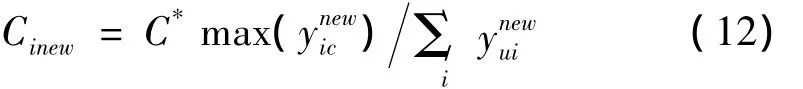
2.4 基于两阶段学习半监督SVM故障检测算法流程

本文将上述基于两阶段学习的半监督SVM算法应用到故障检测中，具体步骤如下:

(1)首先根据相应的故障特征提取方法计算出特征向量，将标识样本和未标识样本组合成样本集合;

(2)计算样本集的相似度矩阵W并变换成k近邻图相似矩阵W*，相似度计算时采用高斯核参数，其参数选择采用的是平均7近邻距离法;

(3)确定标识转移概率矩阵T，计算未标识样本的伪标识矩阵yu;

(4)利用公式(10)和(11)去除噪声样本，得到新的样本标识矩阵

(5)用公式(12)计算每个样本的惩罚因子Cinew，将处理后的样本集(xi)及参数Cinew代入到SVM的优化函数(1)中，K(xi，xj)选用高斯核函数，核参数与相似度矩阵W的参数取值相同;

(7)对于新的采样信号，计算其特征值，然后输入到决策函数进行故障检测判断。

3 试验分析

3.1 特征提取

本文采用的试验样本来自美国Case Western Reserve University电气工程实验室[15]。振动信号的收集来自安装在感应电机输出轴支撑轴承上端机壳上的振动加速度传感器。实验模拟了滚动轴承的4种运行状态:①正常运行状态;②外圈故障;③内圈故障;④滚动体故障。

本文采用基于相空间重构(RPS)模式的特征提取方法，其中相空间重构的参数包括嵌入维数m和延迟时间间隔τ。选用训练样本易得的正常样本相空间的投影系数作为故障特征，即首先确定正常样本相空间的参数，然后取其他类型的样本在该空间的投影系数作为故障检测的特征[2]，具体描述如下:

若轴承振动信号时间序列为:

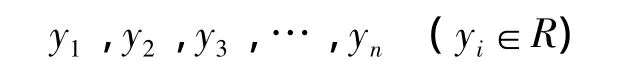
当正常样本相空间的嵌入维数为m，延迟时间间隔为τ，则采用时间延迟技术重构相空间为:

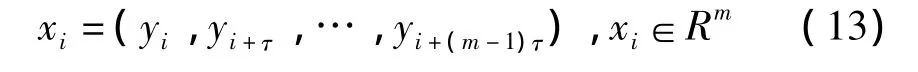
式中:xi为信号在重构相空间的投影系数，其中相空间的参数利用互信息函数指标来确定，嵌入维度选择文献[2]提供的方法。试验确定的正常样本相空间的延迟间隔τ等于2，嵌入维度m等于5，因此故障检测的特征为5维矢量。最终形成正常样本、内圈故障样本、外圈故障样本和滚动体故障样本四种5维矢量作为故障检测特征。

3.2 故障检测试验对比

选择前面生成的1 000个正常样本、1 000个内圈故障样本、1 000个外圈故障样本和1 000个滚动体故障样本组成训练集合，同样分别选择1 000个样本组成测试样本集合。有标识样本集大小从100到500，间隔为50进行变化。将本文的基于两阶段学习的半监督支持向量机算法(TSLSVM)同支持向量机算法(SVM)，模糊支持向量机算法(FSVM)，直推式支持向量机算法(TSVM)，拉普拉斯支持向量机算法(LapSVM)进行比较学习。

实验迭代次数为20次，取20次的平均值作为最终的结果。SVM中核函数为高斯函数，采用10次交叉验证法选择最佳的核宽度为0.35，惩罚因子为 C=1 000，拉格朗日因子λ=10－7;本文算法中k近邻图的近邻数选为7;TSVM中惩罚函数C=1/2λ，核函数为径向基函数，核宽度为0.35;FSVM算法的模糊度计算中，近邻数K值为9，模糊度为1;LapSVM中RKHS(再生核希尔伯特空间)规划因子γA=10－5，流行规划因子γI=1，近邻数 NN=7。

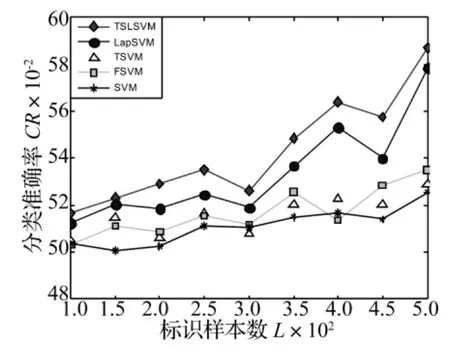
图3 不同标识样本数目下的内圈故障检测率Fig.3 Plot of inner fault detection rate under labeled samples with different sizes

图4 不同标识样本数目下的外圈故障检测率Fig.4 Plot of outer fault detection rate under labeled samples with different sizes

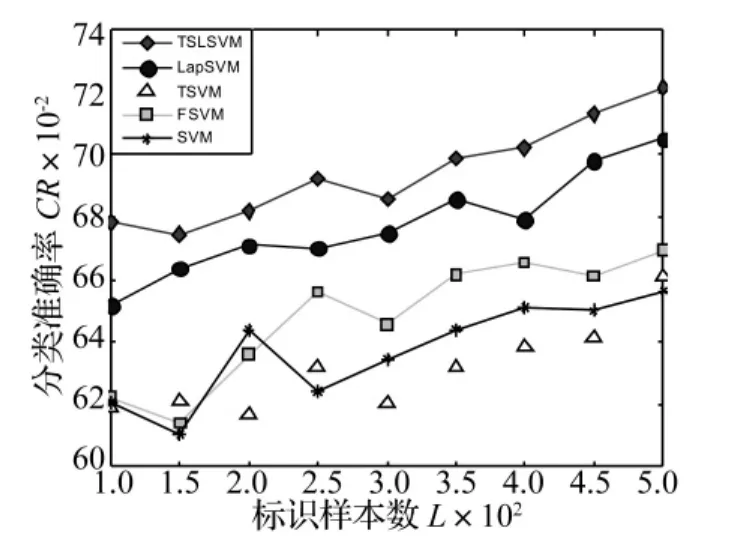
图5 不同标识样本数目下的滚动体故障检测率Fig.5 Plot of ball fault detection rate under labeled samples with different sizes

试验结果如图3～5所示，其中图3为内圈故障的检测结果，图4为外圈故障检测结果，图5为滚动体故障检测结果。从这些实验结果可以看出，随着标识样本数目的增多，各种算法的检测性能也随之增强，另外本文算法在不同数目的标识样本集合下检测性能都好于其他算法，这是由于本文算法是一个半监督算法，它充分考虑到了未标识样本集合提供的聚类结构信息，因此检测性能大大提高。LapSVM因其本身的半正定优化问题，使算法易陷入局部解，导致检测效果不理想。TSVM由于在引入未标识样本的信息时产生了非凸优化问题，使算法易陷入局部极小解，最终的检测结果不如人意。FSVM算法对边缘噪声过于敏感，检测精度受到了很大的影响。

3.3 含和不含测试样本的本文半监督检测算法性能的比较试验

为了验证本文方法在考虑测试样本信息下的故障检测性能，将测试样本集合加入到本文的训练方法中，作为未标识样本集共同参与分类器的训练学习，其他参数设置同上，同不含测试样本的本文故障检测方法进行比较，结果如图6～8所示。

从实验结果可看出，对于不同类型故障检测性能，相同情况下，增加未标识样本的数目使检测精度平均提高了1%～2%。这是由于将大量的测试样本加到未标识样本集合中，使得半监督学习算法能更加充分地利用它们提供的样本空间聚类信息，尽可能发掘样本集内在的分布信息，使得SVM在训练学习时能提取到更多的样本特征信息，计算出来的流行结构更加精确，更能准确模拟出样本间的结构，使得最终训练出的分类界面更加精确，因此检测性能会大大提高。

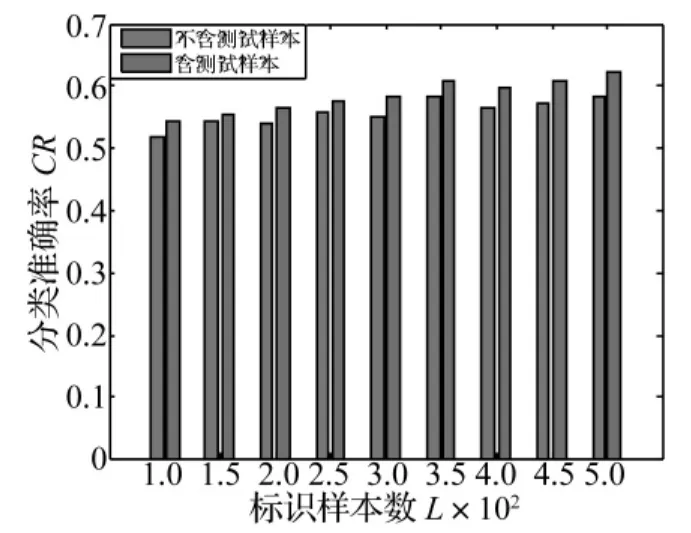
图6 含和不含测试样本对内圈故障检测结果对比Fig.6 Comparison of inner fault detection of the proposed method with test data and without test data

图7 含和不含测试样本对外圈故障检测结果对比Fig.7 Comparison of outer fault detection of the proposed method with test data and without test data

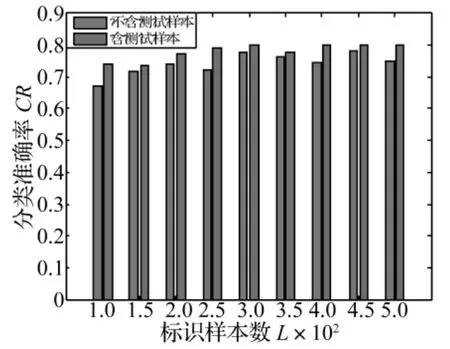
图8 含和不含测试样本对滚动体故障检测结果对比Fig.8 Comparison of ball fault detection of the proposed method with test data and without test data

3.4 k值对本文算法的影响

为了测试k近邻图相似矩阵中不同近邻数k值对本文算法性能的影响，将 k 值取为 2，4，6，8，10，12，14。标识样本数目选择100∶500，间隔为50，取不同数目标识样本集训练后的平均结果，针对三种不同故障检测类型进行实验对比，其他参数同上，结果如图9所示。

图9 不同k值对检测性能的影响Fig.9 The effect of different k value on performance

由实验结果可以看出k设置在6～11处即可，分类精度在此区间时比较好而且较稳定。k选取太小就成了最近邻法，如果样本集合分散度高的话，得出的参数不能很好的代表相似样本间的相似信息;k值过大时有可能将类别外的样本纳入其中，带来了类间的相互干扰，导致最终分类精度呈下降趋势。

4 结论

本文提出了一种基于两阶段学习的半监督SVM故障检测方法。该算法首先利用基于图的半监督模型，预先给未标识样本进行伪标识，接着利用k近邻图将其中的噪声样本识别并删除，然后将处理后的样本集当成已标识样本集交由SVM处理，使SVM算法充分考虑整个样本的分布信息，最终提高故障检测率。仿真试验结果表明本文方法在不同比例的标识样本集合情况下，故障检测性能优于其他算法。另外，本文对含有测试样本和不含测试样本的情况进行了比较，结果表明含有测试样本学习的检测性能较不含测试样本好。由于未标识样本在故障检测领域很容易得到，因此本文方法具有很好的现实应用价值。需要说明的是，本文算法并未对未标识样本集中存在的不均衡样本分布情况进行分析，这也是本课题下一阶段深入研究的重点。

[1]陶新民，徐 晶.基于紧密度FSVM新算法及在故障检测中的应用[J].振动工程学报，2009，22(4):418 －424.

[2]陶新民，刘福荣.不均衡样本下基于SVM的故障检测新算法[J].振动与冲击，2010，29(12):8－12.

[3]明 阳，陈 进.基于谱相关密度切片分析和SVM的滚动轴承故障诊断[J].振动与冲击，2010，29(1):197－201.

[4]黄红梅，袁慎芳.基于光纤Bragg光栅和支持向量机的冲击损伤识别研究[J].振动与冲击，2010，29(10):54－59.

[5]张 超，陈建军.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击，2010，29(10):217－221.

[6]Lin C F，Wan S D.Fuzzy support vector machines[J].IEEE Trans.on Neural Networks，2002，13(2):464 －471.

[7]Zhu X.Semi-supervised learning litertures survey[D].Technical Report 1530，Computer Science，University of Wiscinsin-Madison，2005:18－25.

[8]Bai S H.Semi-supervised learning of language model using unsupervised topic model[C].IEEE International Conference on Acoustics， Speech and Signal Processing-Proceedings，2010:5386－5389.

[9]Mehdizadeh M，MacNish C.Semi-supervised neighborhood preserving discriminant embedding:a semi-supervised subspace learning algorithm[J].Computer Science，2011，6494:199－212.

[10]Joachims T.Transductive inference for text classification using support vector machines[C].Proc.16th International Conf.on Machine Learning，1999:200 －209.

[11]Belkin M，Niyogi P.Manifold regularization[J].Machine Learning Research，2006，7(8):31－42.

[12]Cortes C，Vapnik V.Support vector networks[J].Machine Learning，1995，7(3):273 －297.

[13]Zhu X， GhahramaniZ. Semi-supervised Learningwith Gaussian fields and harmonic functions[C]//Proceedings of the Twentieth International Conference on Machine Learning.Washington DC，USA，2005:5－12.

[14]Zhu X，Ghahramani Z.Learning from labeled and unlabeled data with label propagation[D].Technical Report CMUCALD－02－107，Carnegie Mellon University，2002:1－7.

[15]These data comes from Case Western Reserve University Bearing Data Center Website[OL].http://www.eecs.cwru.edu/laboratory/bearings/.lobal information of the whole samples can be considered by SVM to enhancet