我国区域气候因素影响下的男性收缩压参考值

张明鑫 葛 淼 张云霞 周文华 (陕西师范大学旅游与环境学院，陕西 西安 70062)

气候作为人类赖以生存的自然环境的一个重要组成部分，它的任何变化都会对自然生态系统以及社会经济系统产生影响。全球气候变化的影响是全方位的、多尺度的和多层次的，既包括正面影响，同时也包括负面效应。但目前它的负面影响更受关注，因为不利影响可能会危及人类社会未来的生存与发展。随着全球气候的变化，越来越多的人开始关注人体指标和环境的关系，关于环境、气候因素与血压的关系近年来也有一些报道。但是，对收缩压参考值与气候因素的相关性进行系统性的分析研究，国内外未见报道。为制定中国老年男性收缩压参考值的统一标准，很多人测定了本地区人口的收缩压参考值〔1～11〕。本文用多元线性回归分析和主成分分析的方法研究中国各地测定的老年男性收缩压参考值与气候因素的关系。

1 资料与方法

1.1 一般资料 检索中国期刊网全文数据库等。在西安、北京、上海、青海、西藏、重庆等地相关医院购买有关资料。收集了中国30个省、市、自治区(缺乏西藏、台湾省、香港特别行政区、澳门特别行政区的资料)。医院和有关研究单位利用动态血压仪(型号ICR5300型)测定的3 265例健康男性收缩压参考值;年龄范围45～60岁。

1.2 气候因素 气候因素取材于有关地理著作和辞典〔12〕，选取的气候因素指标是:海拔高度(X1)，年日照时数(X2)，年平均气温(X3)，年平均相对湿度(X4)和纬度(X5)。

海拔高度(X1):长时期观测海水水位而确定的海水面平均位置，叫做平均海水面，通常作为高程的基准面。某一地点高出平均海水面的垂直距离叫做海拔高度，以米(m)为单位。

年日照时数(X2):一地太阳的中心从东面地平线出现到进入西面地平线为止的时间，称为可照时间，以小时(h)为单位。

年平均气温(X3):气温是指离地面1.5 m高的百叶箱内测得的空气温度。在一天24 h内定时观测的气象台站，以摄氏度(℃)为单位。

年平均相对湿度(X4):空气中的实际水汽压与当时气温下的饱和水汽压之比称为相对湿度，以百分数(%)为单位。

纬度(X5):是指某点与地球球心的连线和地球赤道面所成的线面角，其数值在0至90°。

1.3 统计学分析 采用SPSS17.0软件进行相关分析。

2 结果与讨论

2.1 男性收缩压正常参考值与气候因素的相关分析 把男性收缩压正常参考值作为因变量(YSBP)，九项地理指标作为自变量，运用SPSS17.0统计软件中的相关分析方法得出九项地理指标与男性收缩压正常参考值YSBP之间的相关程度，并对其进行假设检验，即简单相关系数r。计算得到男性收缩压正常参考值与各个地理指标之间的单相关系数r及显著性(P)分别为:r1= －0.429(P1=0.018)，r2=0.233(P2=0.215)，r3=－0.078(P3=0.681)，r4=0.069(P4=0.719)，r5=0.282(P5=0.131)。

2.2 男性收缩压正常参考值的多元线性回归分析 在复杂的地理环境中，某些要素的变化很难预测与控制，相反有些要素比较容易得到。因此，在这些难预测的要素与其他比较易得的要素之间建立一种近似的函数表达，就可以比较容易地通过简单易得要素掌握和了解那些难以控制的要素的变化情况。

以九项地理指标作为自变量，城市男性收缩压正常参考值Y作为因变量，运用SPSS17.0中的向后消元法对其做多元回归分析，得到的方程为:YSBP=104.211－0.003X1+0.004X2+0.048X4±6.94(标准差)

其中拟合优度R2=0.338，F统计量的观察值为5.932，显著性概率P=0.000。

2.3 城市男性收缩压正常参考值的曲线估计 在复杂的地理环境中，要素之间除了线性关系外，非线性关系也是大量存在的，有些非线性关系可以利用图形表示为曲线。因为非线性关系无法直接建立线性回归模型，所以通过某种变换或者变量替换，把非线性关系转换为新变量下的线性关系〔13〕。同时可以运用建立线性回归模型的方法，建立要素间的非线性回归模型。本文利用SPSS17.0软件分别对老年男性收缩压四项指标的正常参考值和气候因素进行曲线估计。SPSS17.0软件中曲线估计模块所用到的曲线方程如下:①拟合对数曲线模型(Logarithmic):Y=b0+b1lnx;②拟合倒数曲线模型(Inverse):Y=b0+b1/x;③拟合二次曲线模型(Quadratic):Y=b0+b1x+b2x2;④拟合三次曲线模型(Cubic):Y=b0+b1x+b2x2+b3x3;⑤拟合复合曲线模型(Compound):Y=b0×b1x2;⑥拟合幂函数曲线模型(Power):Y=b0x3;⑦拟合S形曲线模型(S):Y=e(b0+b1/x);⑧拟合增长曲线模型(Growth):Y=e(b0+b1x);⑨拟合指数曲线模型(Exponential):Y=b0eb1x;⑩拟合Logistic曲线模型(Logistic):Y=1/(1/u+b0×bx1)。

把相关分析中显著性最好的气候因素X1作为自变量，城市男性收缩压正常参考值作为因变量，在SPSS17.0软件中选择系统默认的所有模型对其进行曲线估计，得到的模型摘要和参数评估见表1。

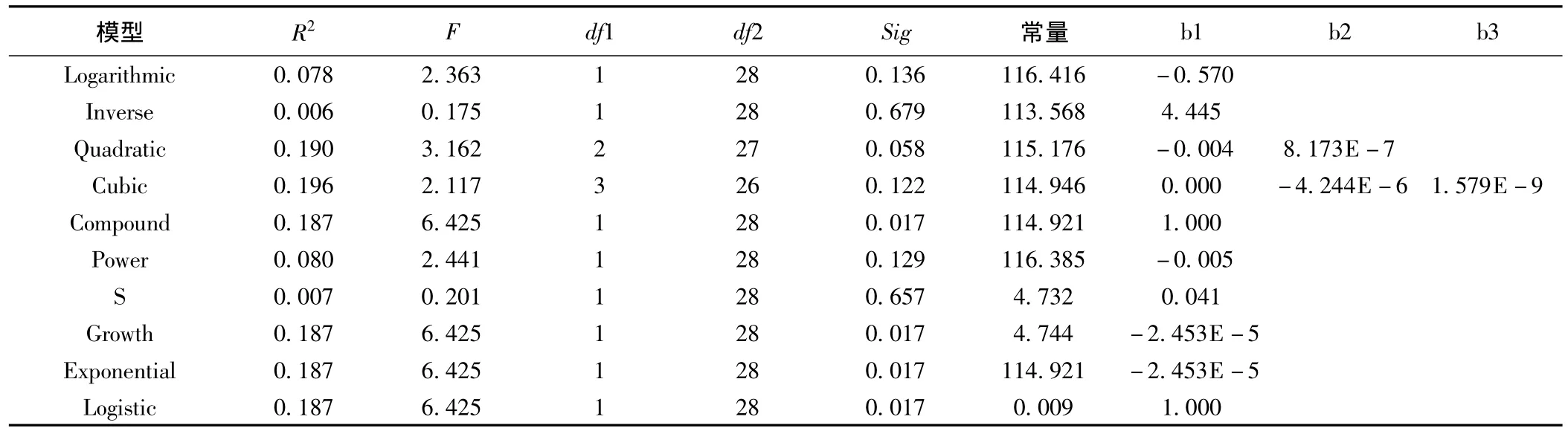
表1 城市男性收缩压正常参考值模型摘要和参数估计

从表1中可以看出解释量(R2)比较高的是三次曲线模型(Cubic，R2=0.196)和二次曲线模型(Quadratic，R2=0.190);最低的是S曲线模型(Inverse，R2=0.007)。由拟合优度来讲三次曲线的拟合优度最好，应该选择该模型，综上分析在这里选择三次曲线模型，得到的非线性回归方程为:

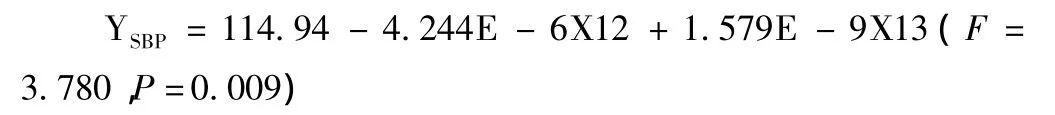
2.4 男性收缩压正常参考值的最优模型选择 应用SPSS17.0软件对男性收缩压正常参考值的三种预测模型进行成对样本双侧T检验，结果见表2。在95%的显著性水平下，多元线性回归模型预测值与实测值之间无显著差异，因此本文选取多元线性回归分析模型作为男性收缩压正常参考值的最优预测模型。

表2 男性收缩压正常参考值实测值与预测值T检验结果

2.5 男性收缩压正常参考值的空间分布制图 为了能更清楚地表示出收缩压正常参考值的地理空间分布趋势，本文选取中国全国范围内县级以上行政单位作为观测点，借助ArcGIS软件中的空间分析模块，精确地拟合并绘制出收缩压正常参考值的地理分布趋势图。

图1 我国男性人口收缩压参考值地域分布规律图

老年男性收缩压正常参考值选择的最优模型是:YSBP=104.211－0.003X1+0.004X2+0.048X4±6.94。

根据该模型预测出中国各个地区的健康男性的收缩压正常参考值，精确地拟合并绘制出男性的收缩压正常参考值的空间趋势分布图。见图1。

由图1能清楚地看出男性收缩压正常参考值的分布趋势，颜色较深的地区正常值比较大，颜色较浅的地方正常值较小;在同一条等值线上的值相同。男性的收缩压正常参考值受海拔高度的影响比较大，分布总体呈现出西北小于东南、内陆小于沿海的趋势。

1 吴升平，王文志，郭玉祥，等.人群高血压干预效果评价〔J〕.中国慢性病预防与控制，1992;1(1):10-20.

2 张维忠，龚兰生，陆 华.动态血压参数的短期重复性研究〔J〕.中华心血管病杂志，1994;22(1):20-4.

3 李昌棣，李梅兰，林利雅，等.24小时人体动脉血压的动态观察〔J〕.暨南大学学报，1990;11(2):14-25.

4 朱广瑾.中国人群生理常数与心理状况〔M〕.北京:中国协和医科大学出版社，2000:219-70.

5 王凤楼，李栋燕，李秀英.尿钠和血压相关的调查研究〔J〕.哈尔滨医科大学学报，1983;1(2):21-6.

6 王长松.武汉市1 121名干部体检血压分析〔J〕.武汉医学杂志，1984;8(4):20-6.

7 侯桂芝，吕瑞秀，裴淑凡，等.由挠动脉血压推算肱动脉血压的测量〔J〕.实用护理杂志，1992;8(5):14-8.

8 刘敏晶，叶洛莉，邓宪风，等.飞行人员体重与血压、血脂及血糖关系探讨〔J〕.医学信息荟萃，1993;6(3):22-6.

9 陈文彬，潘祥林，康熙雄，等.诊断学〔M〕.第6版.北京:人民卫生出版社，2005:558-9.

10 阎崇年，颜吉鹤，宋俊岭，等.中国市县大辞典〔M〕.北京:中共中央党校出版社，1991:1-1446.

11 颜 宏，沈国权，毛耀顺，等.中华人民共和国气候图集〔M〕.北京:气象出版社，2002:2-250.

12 赵 济，陈传康，伍光和，等.中国地理〔M〕.北京:高等教育出版社，2005:3-391.

13 Fiori G，Facchini F，Pettener D.Relationships between blood pressure，anthropometric characteristics and blood lipids in high-and low-altitude populations from Central Asia〔J〕.Ann Hum Biol，2000;27(1):19-28.