姿态机动中SGCMG的一种改进奇异鲁棒操纵律设计*

牟 夏，宗 红，雷拥军

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

姿态机动中SGCMG的一种改进奇异鲁棒操纵律设计*

牟 夏1，2，宗 红1，2，雷拥军1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

单框架控制力矩陀螺（SGCMG）在卫星姿态控制中以其具有大力矩输出能力而受到重视并已成功应用于在轨卫星，其应用难点是构形奇异问题，特别是在快速连续机动的过程中，CMG框架角必须迅速脱离奇异状态.使用描述CMG输出力矩和期望控制力矩夹角的奇异度量方法，以便在仿真中观察判别CMG构形的奇异程度.着重改进CMG的奇异鲁棒操纵律，应用高斯函数的方法确定鲁棒系数.仿真实例表明，与传统的梯度型零运动相比，该方法可以在卫星的连续快速机动中使CMG系统更为迅速地摆脱奇异，更为快速地完成机动并减小姿态抖动.

单框架控制力矩陀螺；姿态机动；CMG操纵律；奇异鲁棒

随着航天技术的发展和任务要求的增多，卫星的敏捷性能受到各方面的极大关注.国外许多先进卫星都具备了快速机动与快速稳定的敏捷性能，能够实现快速侧摆成像、同轨多条带成像、同轨立体成像的功能，从而提高卫星对地观测的时间分辨率、扩大观测区域以及兼具侦查与测绘的能力［1］.

单框架控制力矩陀螺（SGCMG）因其具有大力矩输出能力和快速响应等特点，适合作为航天器快速机动的理想执行机构.

SGCMG应用于卫星姿态控制的难点是奇异问题.目前，国内外在SGCMG操纵律及奇异规避方面已做了大量研究.文献［2］综述了用于SGCMG奇异规避的主要方法并将其分类，对不同操纵律的性能进行了评价，指出现存SGCMG操纵律或在奇异规避方面性能较差，或由于计算量较大而使得实时性较差.文献［3］从奇异性分析的角度对SGCMG的奇异状态进行了研究，提出了奇异可规避性的判别方法.文献［4］基于小卫星的敏捷性需求，针对金字塔构形的SGCMG提出了一种简化的带零运动的鲁棒操纵律，并结合卫星系统操纵律进行了仿真验证.文献［5］针对SGCMG系统做了大量的原理分析，并参考机械臂奇异问题的结论，给出了判定各种奇异的方法和定理，并对一些操纵律进行了仿真验证.文献［6］详细推导了使用SGCMG的航天器姿态动力学模型，并设计了基于Lyapunov的反馈控制律，给出了仿真结论.文献［7］针对航天器大角度机动、快速多目标指向的问题提出了一种基于饱和约束的控制方法，并对单轴连续机动、三轴姿态机动以及使用CMG作为执行机构的情况进行了仿真.

以上文献对研究SGCMG在航天器姿态控制中的应用有重要的参考价值.但是文献［4］中没有明确卫星系统控制方法；文献［5］中的数学理论和仿真比较部分都很完整，但只是针对SGCMG系统假设期望力矩为常数向量，不考虑卫星系统控制律和姿态机动中变化的力矩指令.所以在对SGCMG操纵律的比较分析方面还可以做更多工作，例如将以上文献中的SGCMG操纵律放在同一卫星姿态控制模型中，在姿态机动的过程中比较其性能等.

本文研究分析SGCMG操纵律和奇异规避方法在航天器姿态控制系统中的表现，研究几种不同操纵律对航天器姿态的影响，针对奇异鲁棒方法进行改进，提出了一种描述SGCMG输出力矩与期望力矩夹角的奇异度量方法，以便更为直观地观察SGCMG构形的奇异程度，并应用于仿真中的阈值判别.本文还提出了一种适应奇异度量变化的鲁棒系数的选择方法.在仿真过程中，针对姿态单步机动和连续机动的情况进行仿真，比较几种方法的性能.

1 基于SGCMG的卫星姿态机动控制问题描述

使用CMG作为姿态执行机构的刚体姿态动力学方程如下：

式中，J为星体的转动惯量阵，ω为星体坐标系下的角速度，ω×为ω的反对称阵，h为CMG群的角动量，τd为空间外力矩.金字塔构形的CMG如图1所示.

图1 金字塔构形示意图Fig.1 Four pyram id-configured SGCMGs

金字塔构形CMG群的角动量

其中：cβ=cosβ，sβ=sinβ，δi为第i个CMG的框架角，h0为单个CMG的角动量大小.图1中的为第i个CMG的框架轴方向，为第i个CMG的角动量方向x、y、z方向.

h的Jacobian矩阵如下：

假设期望CMG输出的力矩为u，则有

其中C+为Jacobian矩阵C的伪逆.对于金字塔构形的CMG系统，C+的存在性由rank（C）决定.当C不满秩时，就无法直接得到有效的框架角操纵律，产生奇异，即：在某一框架角组合下，沿某一方向或者某个平面上无法输出力矩［8］.为此有多种框架角操纵律用于奇异规避.

通常定义奇异度量D=det（CCT），D越接近零，则CMG越接近奇异状态.下面给出几种典型的框架角操纵律：

1）MP逆法

该方法没有奇异回避能力，但其他方法大多基于此种方法改进而成［2］.

2）零运动法

其中En为单位阵，αNM为零运动系数量的梯度.该方法通过执行空转指令以改变框架角，使CMG系统脱离奇异状态［4］.

3）奇异鲁棒法

其中En为单位阵，α为鲁棒系数.该方法通过产生偏差来换取奇异规避的能力.

除了以上操纵律，还有初始框架角选择法、查表法等CMG操纵律，但实际应用的操纵主要是零运动法和奇异鲁棒法的结合或者改进.

2 控制器设计

2.1 控制器最优控制律设计

采用四元数描述航天器姿态运动.动力学方程见式（1）.

运动学方程为

假设卫星受到的空间外力矩为零，则动力学方程可写为

式中τ为卫星系统的控制输入.由基于时间最优的反馈方法［7］有

Li=为限幅函数，e为四元数误差向量，若 qf为期望的终止四元数，则k，c为控制增益，T为积分常数轴允许的最大力矩，Jii为绕主轴的转动惯量，i=1，2，3.

2.2 改进奇异鲁棒操纵律设计

式（8）为SGCMG的奇异鲁棒操纵律的原理公式，其重点在于“何时”引入“何种”程度的偏差以回避奇异，而判断“何时”引入由奇异度量决定，引至“何种”程度由鲁棒系数决定.

通常定义奇异度量D=det（CCT）.这种形式虽然可以准确反映矩阵C的奇异状态，但不能准确反映CMG构形是否奇异.只有当n个CMG产生的力矩都位于同一平面内而期望力矩垂直于这一平面时，才认为CMG发生了奇异.如果CMG奇异，矩阵C必定奇异；反之矩阵C奇异，CMG不一定奇异［9］.因此，从奇异定义出发，定义奇异参数：

式中，uCMG为CMG输出力矩，u为期望力矩，θ为CMG输出力矩与期望输出力矩间的夹角，η为CMG输出力矩与期望力矩间模的比例关系.由此可知，当CMG构形接近奇异时，θ接近90°，η接近0.

文献［4］中使用阈值判断是否引入零运动或奇异鲁棒，例如在奇异度量D＞m时使用MP逆法，而在D≤m时引入零运动或者奇异鲁棒，即

其中cd为一常数.在奇异鲁棒中，显然 α取值越接近0，则由奇异鲁棒操纵律造成的误差越小.在远离奇异状态时，α可以取0，接近奇异时，可以适当增加α，摆脱奇异后再减小α.文献［4］和［9］没有明确α的设置方法，只做阈值或标称参数.现使用高斯函数选取 α：

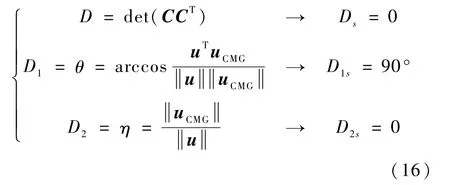
式中，αmax为α的最大值，D为奇异度量，Ds为奇异状态的奇异度量值，若按上文中的奇异度量定义有σ2为方差.当D越接近Ds，α取值越大，服从正态分布.在仿真中，本文给出了以上3种方式的奇异度量曲线用于观测，并使用式（14）的奇异度量方法判定CMG是否引入奇异鲁棒方法计算框架角速度.

3 数值实例

为了比较以上操纵律在姿态机动中的有效性，在此以金字塔构形的4-CMG系统为例，针对几种典型CMG操纵律进行仿真.

选择仿真参数如下：

星体转动惯量

CMG角动量h0=10 N·m·s，金字塔倾角为β= 53.1°，CMG最大输出力矩为τmax=8N·m，U= 8N·m，四元数初值为q=［1 0 0 0］T，角速度初值为ω=［0 0 0］T，增益c=6，k=10.将初始框架角设为δ=［0 90° -90° 0］T.

分别使用梯度型零运动［4］、普通的奇异鲁棒［10］、使用基于式（13）和（14）的奇异鲁棒方法以及使用基于式（15）的改进的奇异鲁棒方法作用于同一卫星控制系统的模型当中，研究姿态机动过程中系统的奇异程度、姿态四元数的收敛趋势和产生的框架角速度指令.具体如下：

（1）梯度型零运动

目标四元数为qf=［0 0 0 1］T，零运动系数为100，仿真时间为150s.仿真得到如下结果，如图2～4所示.

图2 梯度型零运动四元数Fig.2 Quaternions for gradient nullmotion

图3 梯度型零运动奇异度量Fig.3 Singularity measurement for gradient nullmotion

从图2～4可以看出，虽然使用零运动可以完成机动，但是产生了饱和的框架角速度，这种跳变型的指令在具体应用时很难实现，因为现有电机不能产生这种期望的框架角速度.且从图3可以看出，本文提出的奇异度量方法可以更直观的反应CMG构形的奇异程度，可以明显看出直到90s以后，系统完全脱离奇异.

（2）单次机动时，采用新型奇异度量方法的奇异鲁棒与传统奇异鲁棒的对比

目标四元数：qf=［0 0 0 1］T，鲁棒系数α=0.3，仿真总时长为150s，可得如下结果（为对比与传统型奇异鲁棒的区别，图中实线为采用新型奇异度量方法的奇异鲁棒，虚线为传统的奇异鲁棒），如图5～7所示.

在以上仿真的过程中，使用的是阈值判别方法，对于采用新型奇异度量的奇异鲁棒方法，即当夹角D1≥10°或D2≤0.9时，引入奇异鲁棒；在其他时刻，即D1＜10°且D2＞0.9时，使用MP逆法.而对于使用传统奇异度量的奇异鲁棒方法，D≤0.6时，采用奇异鲁棒方法；在其他时刻，即D＞0.6时，使用MP逆法.

对比图5和图2可以看出，使用奇异鲁棒方法可以比零运动方法更为快速地完成机动.

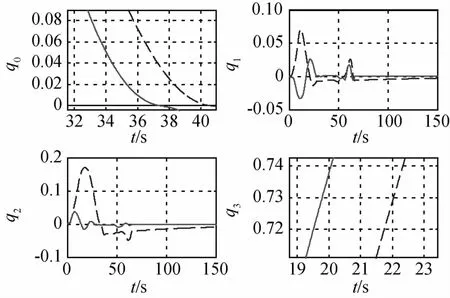
图6 单次机动四元数局部放大图Fig.6 Quaternions for SR in single maneuver（localmagnification）

图7 单次机动框架角速度Fig.7 Gimbal rates for SR in single maneuver

而从图5中实线与虚线的对比来看，采用新型的奇异度量方法可以比采用传统型奇异度量更为快速地完成机动过程，从图6的放大图中可以看出大约提前2s.通过对比q1和q2可以看出使用新型奇异度量的奇异鲁棒方法可以减小四元数的波动.

对比图7与图4可以看出，与零运动方法相比，奇异鲁棒方法可以产生更易跟踪的框架角速度.

（3）连续两次机动时，采用新型奇异度量方法的奇异鲁棒法与传统奇异鲁棒法对比

该仿真中包括两次姿态机动.第一次机动的期望四元数为qf1=［0 0 0 1］T，当 q0达到0（实际取1×10-4）时，认为卫星姿态达到预定位置，可回转，之后期望四元数为：qf2=［1 0 0 0］T.鲁棒系数α=0.3.为着重比较与传统型奇异鲁棒方法的区别，采用和b部分一样的阈值判断法，仿真总时长改为100s，得到如下结果（图中实线为采用新型奇异度量方法的奇异鲁棒，虚线为传统的奇异鲁棒），如图8～10所示.

图8 连续机动奇异鲁棒法四元数Fig.8 Quaternions for SR in continuousmaneuver

图9 连续机动奇异鲁棒法奇异度量Fig.9 Singularity measurement for SR in continuous maneuver

从图8可以看出，经过两次机动的叠加，实线超前虚线约4s时间，并且q1、q2的波动明显减小.

（4）连续两次机动时，采用新型奇异度量方法以及自适应函数的奇异鲁棒法与传统奇异鲁棒法对比

鲁棒系数的最大值αmax=0.3，取奇异度量为模之比D2，根据式（14）鲁棒方法与（3）部分相同，得到如下结果（图中实线为采用新型奇异度量方法并同时采用高斯函数的奇异鲁棒，虚线为传统的奇异鲁棒），如图11所示.

图10 连续机动奇异鲁棒法框架角速度Fig.10 Gimbal rates for SR in continuous maneuver

图11 带有高斯函数奇异鲁棒法四元数Fig.11 Quaternions for SR using Gaussian function

以上的几次仿真中，均使用了同一卫星姿态模型及完全相同的姿态控制律，仅仅对奇异度量和鲁棒系数做了些许改动，对比不同方法的效果.

仿真结果中对比了使用本文提出的利用CMG输出力矩与期望力矩的夹角和模之比来描述系统的奇异程度，如图3和图9.由这些图形可以更有效地得知CMG的构形奇异程度.与传统的奇异度量相比，可以更明显地将奇异状态与非奇异状态区别开来.在图9中，可以看到在姿态机动完成之后，夹角D1≠0且模之比D2≠1，其原因是姿态机动完成之后，计算出的输出力矩和期望力矩的模值非常小，接近于0.从图9中传统的奇异度量曲线来看，采用新的奇异度量方法可以明显抬高奇异度量曲线.

此外，观察图4、图7和图10可以发现，使用了奇异鲁棒方法的系统产生了相对零运动方法更易于跟踪的框架角速度曲线.由于图4中的跳变曲线在实际应用中很难实现，产生可跟踪的框架角速度指令在工程应用中是十分重要的.

4 结 论

本文针对卫星快速姿态机动中CMG框架角操纵律的几种典型方法进行研究分析，提出并在仿真中使用通过描述CMG输出力矩与期望力矩的夹角和模之比观测奇异状态，直观显示CMG奇异程度.此外本文对其中的奇异鲁棒法进行了改进，提出了一种选取鲁棒系数的方法，使得鲁棒系数具有自适应调节能力.仿真表明，在相同的卫星姿态控制模型中，本文所设计的方法可以在卫星的大角度连续摆动过程中使系统更为迅速地脱离奇异，完成姿态机动，并计算出更易跟踪的框架角曲线.对本文所提出的方法进行多次仿真试验，针对初始框架角、初始及目标四元数和鲁棒系数的修改，能够说明本文提出的方法在大角度快速连续姿态机动时更为有效.在不同的初始条件下，仿真参数需要多次修改调试，才能起到较好的效果.由于卫星控制律本身也具有实时调节特性，目前作者尚未找到参数与结果间的线性关系，具体方法有待深入研究.

［1］ 刘一武，张军.敏捷卫星快速姿态机动控制方法研究［C］.全国第十三届空间及运动体控制技术学术年会论文集，宜昌，2008 Liu Y W，Zhang J.Rapid attitude maneuver control for agile satellite［C］.The 13thNational Annual Conference of Space and Vehicle Control Technology，Yichang，2008

［2］ 吴忠，吴宏鑫.单框架控制力矩陀螺系统操纵律研究综述［J］.宇航学报，2000，21（4）：140-145 Wu Z，Wu H X.Survey of steering laws for single gimbal control moment gyroscopt systems［J］.Journal of Astronautics，2000，21（4）：140-145

［3］ 张锦江，李季苏，吴宏鑫，等.大型航天器SGCMG系统的奇异性分析研究［J］.中国空间科学技术，2001，21（3）：36-41 Zhang J J，Li JS，Wu H X.A study on singularity analysis of large spacecraft SGCMG systems［J］.Chinese Space Science and Technology，2001，21（3）：36-41

［4］ 徐开，金光.光学观测卫星姿态的SGCMGs力矩受限控制研究［C］.中国空间科学学会空间机电与空间光学专业委员会2008学术年会，兰州，2008 Xu K，Jin G.Research on optical observation satellite attitude control with torque-limitied SGCMGs［C］.The 2008 Annual Conferenc of Chinese Society of Space Research’Comm ittee for Space Mechaeronics and Space Optics，Lanzhou，2008

［5］ Bedrossian N S.Steering law design for redundant single gimbal controlmoment gyro system［D］.Massachusetts Institute of Technology，1987

［6］ Oh H S，Vadali S R.Feekback control and steering laws for spacecraft using single gimbal control moment gyros［J］.The Journal of Astronautical Sciences，1991，39（2）：183-302

［7］ Bong W.Rapid multi-target acquisition and pointing control of agile spacecraft［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Denver，August 14-17，2000

［8］ 汤亮，陈义庆.单框架控制力矩陀螺奇异性问题研究［J］.航空学报，2007，28（5）：1181-1189 Tang L，Chen Y Q.Research on singularity questions of single-gimbal control moment gyros［J］.ACTA Aeronautica ET Astronautica，2007，28（5）：1181-1189

［9］ 杨雅萍，吴忠.变速控制力矩陀螺模式调度型操纵律设计［J］.空间控制技术与应用，2011，37（6）：9-13 Yang Y P，Wu Z.Mode-scheduling steering law design for variable speed controlmoment gyroscope［J］.Aerospace Control and Application，2011，37（6）：9-13

［10］ Bong W.Singularity robust steering logic for redundant single-gimbal control moment gyros［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Denver，August 14-17，2000

An Im proved Singularity Robust Steering Law for Single-Gim bal Control M om ent Gyros for Attitude M aneuver

MU Xia1，2，ZONG Hong1，2，LEIYongjun1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China）

The single gimbal control moment gyro，used in spacecraft attitude control system，deserves special attention in recent years due to its large control torque.However，the singularity problem is the major constraint on rapid attitudemaneuver，especially in a continuousmaneuver process，the spacecraft should escape from singularity rapidly.In this paper，based on the angle between desired control torque and output torque from CMG，a new singularity measurement is introduced.An improved singularity robust steering law are proposed，and a Gaussian function is adopted to determine the singularity robust coefficient.Simulation results demonstrate that compared with the traditional gradient nullmotion method，the proposed algorithm can finish attitude maneuver more quickly.It assures the singularity-escape more rapidly and reduces attitude chattering magnitude.

single gimbal controlmoment gyros；attitude maneuver；CMG steering law；singularity robust

V448.2

A

1674-1579（2012）02-0017-07

牟 夏（1987—），女，硕士研究生，研究方向为航天器姿态控制；宗 红（1971—），女，研究员，研究方向为航天器制导、导航与控制；雷拥军（1971—），男，高级工程师，研究方向为复杂航天器姿态控制.

*国家自然科学基金资助项目（60804016）.

2011-09-14

DO I：10.3969/j.issn.1674-1579.2012.02.004