全系数自适应控制器若干稳定性质分析*

王 勇

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190）

全系数自适应控制器若干稳定性质分析*

王 勇1，2

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190）

在更加一般的条件下对黄金分割反馈控制器在单输入单输出和多输入多输出特征模型中的稳定性和鲁棒性进行了系统分析，并在混合辨识背景下研究了投影梯度法在特征模型框架中应用时的输入状态稳定（ISS）性和参数估计误差的L2界.最终的结果进一步扩展了已有的结论，对整个系统的稳定性分析具有重要作用.

全系数自适应控制；特征模型；黄金分割；梯度法

基于特征模型的全系数自适应控制器包括：维持跟踪控制器、黄金分割控制器、逻辑积分和逻辑微分控制器等，其中黄金分割控制器在自适应过程的初始阶段起着重要作用，而投影梯度法由于其操作简单、收敛过程较为平稳成为自适应律的首选方法，两者在全系数自适应控制中起着重要作用.黄金分割控制方法是吴宏鑫院士在1986年炼油厂加热炉温度控制工程实际中发现的，经过大量实际控制工程应用考验，于1990年发表于“全系数自适应控制理论及其应用”专著之中，1992年解永春博士从理论上首次证明了在参数估计收敛后这种黄金分割控制器组成的闭环系统的稳定性［1］，1994年证明了黄金分割自适应控制器的稳定性和鲁棒性［2］，2000年齐春子博士又进一步证明了二阶多变量黄金分割自适应控制的稳定性［3］，2005年孙多青博士后更进一步证明了三阶/四阶情况下的稳定性［4］.从工程实际和一系列的稳定性分析中可以发现，黄金分割控制器和投影梯度法自适应律在基于特征模型的全系数自适应控制器的稳定性分析中起着关键的作用，有必要在更加一般的框架内分析两者的稳定性质.

根据文献［5］，当要实现位置保持或位置跟踪控制时，特征模型一般可用如下两种二阶时变差分方程形式描述：

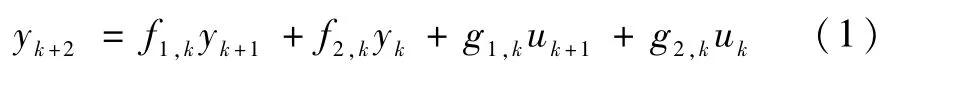
或

其中，f1，k，f2，k，g1，k，g2，k∈ R为特征参量.在具体的特征建模中，采用精确离散化的方法往往破坏了系统原有的严格反馈结构［6］，得到形为（1）的差分方程形式，而采用欧拉近似离散化则可以较好得保持系统的严格反馈结构，得到形为（2）的差分方程.由于特征模型在原系统的稳定性分析中仅起着过渡性的作用，基于式（1）或（2）进行特征模型闭环系统稳定性分析在原系统整个稳定性分析中的作用是等价的，因此，本文以式（2）为代表在更一般的框架下对单输入单输出系统和多输入多输出系统的黄金分割控制器的稳定性、鲁棒性进行系统分析，由于投影梯度法在特征建模方法中本质上是混合辨识，因此有必要在此背景下对其稳定性质进行研究.最后的结果进一步扩展了已有的结论，对于最终整个系统稳定性分析起着重要作用.

1 特征模型

由于本文并不研究特征建模问题，因此仅作如下假定：

设单输入单输出系统完全可控可观

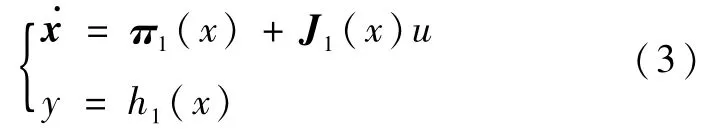
其中，x∈Rn，π1（x），J1（x），h1（x）均为光滑函数.假设在满足一定条件下采用欧拉近似离散化方法可化为如下特征模型：

特征参量属于如下闭凸集：

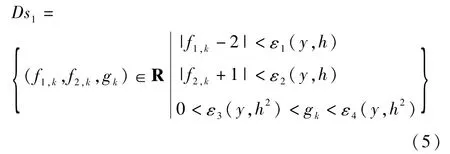
其中，采样周期0＜h＜1，εi为连续函数且分别为h、h2的同阶无穷小.

设多输入多输出系统完全可控可观

其中，x∈Rn，y，u∈Rm，π2（x），J2（x），h2（x）均为光滑函数.假设在满足一定条件下，采用欧拉近似离散化方法可化为如下特征模型：

特征参量属于如下闭凸集：

其中，0＜h＜1，εi为连续函数且分别为h、h2的同阶无穷小.

2 黄金分割反馈控制器

本节主要研究在特征模型（4）和（7）的基础上，黄金分割反馈控制器的鲁棒性.

2.1 单输入单输出系统

对于特征模型（4）的黄金分割反馈控制器一般可设计为：

其中，l1=0.382，l2=0.618，λ为设置参数，

下面将研究反馈控制律（9）在f1，k，f2，k，gk∈Ds1时的鲁棒性问题.因而，假设特征参数已知，把反馈控制器（9）代入特征模型（4），得到如下类型闭环系统：

yk+2=（1-l1kg）f1yk+1+（1-l2kg）f2yk（10）其中，f1=2+δ1（y，h），f2=-1-δ1（y，h），g∈Ds1，h2的同阶无穷小连续函数.

从Ds1形式可知，对于（10）平衡点附近的一个开子集Y1⊂R和h*＞0，当y∈Y1和h∈（0，h*）时系统（10）可以看作参数属于一个有界闭凸集Ds1的系统族，控制器的鲁棒性问题可以转换为保证该系统族中每个系统的稳定性问题.由于根轨迹具有明确直观的特点，因此，下面采用根轨迹的方法，首先分析标称系统的稳定性，并利用根轨迹的连续性分析受扰系统的稳定性.

对于由（10）表示的系统族内任意系统，其闭环特征方程可写为：

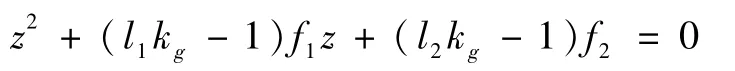
进一步变换成参数根轨迹形式可有

定理1.对于平衡点附近的开子集 Y1⊂ R，存在h*＞0，当y∈Y1和h∈（0，h*）时，存在λ使得闭环系统（10）为D（0，r）—稳定的.

证明.首先分析标称系统，然后利用连续性分析含有误差的系统的稳定性.

（1）当f1=2，f2=-1

由于特征参量f1在2附近变化，f2在-1附近变化，所以首先研究此种情况下的根轨迹，其他情况下的根轨迹均可看作此种情况下的摄动.当取l1= 0.382，l2=0.618时，该根轨迹如图1所示.其中A，B，C，D 4点对应的增益分别为kA=2.88，kB=1，kC=∞，kD=0，两个特征根分别分布在直线A-B和B-C或弧线B-D-B上.因此，B点对应闭环系统最小谱半径为0.618，且当kg∈［0，2.88］时标称系统特征根在单位圆内，当kg=1时谱半径最小，此时λ=0.

图1 标称闭环系统根轨迹Fig.1 Root locus of nom inal system

（2）当f1=2+δ1（y，h），f2=-1-δ1（y，h），

对于y∈Y1和h＞0，此时的根轨迹可以看作图1的根轨迹受到f1，f2偏离2，-1的扰动而生成的.因此，假设当f1=2，f2=-1，存在k*g使得特征穷小连续函数δ1（y，h）∈R，当f1=2+δ1（y，h）和f2=-1-δ1（y，h）时，可以构建如下辅助方程：根据根轨迹的连续性及连续函数δ1（y，h）对于h的同阶无穷小特性，对于每个固定的 k*

g，存在 h*使得新系统的特征根满足例如当k*g=0.7时，在图 2中分别画出对应于δ1（y，h）＞0和 δ1（y，h） ＜0的根轨迹，从图中可见，点 O1和 O2对应没有扰动的特征根，即对应δ1（y，h）=0.A点对应δ1（y，h）=-2.32时的一个特征根，B点对应δ1（y，h）=0.62时的一个特征根.因此，当δ1（y，h）在0附近变化时，相应的特征根也在O1和O2附近沿着图2所示的根轨迹变化，即对于任意y∈Y1，当选择一个kg≠0（对应λ=使得当f1=2，f2=-1时的标称系统的特征根h*，使得h∈（0，h*）时保证δ1（y，h）足够小，导致受扰系统（即f1=2+δ1（y，h），f2=-1-δ1（y，h））也是稳定的.例如，当取k*g=0.7时，我们可以说系统的根轨迹具有的稳定裕度为［-2.32，0.62］，即对于任意y∈Y1，存在h*使得当h∈（0，h*）时，δ1（y，h）∈ ［-2.32，0.62］，因此受扰系统在此控制器下仍然是稳定的.

图2 受扰系统根轨迹Fig.2 Root locus of disturbed system

同理可有，此类情况下的根轨迹可看作图1根轨迹由误差δ2（y，h2）导致的摄动.具有与上述情况类似的结论.

总结（1）～（3）可有：对于任意y∈ Y1，假设当得闭环系统的特征根满足据根轨迹的连续性和连续函数 δ1（y，h），δ2（y，h2）对于h和h2的同阶无穷小特性，存在一个 h*使得对于每个 h∈（0，h*），当 f1=2+δ1（y，h），f2=0使得系统（10）特征根满足ε＜1））.证毕.

注1.从以上分析可以看出，黄金分割反馈控制器具有一定的鲁棒性，而且我们可以通过减小采样周期从而减小特征参量的摄动空间δ使得该控制器可以稳定更大的扰动.并从图1根轨迹看出，使得系统稳定的kg是有界的且在1附近取值.

2.2 多输入多输出系统

对于特征模型（7）的黄金分割反馈控制器一般可设计为：

其中，

λij为设置参数保证Kg非奇异数，yr为参考输入.

进一步推广上面的结论，利用特征值对于矩阵元素的连续性研究MIMO反馈控制器（11）的鲁棒性.把反馈控制器（11）代入特征模型（7）得到如下类型闭环系统：

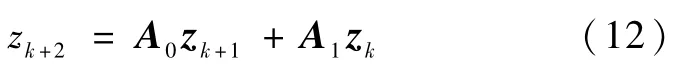
定理2.对于平衡点附近的开子集 Y2⊂ Rm，存在h*＞0，当y∈Y2和h∈（0，h*）时，存在λij，i，j= 1，…，m使得闭环系统（12）为D（0，r）—稳定的.

证明.首先分析标称系统，然后分析含有误差的系统的鲁棒性.D（0，r）稳定的.为了简化分析，仅证明Kg存在性.首先假设Kg=diag{k1，g，…，km，g}，则系统变为m个完全独立的子系统：

其中，i=1，…，m，fi1，k=2，fi2，k=-1.把ki，g看作未知增益，根据定理1利用根轨迹可以证明系统为D（0，r）稳定的，且当 ki，g=1时最小谱半径为0.618.对（12）当 Kg=I时，状态矩阵可定义为A*k，此时ρ（A*k）=0.618.当Kg不为对角阵时，由特征值对矩阵元素的连续性可知，耦合系统的特征值在A*k特征值附近摄动，摄动范围由Kg相对于I的距离决定，当 Kg与 I的差异很小时 ρ（Ak）≤0.618+Δ，（0≤Δ≤1）.

（2）当F1=2I+δ2（y，h），F2=-I-δ2（y，h），

对于y∈Y2和h＞0，同样根据文献［7］中的区域稳定定理3.1.2，当以下条件成立时系统也是D（0，r）稳定的，

（1）当F1=2I，F2=-I，

根据文献［7］中的区域稳定定理 3.1.2，当

其中，ΔA0=

由于减小采样周期导致δ1（y，h2），δ2（y，h）同时变小，所以，必存在h*＞0，当h∈（0，h*）时以上条件成立.最后，由Kg形式可知当Kg一定，并由有界性可知存在对应的λij，i，j=1，…，m，则根据（1）～（2）可知，定理得证.

例1.对于n=2的系统，当取固定的δ1=［0.0045 0.0001；0.0001 0.0050］，δ2=［0.03 0.03；0.03 0.03］时，可取Kg=［0.9 0.01；0.02 1］使得闭环系统特征值为 λ=0.6626±0.1133i，0.5932，0.6605.

注2.根据Kg的具体形式可以看出，由于Gk有界，可以选择λij减小系统间的耦合程度，保证系统稳定.而当减小采样周期时可以保证标称系统可以稳定更大的扰动.以上定理仅证明其存在性和保证系统稳定性时Kg的大致范围，而并没有给出具体的取值，如果给定具体的A0A1，要计算λij一种方法是可以通过线性矩阵不等式（LMI）或直接根据文献［7］中的区域稳定定理3.1.2寻求一个最优解得到.

3 投影梯度法自适应律

3.1 自适应律

基于特征模型的自适应控制一般采用相应的特征模型结构作为辨识模型，对于单输入单输出系统和多输入多输出系统的每个输出子系统均有

其中，Φ（k）分别对应（4）或（7）子系统特征模型的特征变量，θ（k）、k）为其对应的特征参量的真实值和估计值.

由于通过特征建模把原来复杂的动力学模型构建为与其等价的线性形式，因此特征模型的参数一般是未知且随状态变化并且在一个已知的闭凸集内，一般采用投影梯度法辨识得到，对每个输出子系统，自适应律一般可取为

为了保证辨识参数指数化收敛，引入如下充分激励假设：

假设1.Φ满足PE条件.

3.2 自适应律性质

由于在特征建模框架下，被控系统一般为连续系统，而辨识模型为离散系统，因此辨识问题属于混合辨识的范畴.而在采样系统中，根据文献［8-9］提出的基于欧拉近似离散模型的采样系统稳定性分析方法，对于向量场满足局部Lipstchiz的非线性对象=f（x，u）和采样控制器uk=uh（xk），考虑系统的精确离散时间模型

和欧拉近似模型

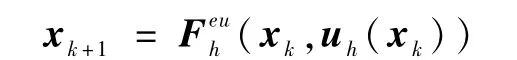
对于任意紧集X1⊂Rn，都存在常数0，当h∈（0，h*1）时，对于任意x∈X1存在如下关系：

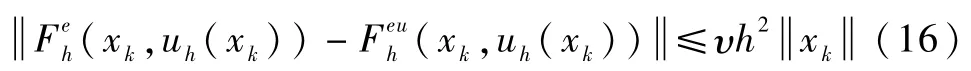
因此，对于下面混合辨识的分析，可以以此为基础展开.首先分析离散辨识问题，然后以（16）作为过渡分析混合辨识问题.由于特征建模把原来的非线性系统化为一种伪线性变参数形式，导致特征模型本质上是线性变参数的，并可以构建一个依赖于状态变量和采样周期的闭凸集（如式（5）（8）中的Ds1和Ds2，此处统称为Ds），特征参量及其变化率的上界可以通过减小采样周期而减小，从而导致特征模型为慢变系统.因此，辨识问题可以归入有界慢变自适应理论框架中进行分析.所以假设特征模型为实际系统时，辨识环节具有以下特性.

引理1.在PE假设下，自适应律（15）在未知参数慢变并属于闭凸集Ds和待辨识系统受到外部扰动pk的情况下具有如下性质：

其中c1，c2，ϖ为正常数，ε为连续函数且为 h的同

阶无穷小.

证明.对性质1），自适应律（15）两边减去θk可得

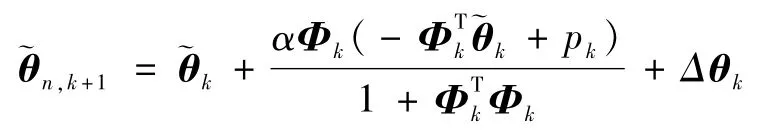
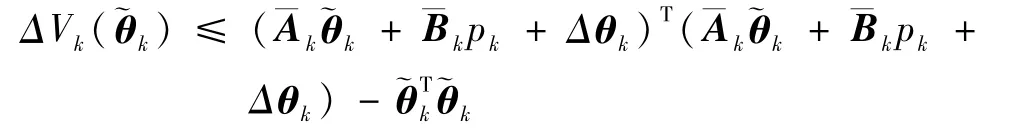
整理可得

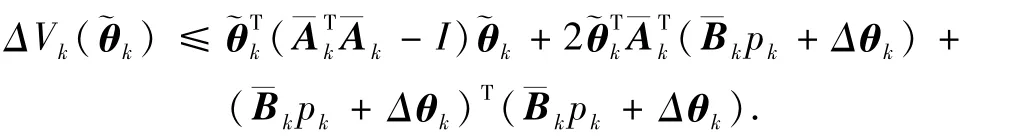
由于在没有外部扰动时，自适应律（15）在 PE条件下为指数稳定的，即对于并利用可得

存在常数c，满足r-2c2＞0，使得

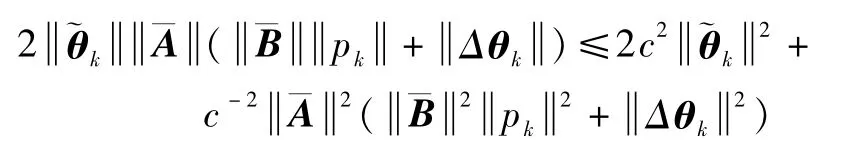
所以有

因此，根据离散系统 ISS性质（见文献［10］），存在χ∈K∞和γ∈K使得所以自适应律关于 pk，Δθk是 ISS的.对于 ˆθ可写为

对性质2），对式（18）从k=0到N求和并移项可得

注3.性质1）表明，如果自适应律的外部扰动为0，则辨识过程是稳定的，而由于特征参量为系统状态变量的函数，因此当系统状态稳定且不存在外部扰动时，特征参量及其估计值也收敛到一个恒定值；性质2）给出了特征参量辨识误差的一个 L2界，该界有助于最终时变系统的稳定性分析.

以上引理只是分析了自适应律对于实际系统为特征模型时参数辨识具有的性质，由于实际系统为连续系统而辨识模型为离散形式，并且特征模型及特征参量所属闭凸集均基于欧拉近似离散化得到，因此连续系统的实际输出并不等同于辨识模型的输出，之间的差异可视为对自适应律的时变扰动，因此总结起来这种混合辨识系统在受到外部扰动 p（t）时自适应律（15）存在如下时变扰动：

1）参数时变扰动：由于特征参量依赖于状态变量，因此特征参数是时变的即存在的扰动

2）近似离散化误差扰动：根据采样系统基于欧拉近似离散化稳定性分析框架，由于在欧拉近似后，根据式（16）系统存在一个近似离散导致的时变误

3）外部扰动p（t）.

因此在引理1的基础上有如下定理.

定理3.对于单输入单输出系统（3）或多输入多输出系统（6）的每个输出子系统，采用 （4）或（7）为辨识模型，辨识参数属于闭凸集（5）或（8），自适应律（15）在PE假设和系统受到外部扰动p（t）的情况下具有如下性质：

其中c1，c2，c3，ϖ为正常数连续函数且为h的同阶无穷小.

证明.由于多输入多输出系统（6）当输入输出通道数为1时退化为单输入单输出系统（3），因此以（6）的每个输出子系统为单位进行分析具有代表性.假设（6）的精确离散化解为的输出为欧拉离散化后的解为对应的输出为 yeu=根据式（16），对于任意紧集X1⊂ Rn其精确解与离散化后的欧拉近似解存在如下关为输出有

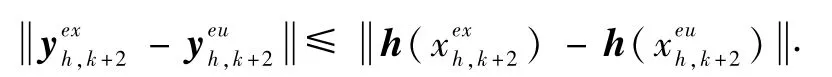
根据局部Lipstchiz性质，存在lx＞0，使得

又根据文献［11］定理 A.1，由于系统可控可观，则在X1内存在光滑函数Θ，使得x=Θ（y，u），并由其局部Lipstchiz性可得其中ly，u＞0，所以最终有

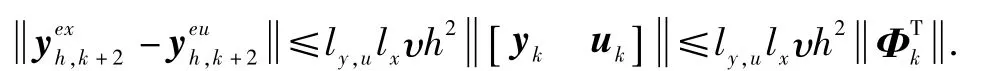
根据引理1可知性质1）成立，并有：

证毕.

注4.相对于引理1的性质2），混合系统辨识过程多出一项c3h4（N+1），可以看作是由于近似离散化误差导致的扰动，由于此项为采样周期的高阶项，因此当减小采样周期时此项为一个极小量.

综合引理1与定理3可知，在特征模型框架下的混合自适应律相比一般的定常系统受到一些时变扰动，而由于投影到一个闭凸集中保证了参数估计误差的L2有界性，该性质对于最终系统稳定性分析有重要作用.

4 结 论

本文在更加一般的条件下讨论了黄金分割控制器的鲁棒性和投影梯度法在特征模型框架下具有的一些性质，这些性质对于系统稳定性分析起着重要作用，然而不足之处在于对于黄金分割控制器只是证明了存在配置参数λ保证系统 D（0，r）稳定的，但是对于在时变条件下，特别是对于多输入多输出系统如何求取 λ使得系统的特征值在要求的范围内将是下一步的工作.

［1］ Xie Y C，Wu H X.The application of the golden section in adaptive robust controller design［J］.Acta Automatica Sinica，1992，18（2）：177-185

［2］ 解永春.航天器鲁棒自适应控制方法及其应用研究［D］.北京：中国空间技术研究院北京控制工程研究所，1994 Xie Y C.Study on robust adaptive control method and application of Spacecraft［D］.Beijing：Beijing Institute of Control Engineering，China Academy of Space Technology，1994

［3］ 齐春子.TDRS多变量自适应控制方法研究［D］.北京：中国空间技术研究院北京控制工程研究所，1999 Qi C Z.Study on TDRSmulti-variable adaptive control method［D］.Beijing：Beijing Institute of Control Engineering of Control Engineering，China Academy of Space Technology，1999

［4］ 孙多青，吴宏鑫.四阶时变离散系统的一致渐进稳定性［J］.控制理论与应用，2006，23（6）：845-852 Sun D Q，Wu H X.Uniform ly asymptotic stability of the 4th-order time-varying discrete systems［J］.Control Theory&Application，2006，23（6）：845-852

［5］ 吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制［M］.北京：中国科学技术出版社，2009 Wu H X，Hu J，Xie Y C.Characteristic model-based intelligent adaptive control［M］.Beijing：China Science and Technology Press，2009

［7］ 周武能，苏宏业.区域稳定性约束鲁棒控制理论及应用［M］.北京：科学出版社，2009：47-48 Zhou W N，Su H Y.Reginal stability constraints of robust control theory and application［M］.Beijing：Science Press，2009，47-48

［8］ 金辉宇.基于近似模型的非线性采样系统研究［D］.合肥：中国科学技术大学，2007 Jin H Y.Study on nonlinear sampled-data system based on approximated model［D］.Hefei：University of Science and Technology of China，2007

［9］ 金辉宇，康宇，殷保群.局部Lipstchiz系统的采样控制［C］.第29届中国控制会议，北京，2010 Jin H Y，Kang N，Yin B Q.Sampled-data Control of locally lipschitz system［C］.The 29thChinese Control Conference，Beijing China，2010

［10］ Jiang Z P，Wang Y.Input-to-state stability for discretetime nonlinear systems［J］.Automatica，2001，37（6）：857-869

［11］ Sadegh N.Minimal realization of nonlinear systems described by input-output difference equations［J］.IEEE Transactions on Automatic Control，2001，46（5）：698-710

Analysis for Several Stability Properties of A ll-Coefficient Adaptive Controller

WANG Yong1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.Science and Technology on Space Intelligent Laboratory，Beijing 100190，China）

Undermore general conditions，the stability and the robustness of golden-section feedback control law are analyzed in this paper，and in the framework of hybrid identification，the input-state stable（ISS）property of the gradient projectmethod used in SISO and MIMO characteristic models is studied，and the L2bound of estimated errors of characteristic parameters is obtained.The final results further generalize the former results and play very important roles in the stability analysis of entire hybrid system.

all-coefficient adaptive controller；characteristic model；golden section；gradient project method

TP13

A

1674-1579（2012）02-0010-07

王 勇（1978—），男，博士研究生，研究方向为航天器智能自适应控制.

*国家自然科学基金资助项目（60736023，60704014）.

2011-07-04

DO I：10.3969/j.issn.1674-1579.2012.02.003