一种高性能控制力矩陀螺框架控制方法的仿真研究

张 雪，魏大忠，周大宁

（北京控制工程研究所，北京 100190）

一种高性能控制力矩陀螺框架控制方法的仿真研究

张 雪，魏大忠，周大宁

（北京控制工程研究所，北京 100190）

由控制力矩陀螺群构成的姿态控制系统是目前敏捷卫星实现姿态快速机动和精确控制的最佳选择，而低速框架的控制精度、响应速度与稳定性直接决定了控制力矩陀螺的工作性能.针对敏捷卫星对控制力矩陀螺工作性能的高要求，本文提出了一种框架的高性能控制方案——基于永磁同步电机及磁场定向控制算法，并结合框架角速度观测器的直接驱动控制方案.在框架角速度极低时，为解决角度传感器的分辨率无法满足控制精度要求的问题，引入Luenberger状态观测器获得框架角速度的观测值，并将该观测值引入框架角速度闭环控制系统.理论分析、仿真实验的结果证明了该方案的有效性.随后，针对电机参数漂移对观测值的影响进行了仿真分析，仿真结果证明了基于观测器的角速度闭环控制系统的鲁棒性.

控制力矩陀螺；框架；永磁同步电机；观测器

目前，控制力矩陀螺构型系统是实现敏捷卫星 姿态快速机动和高精度控制的最佳方案.为实现控制力矩陀螺高精度快速输出力矩的目标，应对框架系统进行高性能驱动控制.

控制力矩陀螺的研制中，常用的框架驱动方案包括间接驱动方案和直接驱动方案两种.比较而言，直接驱动方案的框架控制系统实现难度较大，但其框架控制带宽较高，且由于取消了减速器，整机重量得到降低，而机械组件的可靠性得到提高.

为实现较高的控制带宽和角速度控制精度，采用基于永磁同步电机和矢量控制算法的框架直接驱动方案，并通过角度传感器获取角度测量信息.实际应用中，控制力矩陀螺的框架最低角速度达到0.001（。）/s.当角速度极低时，若通过角度传感器获取框架角速度信息，则在一个控制系统采样周期中，采集到的角速度值离散程度较大，与实际值之间的相对误差也较大，这将降低角速度控制精度与闭环控制系统稳定性.

框架角速率极低时，为获得准确的角速度值，以提高闭环系统的稳定性和控制精度，采用状态观测器获取角速度信息.

目前已得到充分研究的无速度传感器的方法有卡尔曼滤波法［1］，Luenberger观测器［2］，模型参考自适应方法［3］，基于神经网络的自适应［4］等方法.基于模型的收敛性、稳定性及计算量等的分析的基础上，本文基于Lyapunov稳定性理论，设计了电机运行状态的Luenberger观测器，在框架角速度极低时获取角速度观测值，并将该角速度观测值引入框架闭环控制系统.仿真结果验证了提出的方案的有效性.

1 CMG框架控制

1.1 框架矢量控制方案

采用永磁同步电机对CMG框架组件进行直接驱动控制，对该电机进行基于转子磁场定向的矢量控制，达到对定子电流中的励磁分量和力矩分量进行解耦闭环控制的目的.

在电机的电角度空间，d-q正交坐标系的d轴固定在转子永磁体磁链方向上，d轴正方向与N极重合.则d-q坐标系下电机的动态数学模型是：

式中，J——电机负载转动惯量；

Tf——框架摩擦力矩；

pn——电机极对数.

1.2 框架控制系统

在框架角速度变化范围内，角速率越高，则由角度测量单元得到的角速度值的相对误差越小，框架控制系统的稳定性越高.角速率极低时，考虑到角度测量单元有限的分辨率，测得的角速度相对误差较大.

考虑到分辨率高且符合空间环境要求的角度传感器难以获得，以及机械安装方法和力学环境对高精度角度传感器的精度的影响等问题，本文在角速度极低的工况条件下采用角速度观测器，并将角速度观测值引入闭环控制系统.而在角速率相对较高时，为减小控制器的计算量，仍采用角速度测量值实现闭环控制.

本文设计的框架闭环控制系统结构如图1所示，图中REG1、REG2、REG3分别为励磁电流调节器、力矩电流调节器和角速度调节器，SVPWM为空间矢量脉冲宽度调节算法，MUX为多路复用器，PMSM为永磁同步电机.

1.3 角速度观测器

图1中，ω*为额定角速度，若角速度指令值幅度大于某个域值ωmth，则可直接将角度传感器输出的测量值引入闭环控制.否则，通过观测器计算出角速度观测值，并将该观测值作为反馈量引入闭环控制.

式中，Rs2=1.5Rs；

Ld=Lq=1.5（LS-LM）；

ψf2=1.5ψf；

vd、vq——电机d、q轴电压；

id、iq——电机d、q轴电流；

Rs——电机定子绕组等效电阻；

Rs2——d、q轴绕组等效电阻；

Ld，Lq——d、q轴电感；

LS——定子绕组等效电感；

LM——任意两定子绕组间的等效互感；

ωe，ωm——转子电角度，机械角度；

ψf——电机转子永磁体磁链幅值；

ψf2——两相转子坐标系下永磁体等效磁链幅值.

电机在相同坐标系下的机械方程：

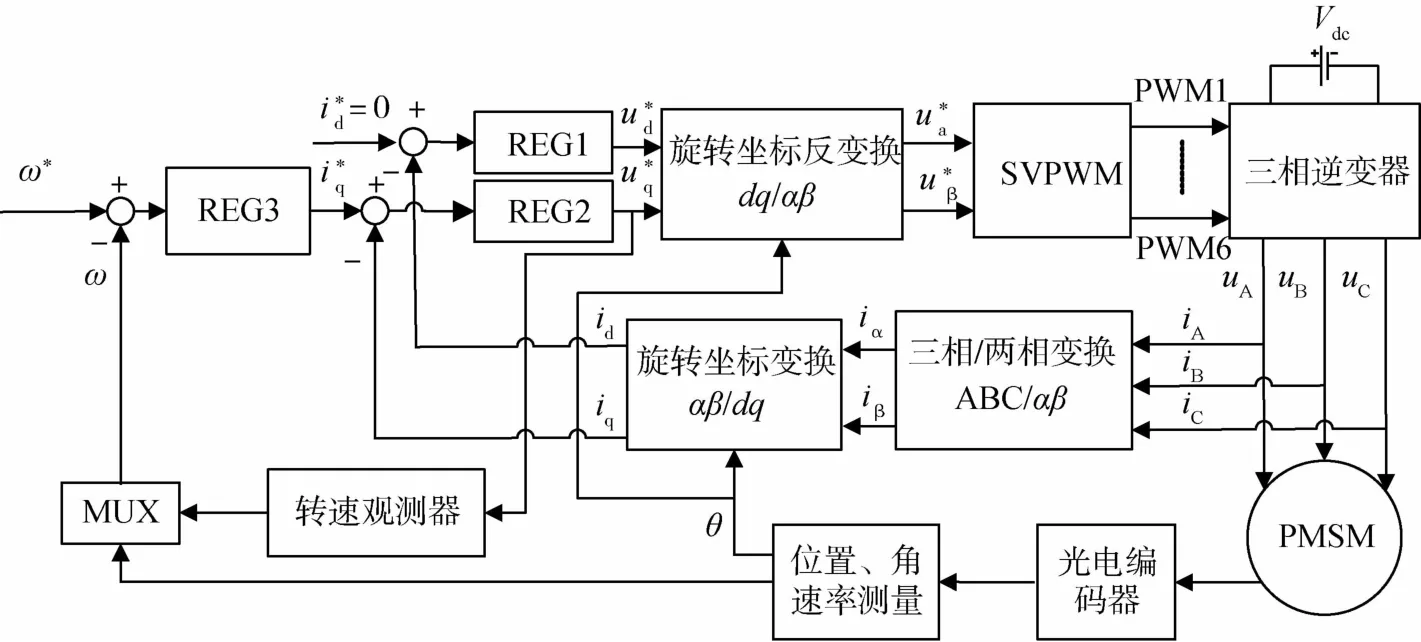
图1 框架控制结构框图Fig.1 Gimbal control structure block diagram

考虑到采用了id=0的矢量控制方案，闭环系统稳定工作时，式（1）可忽略id的影响，得

由式（2），得

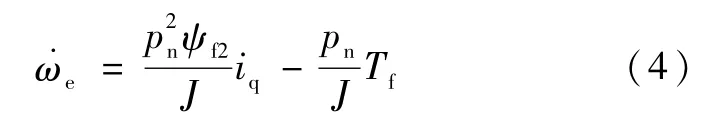
式（3）、（4）可写成

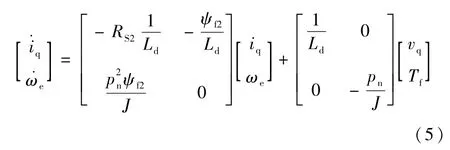
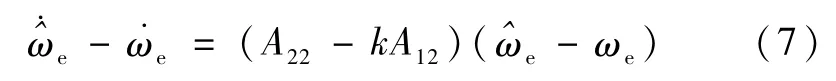
则有：

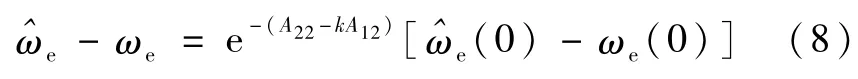
由式（5）和（8）可知，在 k取负值的情况下，式（8）中-ωe将渐近衰减至零，即角速度观测值渐近地逼近实际角速度值，且 k的绝对值越大，收敛至ωe的速度越快.

但若k值过大，考虑到实际电机参数与其辨识值之间的误差，相关电流、电压量的测量误差的存在，闭环控制系统稳定性将降低.实际控制系统设计中，可根据电机电气时间常数等参数，合理设计 k值，使的收敛速度满足闭环控制的需要.

由式（7），得：

式（5）表示成如下形式：将式（6）第二行代入式（9），得：即：

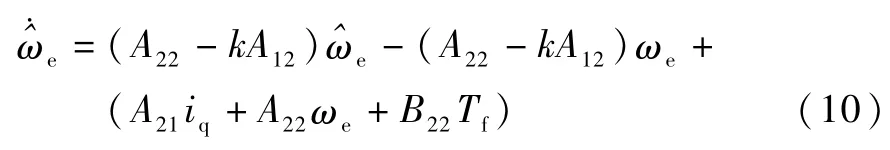
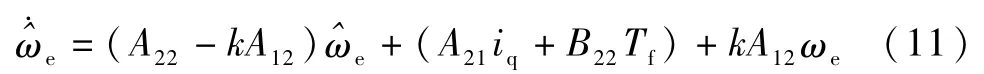
由式（6）第一行，知：

将式（12）代入式（11），得：

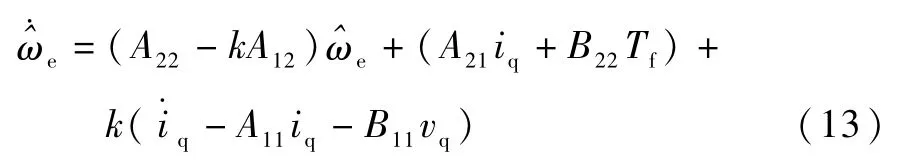
令：

将式（14）代入式（13），得：

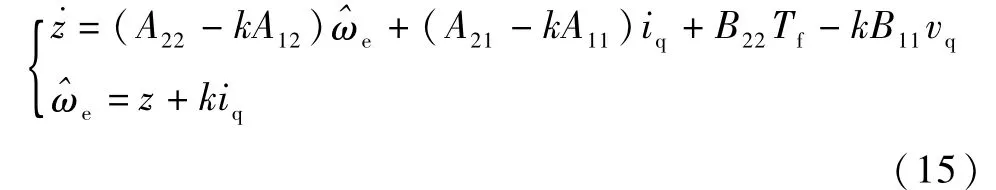
式（15）给出了角速度观测值收敛速度由系数k决定的Luenberger观测器.

在角速率极低的工况下，框架组件的摩擦力矩呈现出很强的非线性特点，对角速度闭环控制系统的稳定性、精度、响应速度等有很大影响.

根据式（4），可得到摩擦力矩Tf的计算方法：

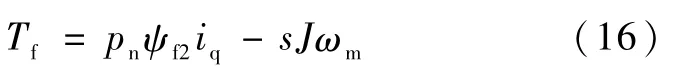
由式（16）知，Tf的计算涉及到角速度值的微分运算，为降低微分运算对闭环系统稳定性的不利影响，可在计算出的Tf值反馈到角速度观测输入端的通道中加入低通滤波器既可抑制角速度微分计算引入的噪声，也可衰减电流iq中的高频谐波成分.

完整的框架角速度观测器如图2所示.

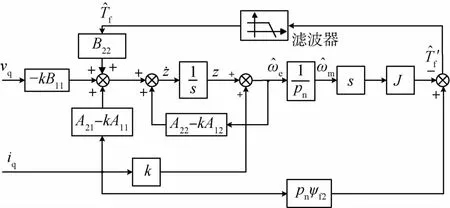
图2 观测器结构图Fig.2 Observer structure block diagram

低通滤波器中，系数a的值越小，则滤波器转折频率越低，带宽越小.选择a值的标准是，抑制摩擦力矩观测值中的高频噪声，使框架控制系统既具有较好的稳定性能，也满足动态性能的要求.

另一方面，考虑到在角速度阶跃且角速度已进入稳定状态的条件下，以及在角速度跟随其指令值作缓慢变化的条件下，式（16）中的sJωm项的幅值相比于pnψf2iq的幅值小得多，则可研究忽略sJωm项，计算出观测值，并将和作为反馈量引入闭环控制的效果.

2 基于观测器的框架控制系统仿真

为全面评估框架控制方案的工作性能，建立了较为完整的框架控制系统仿真模型.通过该仿真模型，可研究框架控制系统中各调节器结构和参数、摩擦力矩、电机参数等变化对系统工作特性的影响.

2.1 不存在摩擦力矩影响时闭环控制系统的响应

仿真时首先忽略测量噪声，将真实的角速度值反馈到闭环系统中，调节PID参数可使系统的收敛时间达到约0.001s.然后，采用观测器对角速度进行观测，将观测到的反馈到闭环系统，k取为-15，框架角速度指令设置为1（。）/s时，角速度观测值的收敛时间约为0.002s.仿真结果如图3所示.由式（9）知，pnψf2iq基本恒定，且角速度进入稳态后sJωm项的值非常小，约为pnψf2iq的0.1%，因此可忽略sJωm项.

图3 k=-15时角速度观测值Fig.3 Observated angular rate value for k=-15

忽略Tf影响，分别采用21位的角度传感器和Luenberger观测器，将其输出分辨引入闭环系统的反馈输入端.仿真中的框架角速度指令设为0.001（。）/s.仿真结果图4所示.

图4 额定角速度0.001（。）/sFig.4 Rated angular rate is 0.001（。）/s

通过仿真可看出角速度达到稳态后，采用观测器时角速度的波动量约为1%，而使用角度传感器时的波动量达40%；0.5s内采用观测器框架的机械角度基本接近额定值，采用角度传感器框架的机械角度值误差为10%.频域上来看，这是由于角度传感器采集到的角速度值中含有丰富的控制器频率成分（4kHz）及其倍频成分，而角速度控制系统的闭环带宽不大于120Hz，因此，作为被控制对象的角速度中的较高的频率成分无法通过闭环控制系统得到衰减.

2.2 存在摩擦力矩时闭环控制系统的响应

在框架角速率很低时，摩擦力矩对于控制系统的稳定性、角速度控制精度、动态响应能力等均有较大的影响.经典的摩擦模型包括：Dahl模型［5］、库仑模型、黏性模型、Stribeck模型［6］和静摩擦模型［7］等.考虑到模型与实际情况应尽可能接近这一原则，本文根据经验数据，建立了摩擦力矩模型加入仿真模型中进行仿真研究，并在摩擦力矩模型中加入了白噪声.

仿真工作中，采用了图5所示的摩擦力矩模型.其特点是：角速率小于0.001（。）/s时，将其看作小位移时的静摩擦力矩，并将0.001（。）/s看作静、动摩擦之间的分界点，该分界点对应的摩擦力矩值为0.1N·m；角速度高于0.001（。）/s后，将其看作进入滑动摩擦状态；当角速度继续上升至大于5（。）/s，则摩擦力矩与角速度呈线性关系变化.该模型在转角变化范围较小时，与实验数据的变化趋势大体吻合.

框架角速度指令设为1（。）/s，取a=100时，滤波器的转折频率点为100Hz，带宽为15Hz，仿真图形如图6中（a）所示；（b）为不将送入角速度观测器的仿真结果；（c）为框架转过的角度值.

图5 摩擦力矩模型Fig.5 Frictional torque model

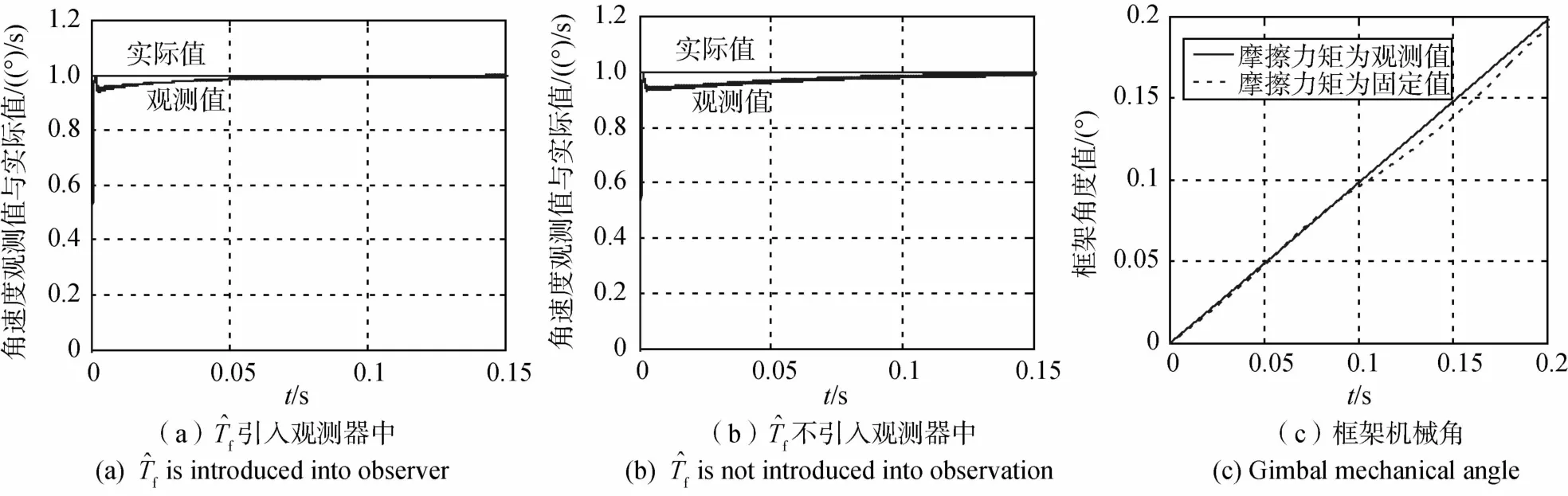
图6 额定角速度1（。）/sFig.6 Rated angular rate is 1（。）/s

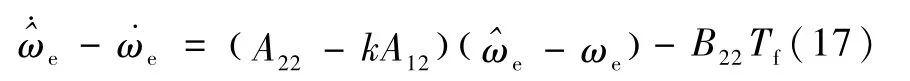
若暂时只考虑B22Tf中的常量，则有：

式中C为由初始状态确定的某个常数.

时间T内，转子转过的角度误差可由式（19）求得：

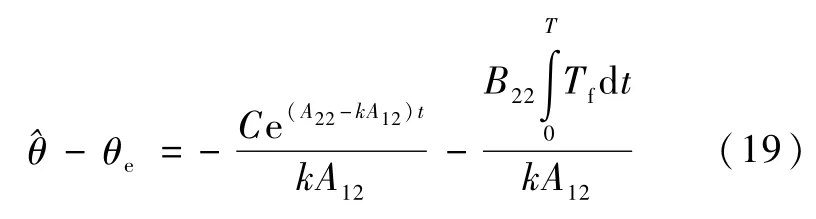
摩擦力矩观测的仿真结果如图7所示.

图7 摩擦力矩观测值与实际值Fig.7 Observed value and actual value of frictional torque

图7 中摩擦力矩的观测值可在约0.06s后接近实际值，且观测值与实际值相似.

2.3 系统带宽及参数漂移对系统的影响

在存在摩擦力矩的情况下，向闭环控制系统发出如图8所示的正弦转速指令，仿真结果也在图8中给出.

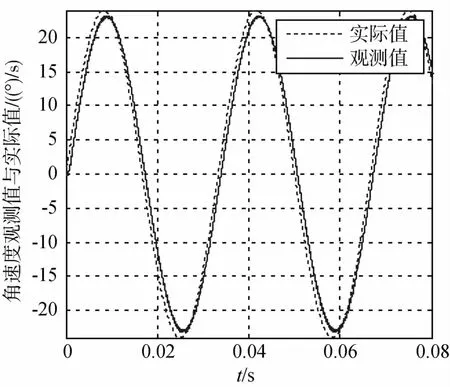
图8 输入为正弦信号时角速度值Fig.8 Angular rate value when input is sinusoidal signal

由图8可看出，正弦角速度指令频率为30Hz时，实际转速幅值衰减为0.4dB，这说明了其响应带宽可达到30Hz.

在实际的工程应用中，电机定子电阻、电感以及转子磁通都会随着使用环境、温度、电流、频率等因素发生一些变化.尤其是定子电阻，除受环境温度影响外，还受定子电流的影响.为了检验在电机参数发生变化时，提出的控制方案是否有效，并验证参数变化时是否具有较高的角速度控制精度及稳定性，在框架系统模型的基础上对参数可能出现的变化做进一步仿真.

根据经验估计，无故障情况下电机参数 R、L、 ψf2变化幅度不超过20%，在不同的额定角速度下，对这3个参数分别漂移以及R和L同时变化时进行仿真.参数的变化幅度采用可能发生的最坏情况即幅值变化20%.

取k值为-15，a为100，角速度为1（。）/s时的仿真结果对比如表1所示.

表1 角速度为1（。）/s时仿真结果Tab.1 Simulation result when rated speed is 1（。）/s

表1的对比中，定子电阻变化对控制精度和收敛时间的影响较电感的变化明显，两者同时变化时角速度控制精度主要受定子电阻的影响.随着永磁体材料的不断改进，转子磁通受温度的影响很小，基本保持恒定，转子磁通的变化幅度很难达到20%，对观测值的影响较小.

因此电机参数发生漂移时采用图2的观测器结构仍可以较为准确的观测出角速度.比起采用角速度传感器（1（。）/s时稳态误差约为2.5%），具有更好的角速度控制精度.

3 结 论

针对角度传感器很难满足框架高精度控制要求的问题，设计了框架角速度Luenberger观测器，并建立了框架闭环控制系统的完整数学模型.

通过仿真分析，验证了角速度极低时采用观测器获取角速度观测值的可行性，理论上可获得令人满意的角速度控制精度.在角速度观测器中加入摩擦力矩观测值的影响，可提高系统的控制精度和响应速度.使用角速度观测器时，理想情况下闭环控制系统的带宽可达30Hz.最后验证了电机电气参数发生漂移时闭环控制系统的控制性能.

实际工作中除摩擦力矩外，控制力矩陀螺框架控制的性能还将受到高速转子高频扰动力矩，星体低频耦合力矩等的影响.在实际运动条件下的框架控制系统的性能，及极低速情况下应用角速度观测器的可行性等课题，是下一步研究的重点.

［1］ Albert Q，Bin W，Sensorless control of permanentmagnet synchronous motor using extended Kalman filter［C］.Canadian Conference on Electrical and Computer Engineering，Niagara Falls，Canada，2004

［2］ 张激扬，周大宁，高亚楠.控制力矩陀螺框架控制方法及框架转速测量方法［J］.空间控制技术与应用，2008，34（2）：23-28 Zhang J Y，Zhou D N，Gao Y N.Gimbal control technique and gimbal rate measurementmethod for the controlmoment gyro［J］.Aerospace Control and Application，2008，34（2）：23-28

［3］ Zhi Q C，Tomita M I.Sensorless control of interior Permanent magnet synchronous motor by estimation of an extended electromotive force［C］.IEEE Industry Applications Conference，Rome，Italy，2000

［4］ 武宏伟，戴琼海，王普.基于神经网络的非线性系统的观测器设计［J］.清华大学学报，2000，40（3）：44-47 Wu HW，Dai Q H，Wang P.Neural-network-based observers for nonlinear systems［J］.J Tsinghua Univ，2000，40（3）：44-47

［5］ John B S.Reaction wheel low-speed compensation using a dither signal［J］.Journal of Guidance Control and Dynam ics，1993，16（4）：617-622

［6］ Brian A H.Stick slip and control in low-speed motion［J］.IEEE Trans.on Automatic Control，1993，38（10）：1483-1496

［7］ Armstrong B.Control of machines with friction［M］. Boston：Kluwer Academ ic Publishers，1991，24-26

Sim u lation Study on a H igh Per form ance G im bal Control M ethod for Control M om entum Gyro

ZHANG Xue，WEIDazhong，ZHOU Daning
（Beijing Institute of Control Engineering，Beijing 100190，China）

The attitude control system constructed by a cluster of controlmomentum gyro（CMG）is the best choice tomeet the rapid attitude maneuvering and accurate control requirements of today’s agile satellites.Meanwhile，the control accuracy，response speed as well as stability of the gimbal control assembly determine the CMG performance directly.Focusing on the high performance requirement for agile satellites，a high performance gimbal controlmethod is proposed，by employing the permanentmagnetic synchronous motor（PMSM）with the field oriented control（FOC）algorithm，and utilizing a gimbal rate observer to drive the gimbalmechanical assembly directly in this paper.In order to solve the problem that the resolving rate of normal angular sensors are difficult to meet the accuracy requirement，a Luenberg state observer is introduced to obtain the observed gimbal rate value in the extremely low rate condition. The observed value is introduced into the closed loop system of gimbal rate thereby.Theoretical analysis and simulation experiments have proved the validity of the proposed method.Then，a simulation work is done to aim at studying the effect of motor parameter drifting on the observed value.The simulation results have demonstrated the robust performance of the proposed observer based closed-loop rate control system.

controlmoment gyro；gimbal；PMSM；observer

V44

A

1674-1579（2012）02-0035-06

张 雪（1986—），女，硕士研究生，研究方向为航天器执行机构；魏大忠（1977—），男，高级工程师，研究方向为航天器执行机构，高可靠空间精密机构；周大宁（1977—），男，高级工程师，研究方向为电力电子、自动控制等.

2011-10-03

DO I：10.3969/j.issn.1674-1579.2012.02.007