月球软着陆的高精度自主导航与控制方法研究

黄翔宇，张洪华，王大轶，李 骥，关轶峰，王鹏基

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

月球软着陆的高精度自主导航与控制方法研究

黄翔宇1，2，张洪华1，2，王大轶1，2，李 骥1，2，关轶峰1，2，王鹏基1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

提出了一种月球软着陆的高精度自主导航和控制方法.根据测距波束视线相对月面的几何关系，确定本体系的月心方向，组合利用测速仪获取的本体系三维速度确定本体系相对轨道系的姿态、速度及高度，并根据确定的参数性质选取适应的制导和控制方法.算法基于直接测量数据确定和控制姿态、高度和速度，不受惯性导航误差的影响，可以有效地提高姿态、速度与高度的确定精度和控制精度.数学仿真表明了算法的有效性.

月球软着陆；自主导航；制导与控制

在月球软着陆过程中，为了实时连续提供探测器的位置、速度和姿态信息，惯性导航成为基本的导航手段.为了保证软着陆导航精度，需要利用探测器相对月面的距离和速度测量信息修正惯性导航.因此，惯性导航配以测距测速修正成为月球软着陆的主要导航方式.对于月球软着陆探测器的导航，探测器相对着陆目标天体表面的距离和速度是重要的观测量，前苏联的Lunar系列、美国的Surveyor和Apollo系列探测器都采用测距测速仪获取探测器相对月面的距离和速度信息.目前导航一般采用的方法是利用惯性导航位置确定月心的方向，将测距仪获取的探测器相对月面的距离利用惯性姿态转化为相对月面的高度，结合测速仪获取的速度，以修正或替换惯性导航的高度和三维速度信息；但该方法无法修正惯性导航提供的月心方向和姿态误差，必然导致导航姿态、高度和速度误差随着时间的增大而逐渐增大，因此，无法满足高精度软着陆制导与控制的需求.针对此问题，本文提出一种月球软着陆的高精度自主导航与控制方法.

1 月球软着陆过程

为了完成软着陆任务，着陆器需要从环绕轨道经霍曼转移到达近月点，经过复杂的轨道机动，在一定的误差范围内，在预定的月球表面着陆点附近软着陆.如图1所示，月球软着陆过程一般可分为5个阶段［1］.

1）主减速段.从近月点到距月面几千米高度.该段的主要任务是消除较大的初始水平速度.根据导航结果，按照一定的制导律控制着陆器的轨道和姿态，使着陆器速度减小到预定值并到达期望的着陆区域上空.

2）调姿下降段.从距月面高度几千米到一百米左右.该段的主要任务是调整着陆器姿态为垂直向下.根据导航结果，按照一定的制导律控制着陆器的轨道和姿态，使着陆器到达预定高度的速度接近于零，姿态接近垂直向下，且保证太阳帆板指向预定方向.

3）悬停避障段.从距月面高度一百米左右到几十米.该段的主要任务是在一百米左右高度处，姿轨控发动机工作使得着陆器处于悬停状态，成像敏感器对着陆区域成像，GNC选择安全着陆区域；然后，通过水平和垂向控制使着陆器平移下降至所选着陆区域上方预定高度.

4）缓速下降段.从距月面高度几十米到几米.该段的主要任务是悬停避障结束后，按照一定的制导律控制着陆器的轨道和姿态，使得着陆器到达预定高度的速度接近于零，且保证着陆器在所选安全着陆区域上方.

5）自由下落段.从距月面高度几米到着陆到天体表面.该段采用关机自由落体方式.

图1 月球软着陆过程示意图Fig.1 Lunar soft landing sketch

2 月球软着陆导航敏感器的配置

月球软着陆自主导航系统主要包括：IMU（陀螺和加速度计）、测距敏感器、测距测速敏感器、成像敏感器以及GNC计算机等.为了满足自主快速故障诊断和冗余设计的需求，IMU配置了6个陀螺和6个加速度计，任何3个陀螺都可以完成姿态的测量，任何3个加速度计都可以完成非引力加速度的测量.测距敏感器用于测量着陆器相对月球表面的距离；测速敏感器用于测量着陆器相对于月球表面的速度.为了适应月球着陆过程的大姿态角变化，设置了4个测距测速波束，每个波束可以独立测量，保证至少3个波束可以打到月面上.记4个测距测速波束为L1～L4，其安装如图2～3所示，L1沿着陆器 Z轴方向，L4沿X轴方向，L2、L3在XOZ平面的投影与X轴和Z轴成45。，L2在YOZ平面的投影与Y轴和Z轴成45。，L3在YOZ平面的投影与-Y轴和Z轴成45。.成像敏感器用于对月球表面成像.GNC计算机用于接收各种敏感器的测量信号并利用导航算法进行处理，给出导航结果.

图2 初始着陆时刻的敏感器指向Fig.2 Sensor pointing of initial landing time

图3 垂直下降过程的敏感器指向Fig.3 Sensor pointing of vertical descent process

3 月球软着陆的高精度导航算法

3.1 软着陆惯性导航

月球软着陆惯性导航算法［2］如图4所示.轨道初值利用地面深空网确定；姿态初值由其他姿态敏感器提供.这样，利用IMU测量信息，就可以确定着陆器的惯性位置、速度和姿态，也可以在测距测速仪不可用的情况下确定相对轨道系的姿态、速度和高度等信息.

图4 惯性导航算法流程Fig.4 Inertial navigation algorithm flow diagram

3.2 高精度本体系的月心方向确定

利用测距仪提供的3个以上（含3个）视线距离进行测量，可以获得测距仪第 i个视线指向测得的距离为ρi（ i=1，2，…，n ），n为测距仪的视线方向个数；根据测距仪的安装确定测距仪的指向在探测器本体系的方向矢量为［abi，bbi，cbi］T.

（1）主减速段的月心方向确定方法

利用惯性导航算法给出的轨道和姿态信息，根据测距仪在着陆器本体系的指向，很容易确定测距仪指向月面点的经纬度；根据先验的地形信息可以确定当地月面地形高程信息，即确定测距仪指向点与月心的距离Ri，取月心和月面测距仪指向点在探测器本体系的坐标为（xb0，yb0，zb0）和（xbi，ybi，zbi），则有

根据测距仪的安装和测量，则有

可见，要计算出 （xb0，yb0，zb0），至少需要3个视线指向距离测量 （n ≥3 ）.由于式（2）是非线性方程组，因此，只能采用非线性方程的数值解法.这里采用高斯-牛顿法求解， （xb0，yb0，zb0）的初值利用惯性导航配以测距测速修正算法给出的惯性位置（xI，yI，zI） 和姿态确定探测器本体坐标系的月心位置初值 （x′b，y′b，z′b）=Cbi（ xI，yI，zI），Cbi为从惯性坐标系到探测器本体坐标系的转换矩阵.根据测距敏感器视线指向几何关系确定的方程组形态较好，高斯-牛顿算法几次迭代就可以收敛，而且n=3，因此，整个算法计算量很少.

于是，可以得到探测器本体坐标系的月心位置rb=［xb0，yb0，zb0］T，并计算本体系的月心方向rb0= rb/rb.

（2）其他着陆段的月心方向确定方法

一旦调姿下降段探测器完成姿态调整后，光学成像敏感器就可以对月面特定区域进行成像，获取月面图像信息.于是，可以匹配获取月面图像和存储在探测器上的图像，确定测距仪指向月面点的位置信息（3个以上）.

如图5所示，构造导航参考坐标系，一个测距仪指向月面点O，O为坐标原点，另一测距仪指向月面点A的矢量为X轴，O、A、B 3点确定的平面法线为Z轴，Y轴构成右手坐标.则利用测距仪的测量数据和安装信息可以构造导航参考坐标系，即可确定本体系与导航参考坐标系的转换关系.同样，可以利用匹配获得的月面点位置信息构造导航参考坐标系，进而确定导航参考坐标系的月心方向，于是可以确定本体系的月心方向.

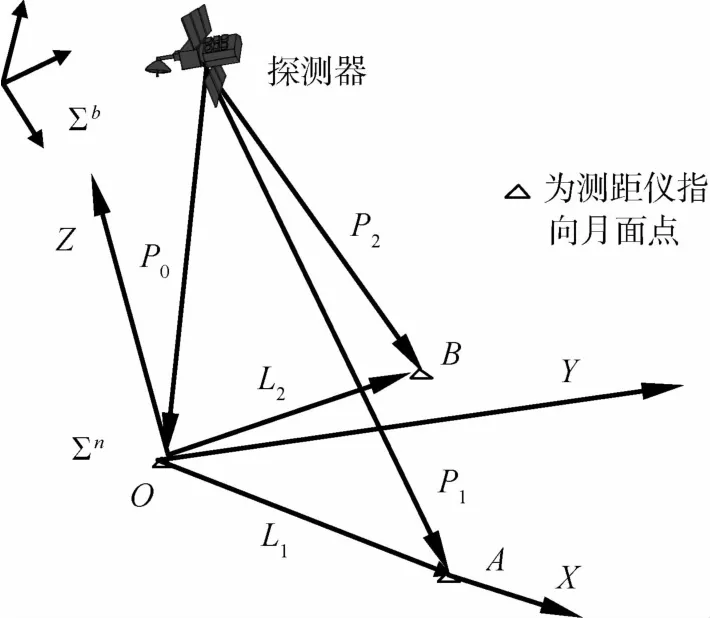
图5 导航参考坐标系Fig.5 Navigation reference coordinate system

对于悬停避障段和缓速下降段，为了精确到达着陆点，探测器需要高精度的相对着陆点位置信息.这时可以把选定的着陆点经过匹配给出着陆点的位置信息，根据每次建立的导航参考坐标系实时更新在本体系的着陆点位置，提供高精度的探测器相对着陆点位置信息.

3.3 高精度的姿态、速度和高度确定

取测速仪3个非共面波束的速度观测量为vc=［vc1，vc2，vc3］T，测速仪 3个波束安装指向分别为vc1b，vc2b，vc2b，则有

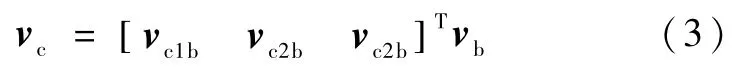
取eox，eoy，eoz分别表示轨道系的3个轴的单位矢量，则利用本体坐标系的观测量构造出轨道系的3个坐标轴矢量为

则本体系相对轨道系的姿态矩阵Cbo为至此，就可以确定探测器本体系相对轨道坐标系的姿态、轨道坐标系的三维速度矢量（记为vo=CTbovb）.

利用本体系的月心方向（rb0）和测距仪本体系的任意一个波束指向（lbi=［abi，bbi，cbi］T）确定两者的夹角关系：cosθi=lbi·rb0，根据测距仪获取的本体系视线距离 ρi确定探测器相对天体表面的高度h=ρicosθi.

4 月球软着陆的制导与控制方法

考虑到高精度导航算法提供的速度和姿态信息都是相对于轨道坐标系的，因此，主减速段和调姿下降段分别采用常推力显式制导和重力转弯制导控制探测器的高度和速度；为了保证探测器能够精确到达着陆点，悬停避障段和缓速下降段采用比例误差反馈制导律；选取轨道坐标系作为姿态参考坐标系，姿态控制采用相平面，这样就保证了姿态估计和控制精度，也保证了速度和高度的控制精度.

4.1 制导律

主减速段采用常推力显式制导律［3］，制动发动机工作于全推力状态，制导控制量为两个推力方向角ψ和φ的显式表达式.在轨道坐标系垂直面和水平面内，根据各加速度矢量之间和速度矢量之间的几何关系，可得出作为控制量的两个推力方向角的表达式

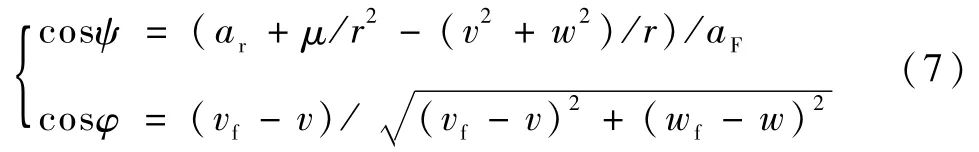
其中，aF为推力加速度，ar为径向加速度，

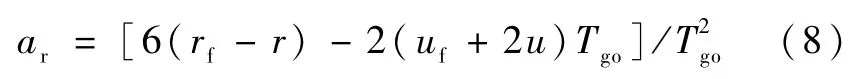
其中，u，v，w表示轨道坐标系中的速度分量，μ表示月球引力常数，r表示着陆器相对月心的距离，uf，vf，wf表示主减速段终端的速度分量，rf表示主减速段终端着陆器相对月心的距离.假设，在燃耗最优的条件下，制动推力主要用来抵消着陆器的水平初始速度，由此，剩余时间的表达式为

其中，aH为推力加速度水平分量.

调姿下降段采用重力转弯制导［3］，基本思想是通过姿控系统将制动发动机的推力方向与着陆器速度矢量的反方向保持一致，进行制动减速，末端达到速度为零，姿态垂直向下.

悬停避障段和缓速下降段采用比例误差反馈制导律［4］，制导需要有速度和位置反馈，垂向加速度反馈也是有益的.

式中：K*，*分别表示各个控制方向的增益系数，其中，ve表示垂向，h表示水平方向，t表示制导目标；a、v和r分别表示加速度、速度和位置.对于水平方向，如果需要移动的距离较大，则只进行速度控制.

4.2 姿态控制方法

姿态控制采用相平面控制，并采用了姿态控制参数化方法［5］解决快速姿态机动问题.姿态控制结构如图6所示.姿态机动逻辑的主要目的是在姿态机动角度很大的情况下，控制着陆器沿误差姿态四元数的方向矢量以最大姿态机动角速度向目标姿态旋转.图中，qCMD表示目标姿态四元素，ωCMD表示目标姿态角速度，qNAV表示估计的探测器当前姿态四元素，ωNAV表示估计的探测器当前姿态角速度，θERR表示姿态角误差，ωERR表示姿态角速度误差，tON表示相平面控制输出的喷气脉宽.

5 数学仿真结果

利用文献［1-3］给出的仿真条件，针对给出的月球软着陆自主导航与控制算法进行了数学仿真，仿真结果如图7～9所示.着陆高度、速度和姿态曲线分别如图7、8和9所示，可以看出，测距仪测距信息引入后，导航高度很快收敛到实际高度；测速仪测速信息引入后，导航速度很快收敛到实际速度；测距测速信息引入后，导航姿态角能够收敛到接近实际姿态角，导航姿态角误差没有随时间增大而增大.同一条件下，与直接采用惯性导航确定姿态和月心方向的方法相比，提出的高精度自主导航与控制方法在姿态和速度、高度确定和控制精度都有一定提高.

图6 姿态控制结构Fig.6 Attitude control structure

图7 着陆高度曲线Fig.7 Landing altitude curve

图8 着陆速度曲线Fig.8 Landing velocity curve

图9 着陆姿态曲线Fig.9 Landing attitude curve

6 结 论

针对高精度月球软着陆的需求，本文研究了一种月球软着陆的高精度自主导航与控制方法.该方法根据测距波束视线相对月面的几何关系，确定本体系的月心方向，组合利用测速仪获取的本体系三维速度确定本体系相对轨道系的姿态、速度及高度，并根据确定的参数性质选取了适应的制导和控制方法.研究表明该方法可以提高月球软着陆姿态、速度与高度的估计和控制精度.

［1］ Wang D Y，Huang X Y.GNC system scheme for lunar soft landing spacecraft［J］.Advances in Space Research，2008，42（2）：379-385

［2］ 王大轶，黄翔宇.基于IMU配以测量修正的月球软着陆自主导航研究［J］.宇航学报，2007，28（6）：1544-1549 Wang D Y，Huang X Y.Research on the autonomous navigation based onmeasurement-updated IMU for Lunar soft landing［J］.Journal of Astronautics，2007，28（6）：1544-1549

［3］ 王大轶.月球软着陆的制导控制研究［D］.哈尔滨工业大学，2000Wang D Y.Research on the guidance and control of lunar soft landing［D］.Harbin Institute of Technology，2000

［4］ Ronald R S.Powered descent trajectory guidance and some consideration for human lunar landing［C］.The 30thAnnual AAS Guidance and Control Conference，Breckenridge，Colorado，2007

［5］ Michael C J.A parameterized approach to the design of lunar lander attitude controllers［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Keystone，Colorado，2006

Pinpoint Autonom ous Navigation and Control for Lunar Soft Landing

HUANG Xiangyu1，2，ZHANG Honghua1，2，WANG Dayi1，2，LI Ji1，2，GUAN Yifeng1，2，WANG Pengji1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China）

A pinpoint autonomous navigation and control algorithm for lunar soft landing is presented in the paper.In the algorithm，first，the direction of landing spacecraft relative to the lunar center is determ ined according to the geometry relation of several ranging beams relative to the lunar surface.Second，attitude，velocity and altitude relative to the orbit reference frame are determined by combining the velocity vector provided by the velocimeter in the body reference frame.Third，the adaptive guidance and controlmethod is selected based on the character of determined parameter.The algorithm can determine and control parameters of attitude，velocity and altitude based on direct measurement data and can improve the estimation and control accuracy of attitude，velocity and altitude，and can’t be affected by the inertial navigation error.Finally，the presented algorithms are validated by mathematical simulations.

lunar soft landing；autonomous navigation；guidance and control

V476

A

1674-1579（2012）02-0005-05

黄翔宇（1976—），男，高级工程师，研究方向为航天器自主导航与制导；张洪华（1963—），男，研究员，研究方向为航天器轨道和姿态控制；王大轶（1973—），男，研究员，研究方向为深空探测航天器自主控制；李 骥（1978—），男，高级工程师，研究方向为航天器导航、制导与控制；关轶峰（1976—），男，高级工程师，研究方向为航天器姿态控制；王鹏基（1976—），男，高级工程师，研究方向为航天器动力学与控制.

2010-09-15

DO I：10.3969/j.issn.1674-1579.2012.02.002