提高零控脱靶量预测精度的一种方法

姬晓琴，崔鑫水

（宇航智能控制技术国家级重点实验室，北京 100854）

提高零控脱靶量预测精度的一种方法

姬晓琴，崔鑫水

（宇航智能控制技术国家级重点实验室，北京 100854）

对于大气层外拦截问题中以零控脱靶量（ZEM—zero effortm iss）作为指标的预测制导方法，其ZEM的预测精度直接影响到最终的拦截任务.在线性化平方反比引力模型下，给出了基于目标轨道坐标系的ZEM预测算法，导出ZEM发生条件，并提出一种提高ZEM预测精度的方法，即通过初值轨道角速率的选取可明显改善算法的预测精度.同时将该算法与地心赤道惯性坐标系下的ZEM预测算法进行了比较研究，数学仿真结果表明该预测算法精度较高，具有一定的工程应用价值.

大气层外拦截；零控脱靶量；ZEM预测算法；相对运动；目标轨道坐标系

反战术弹道导弹系统一般采用分层防御体系，其中以动能武器技术为代表的高层拦截反导系统尤为重要，已经成为各国竞相发展战区弹道导弹防御系统的主要技术之一.自20世纪70年代以来，美国已经先后研制并试验了多种类型的动能拦截弹，包括反卫星用的空基和地基动能拦截弹、防御弹道导弹的天基、地基和海基动能拦截弹，可在大气层内或大气层外对目标实施拦截.大气层外拦截中制导律设计方法的有效性是关系到拦截器所释放出的动能杀伤器碰撞杀伤来袭目标需要付出代价的评估标准［1-2］.对于以零控脱靶量（ZEM，zero effortmiss）作为指标的预测制导方法，其ZEM的预测精度直接影响到最终的拦截任务.高精度的ZEM数值积分算法受到弹载计算机速度的限制，而现有的ZEM解析或快速预测算法因精度不够高较难应用到大气层外具有上千千米的拦截情况.本文在线性化平方反比引力模型下，给出了基于目标轨道坐标系的ZEM预测算法，在此基础上提出了一种提高预测精度的方法，该方法通过初值轨道角速率的选取可明显改善算法的预测精度，并且预测精度比较稳定，具有一定的工程应用价值.

1 坐标系定义

1.1 问题提出

首先引入两个坐标系：地心赤道惯性坐标系OeXYZ和目标轨道坐标系OTxyz，其定义如下.

地心赤道惯性坐标系OeXYZ（简称惯性系）：坐标原点在地心；OeX在赤道平面内，指向春分点；OeZ垂直于赤道平面，与地球自转轴重合；OeY与OeX、OeZ组成右手坐标系.

目标轨道坐标系OTxyz（简称轨道系）：坐标原点在目标质心；OTx位于轨道面内，指向飞行方向为正；OTz沿地心矢径方向，指向地心为正；OTy与OTx、OTz组成右手坐标系.

2 惯性系下的ZEM预测算法

本节给出地心赤道惯性坐标系下基于线性化平方反比引力模型［1，3-4］的ZEM预测算法.

对于终端时间非固定的大气层外拦截问题，预测制导控制就是通过实时预测脱靶时刻和ZEM来产生制导指令.其中对于非机动目标拦截问题，零控脱靶量可以表述为拦截器与目标在仅受引力场作用下被动飞行至脱靶时，两飞行器间的最小相对位置矢量［5-7］，如图1所示，图中同时也标出了上述两个坐标系的示意图.

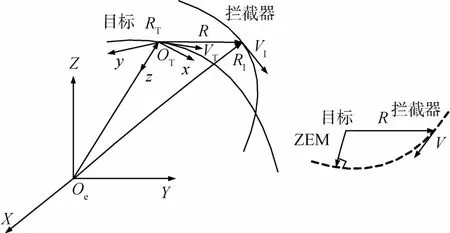
图1 零控脱靶量示意图Fig.1 Sketch of zero miss distance

在大气层外拦截器与目标的运动方程可表示为：

式中：RI、RT分别表示拦截器、目标位置矢量；rI、rT分别表示拦截器、目标位置矢量的大小；

μ表示地球引力常数.

则目标相对于拦截器的相对运动方程可表示为：

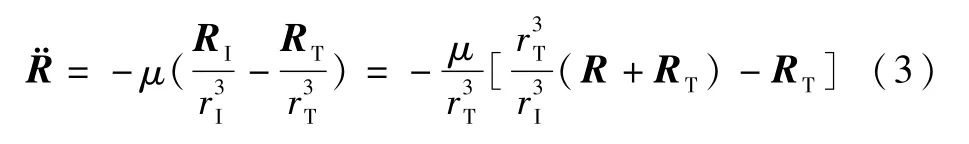
式中R=RI-RT，记R的大小为r.

上式是线性时变二阶微分方程，若目标在整个飞行阶段位置变化不大，则可以利用一个常矢量RTc来代替变化的RT，以得到上式的解析解.令RTc=RT0+crR，其中cr为常数，RT0为初始时刻目标矢量.

式中：

由式（6）可得线性定常齐次状态方程的解为：

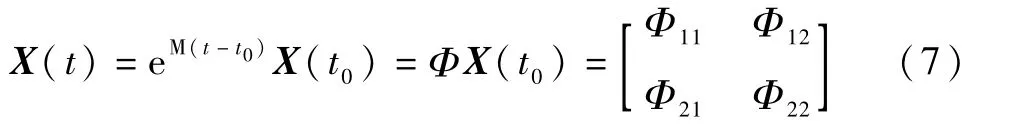
ZEM发生时刻tf（即脱靶时刻）应有：

通过二分法、牛顿法等数值方法求解ZEM发生时刻tf，可取tf的迭代初值为：

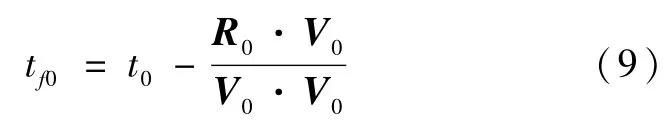
将tf代入式（7），可得ZEM的预测值为：

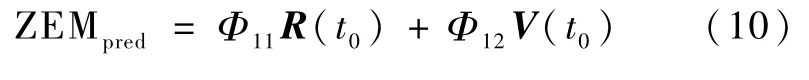
将式（4）代入式（3），得：

3 轨道系下的ZEM预测算法

下面给出轨道系下基于线性化平方反比引力模型的ZEM预测算法.取目标轨道坐标系作为相对运动坐标系，则式（3）可写为：

若令Rrel=［x y z］T，将式（11）写成标量形式，得到一组线性时变微分方程组：

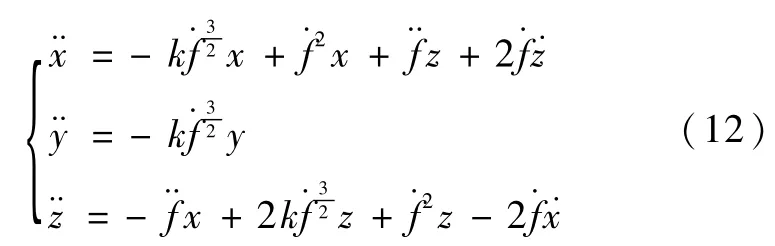
因OTxz平面为轨道平面，OTy为轨道负法向，为方便起见，可重记 Rrel=［x z y］，ω=［RrelVrel］T，给定初始条件，通过变量变换可得到式（12）的解析解［8］：

其中：

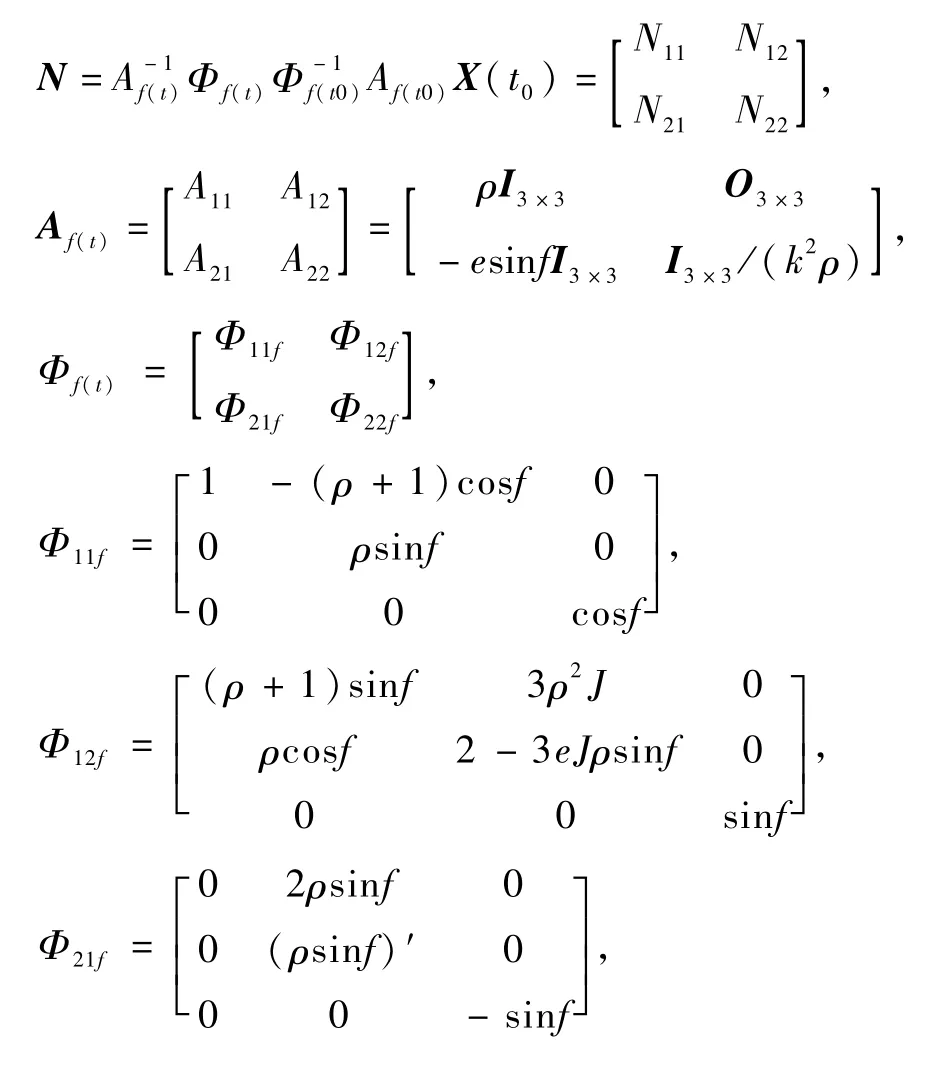
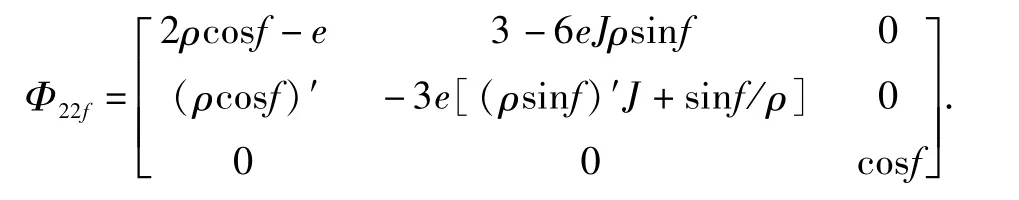
其中，ρ=1+e cos f，J=k2（t-t0），e为轨道偏心率.

根据惯性系ZEM发生条件式（8），可导出目标轨道坐标系的ZEM发生条件：

通过数值方法求解上式ZEM发生时刻tf，将tf代入式（14），可得ZEM的预测值为：

tf的迭代初值tf0取法同上.

综上所述，因式（13）是解析解的形式，故轨道系ZEM预测算法的精度应优于惯性系ZEM预测算法.但经数学仿真计算结果表明：在常数cr=0时，前者精度确实优于后者，但在 cr≠0时，若不对式（13）进行改进，其精度并不理想.经研究发现类似上节将RT取为常矢量的方法，将初值轨道角速率预测精度，具体思路如下：

又因

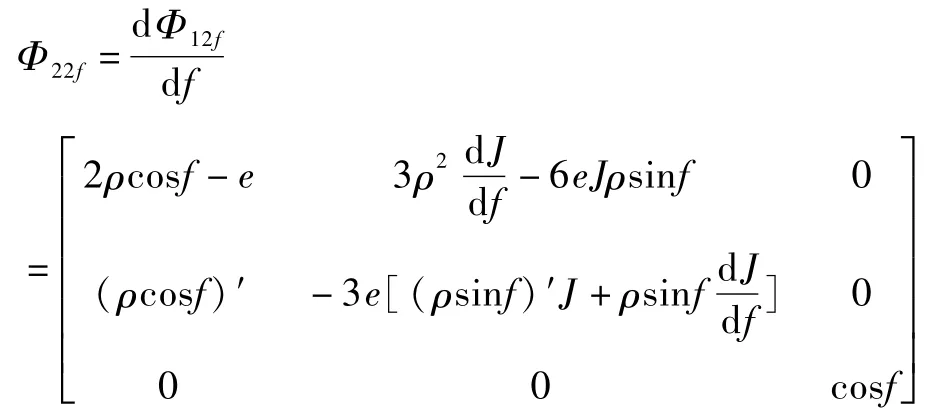
故可将Φ22f的初值改写为：

其中ρc=1+e cos fc，fc=f0+cf（ft0-f0），cf为常数，ft0为由脱靶时刻的迭代初值tf0计算得到的真近点角.这样通过选择c改变f的值，也即的值可得到较好的预测精度，这将在下节通过数学仿真进行详细说明.

4 预测算法精度分析

本文对轨道系和惯性系下的两种ZEM预测算法进行了数学仿真研究及精度比较分析，同时对算法中常数cf（cr）对预测精度的影响也进行了简单仿真研究.

4.1 仿真条件

设拦截器和目标的初始相对距离约为1500km，目标初始状态如表1所示.根据初始相对速度的大小设置了6种拦截器初始状态，为简单起见，拦截器初始位置参数：RT0=［702.9 -8323.1 -2703.3］Tkm不变，仅速度参数变化，如表2所示.

表1 目标初始状态（地心赤道惯性坐标系）Tab.1 Initial target state（ECI）

表2 拦截器初始状态（地心赤道惯性坐标系）Tab.2 Initial interceptor state（ECI）

4.2 算法精度比较分析

令Δtf、Δrf、Δvf分别表示预测脱靶时刻误差、位置误差及速度误差.两种预测算法精度比较见表3所示.表中的预测结果皆取cf=0.4，cr=0.5，此时RTc=RT0+0.5R0=（RT0+RI0）/2，其顶点为RT0与RI0所组成的平行四边形的中心.

表3 预测算法精度比较Tab.3 Accuracy comparsion of predictive method

从表3可看出，随着相对速度 v0的增大，脱靶时刻tf的缩短，两种预测算法的精度都在逐渐提高.在cf=0.4，cr=0.5情况下，前者的精度显然优于后者，且在相对速度较低时尤为明显：Δtf精度约提高70%以上，状态6达到两个数量级，由131.2ms提高到1.2ms；Δrf精度约提高40%以上，状态1达到58%，由69.979km提高到28.908km；Δvf精度约提高30%以上，状态1达到70%，由213.88m/s提高到60.535m/s.

另外，本文对拦截器和目标的初始相对距离为2000km、2500km的情况也进行了两组仿真计算，结果表明在相对速度相同时，两个预测算法的预测精度都随距离的缩短而提高.

4.3 常数cf（cr）对算法精度的影响

以拦截器的第4、第6种初始状态为例，cf（cr）取不同值时得到的脱靶时刻误差分别如表4、表5所示.

从表4、表5可看出，对轨道系ZEM预测算法来说cf=0.4时，预测精度较好，且Δrf、Δvf与Δtf的变化趋势基本一致；而对惯性系ZEM预测算法来说，cr=0.5精度较好，但Δrf、Δvf与Δtf的变化趋势并不一致.将所有拦截状态由轨道系算法仿真得到的Δtf、Δrf随 cf的变化曲线绘于图2、图3，原算法的Δtf、Δrf随cr的变化曲线绘于图4、图5.从图2、图3中可看出：（1）相对速度大时Δtf、Δrf曲线相对变化较平缓，相对速度小时曲线相对变化较大；（2）Δtf单调增加且相对每个算例均有正负变化，Δrf在极值点附近变化较剧烈（相对图5）；（3）cf取0.4～0.6时预测精度较好，精度比较稳定.从图4、图5中可看出，cr取值较大时Δtf预测精度较好，而Δrf预测精度较好时cr取0.4～0.6，两者取值范围不一致.

表4 常数cf（cr）对预测精度的影响（状态4）Tab.4 Influence of constant cf（cr）on prediction accuracy（state 4）

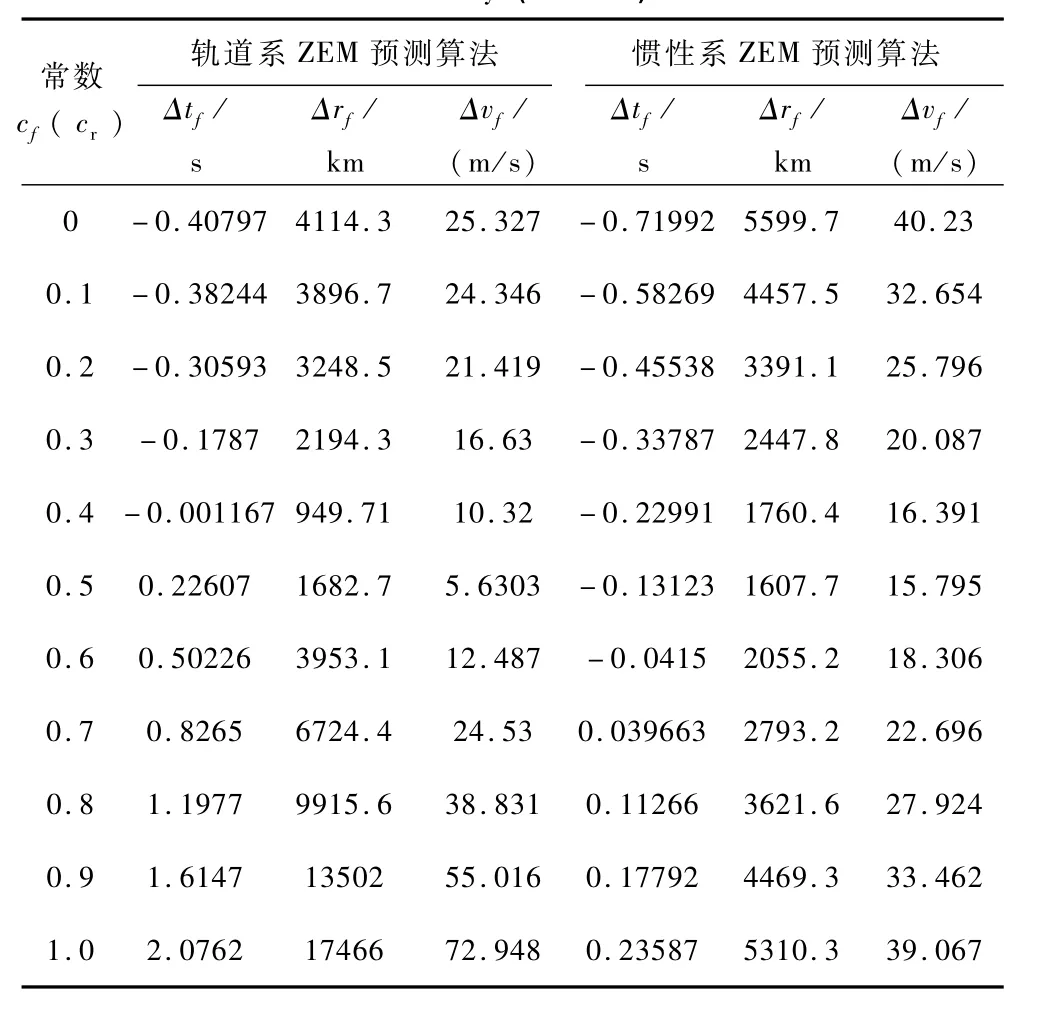
表5 常数cf（cr）对算法精度的影响（状态6）Tab.5 Influence of constant cf（cr）on prediction accuracy（state 6）

图2 Δtf随cf的变化曲线Fig.2 Δtfvarying with cf

图3 Δrf随Δrf的变化曲线Fig.3 Δrfvarying withΔrf

图4 Δtf随cr的变化曲线Fig.4 Δtfvarying with cr

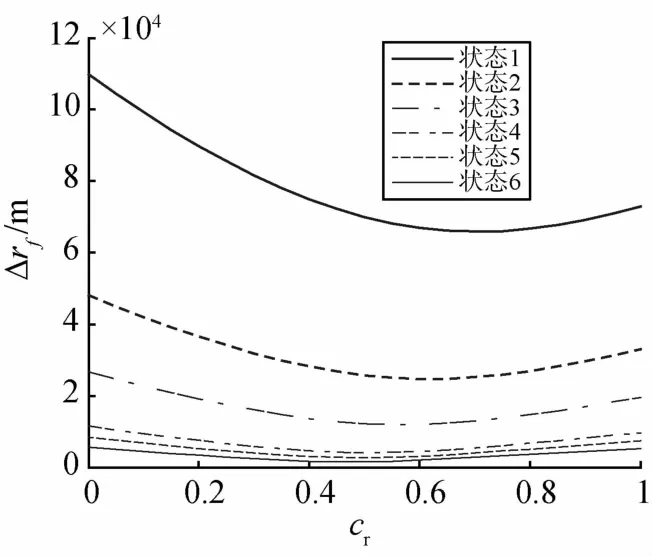
图5 Δrf随cr的变化曲线Fig.5 Δrfvarying with cr

4 结 论

本文在线性化平方反比引力模型下，给出了基于目标轨道坐标系的ZEM预测算法，导出ZEM发生条件，并提出了一种提高预测精度的方法，即通过选取初值轨道角速率的方法可明显提高算法的预测精度，并且稳定性比较好.数学仿真结果表明：

1）由于轨道系下的ZEM预测算法是解析算法，在cf、cr同时为零的情况下，其精度高于惯性系下的预测算法；

2）轨道系下的ZEM预测算法预测精度随相对速度的增大、相对距离的缩短而提高；

3）惯性系下的ZEM预测算法预测精度虽可通过cr的选取得到提高，但cr的稳定性不强，预测精度随初始条件的变化较大；

4）本文提出的轨道系下改变 cf也即改变初值轨道角速率的方法，可明显改善算法的预测精度，且cf在0.4～0.5之间取值时预测精度比较稳定.

需要说明的是，本文只是研究出一种提高算法预测精度的方法，但对该方法的稳定性从理论上还未予证明，这是后续需要进一步研究的内容.另外，现已进行的进一步仿真表明cr的稳定性与拦截器和目标的相对位置有关，所以实际应用该算法时应具体问题具体分析.

［1］ 郑立伟.预测制导理论在飞行器再入与大气层外拦截中的应用［D］.哈尔滨工业大学，2007 Zheng LW.Theory of predicative guidance with app lication to reentry and exoatmaspheric interception［D］. Harbin Institute of Technology，2007

［2］ 刘真.动能杀伤拦截器KKV［J］.地面防空武器，2004（3）：10-12 Liu Z.Kinetic kill vehicle KKV［J］.Land-Based Air Defence Weapons，2004（3）：10-12

［3］ 林来兴.空间交会对接技术［M］.北京：国防工业出版社，2003 Lin L X.Space rendezvous and docking technology［M］.Beijing：National Defence Industry Press，2003

［4］ 郗晓宁，王威，高玉东.近地航天器轨道基础［M］.长沙：国防科技大学出版社，2003 Xi X N，Wang W，Gao Y D.Fundamentals of near-earth spacecraft orbit［M］.Changsha：National University of Defense Technology Press，2003

［5］ Newman B.Spacecraft intercept guidance using zero effortmiss steering［R］.AIAA 93-3890，1993

［6］ Newman B.Robust conventional based midcourse guidance for spacecragt intercepts［C］.The Amarican Control Confence，Seattle，Washington，June 1995

［7］ Newman B.Strategic interceptmidcourse guidance using modified zero effortmiss steering［J］.Journal of Guidance，Control，and Dynam ics，1996，19（1）：107-112

［8］ Kazuki H.A new approach for spacecraft rendezvous and fly-around control on elliptic Orbits［C］.The 56thInternational Astronautical Congress，Fukuoka，Japan，2005

A M ethod for Im p roving Prediction Accuracy of Zero Effort M iss

JIXiaoqin，CUIXinshui
（National Key Laboratory of Science and Technology on Aerospace Intelligent Control，Beijing 100854，China）

For the predictive guidance with zero effortmiss（ZEM）taken as a performance objective for exo-atmospheric interception problem，the prediction accuracy of ZEM directly influences the completion of terminal interceptmission.In this paper，a ZEM forecastingmethod based on the target-centered orbit frame is introduced by using the linearized inverse square gravitymodel.The condition of ZEM occurrence is derived and one method for improving prediction accuracy of ZEM is also put forward，which can distinctly improve the prediction accuracy by choosing the initial orbit angular velocity.Moreover thismethod is compared with the one based on ECI frame by simulation.The results indicate that the improved one has higher accuracy and certain value to practical application.

exo-atmospheric interception；zero effort miss；ZEM forecasting；relative motion；targetcentered orbit frame

V448.23

A

1674-1579（2012）02-0024-06

姬晓琴（1971—），女，高级工程师，研究方向为飞行器导航、制导与控制；崔鑫水（1937—），男，研究员，研究方向为飞行器导航、制导与控制.

2011-07-12

DO I：10.3969/j.issn.1674-1579.2012.02.005