基于视线制导的空间交会停靠控制方法*

王 颖，解永春

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

学术研究

基于视线制导的空间交会停靠控制方法*

王 颖1，2，解永春1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

空间交会停靠段的控制经常采用的一种方法是基于视线位置信息的平行接近法.对纵向控制中的非线性滑动模态控制方法进行了研究和改进，考虑了视线角对纵向控制的耦合作用，增加了耦合项，并进行了存在性和稳定性分析.对于横向和纵向同时协调控制，提出一种多变量互相耦合的非线性滑动模态视线制导控制方法，并对同时协调控制进行了存在性和稳定性分析.

交会停靠；平行接近法；非线性滑动模态

空间交会停靠段的控制经常采用基于视线位置信息的平行接近法.文献［1］给出了平行接近法的3种不同的定义.在采用基于视线位置信息的平行接近法中广泛应用的是比例制导［2-3］.可以采用比例制导方法，但不能把比例制导用作建立平行接近法的基本原理，任何一种制导方法都可以建立相对运动的原则，并可借助不同的控制规律加以实现.文献［1］中给出了平行接近法的几种控制方法.根据理论研究和实验研究的结果，能够满足建立简单而有效的控制系统要求的最合适的交会控制方法是采用发动机开关控制的平行接近方法.这一方法被成功地用于“联盟”号飞船的接近控制系统中.沿视线的纵向运动控制按下述规律进行：，也可以称为滑动模态，将滑动模态平移，即增加了阻尼项［4］.本文对这种滑动模态控制进行了研究，并对此进行了改进，考虑了视线角β对纵向控制的耦合作用，增加了耦合项，改进后k1、k2、k3为大于零的正常数，并证明了改进后的滑动模态控制的稳定性.

对于横向控制，一般采用死区控制方法控制视线转动的角速度［1-2］，这种控制方法只能消除视线转动的角速度，在消除视线角速度的同时，视线角 β会发生变化.由于没有对视线角 β进行控制，所以死区控制方法不能控制视线角 β的变化，这样在纵向采用非线性的变结构控制，只能精确控制相对距离.如果相对距离 ρ≠0，视线角 β发生变化，则追踪器可能位于以目标器为中心以ρ为半径的圆周上任意一点，这时需要用 β的值来准确确定追踪器的位置，所以本文对横向和纵向采用同时协调控制，提出视线角和视线距离互相耦合的多变量非线性滑动模态视线制导控制方法，并证明了控制系统的稳定性.

1 视线坐标系及其相对运动方程

1.1 视线坐标系Oξζη

假设航天器为刚体，目标航天器运行在圆轨道或近似圆轨道上，其姿态保持对地定向，追踪航天器一般运行在小偏心率的椭圆轨道上，不作变轨机动时其姿态保持对地定向.

RVD轨道坐标系Oxyz的原点O在目标星的质心，y轴沿轨道矢径方向，指向目标星，x轴在轨道平面内与y轴垂直，沿轨道运动的反方向，z轴垂直于轨道面，与x轴和y轴成右手坐标系.视线坐标系Oξζη的Oξ轴的方向是从目标航天器质心到追踪航天器质心的视线方向，其他两轴的定义由RVD轨道坐标系到视线坐标系经过3β-2α转序旋转得到.

α为视线与其在目标轨道平面上的投影之间的夹角，称为偏离角.

β为该投影与x轴之间的夹角，称为视线角.

1.2 在视线坐标系中的相对运动方程［1］

设目标航天器在圆轨道上运动，在近距离的情况下，追踪航天器和目标航天器在同一个轨道面上，当目标航天器和追踪航天器共面时，α=0，则追踪航天器和目标航天器的相对运动方程如下：

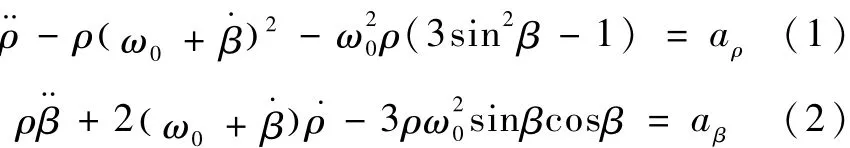
式中，ω0为目标航天器的轨道角速度，ρ为相对距离为相对速率为视线角速度，β为视线角.

2 相对运动方程的控制方法

2.1 横向和纵向分时控制

（1）视线速率（Ωρ）的控制［1］

控制视线转率Ωρ的目的是使得追踪航天器沿视线方向接近目标航天器，控制方法为：

采用非线性滑动模态控制，滑动模态为：

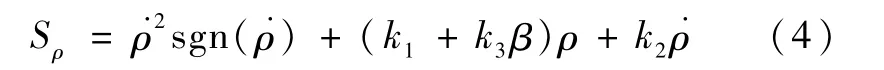
式中，k1、k2、k3为常数，k1、k2、k3的符号为正，当ρ＞0时＜0，β≥0且有界，0≤β≤2π，选择 k1和 k3，使得k1+k3β＞0.

当β→0，k1+k3β→k1，k1大，在β→0时，有较大的比例系数，会使得过渡过程加快.

2.2 横向和纵向同时控制

（1）视线角 β的控制

横向控制仍然采用变结构控制，因为执行机构为开关工作方式.设计滑动模态为：

式中k＞0.

（2）纵向控制与2.1节中的视线距离和视线距离速率相平面控制律相同.

2.3 滑动模态存在区域

（1）横向控制

当Sβ＜0，＞0，aβ=Fβ，则：

所以滑动模态的存在区域为：

（2）纵向控制

同理，可以得到纵向非线性滑动模态的存在区域：

2.4 稳定性

（1）横向和纵向分时控制

利用等效控制，可以得到纵向控制系统的等效系统为：

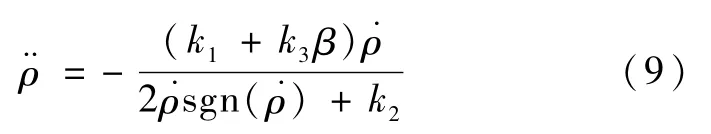
选择Lyapunov函数为：

因为：k1、k2、k3为正常数动模态外，设Lyapunov函数为时＜0，且k1+k3β＞0.

（2）横向和纵向采用同时控制

根据等效控制，可以得到横向控制系统的等效的控制系统：

纵向控制系统的等效控制系统为式（8）.

根据横向控制的滑动模态（5），在滑动模态上有：

把式（14）代入式（13）中，得到：

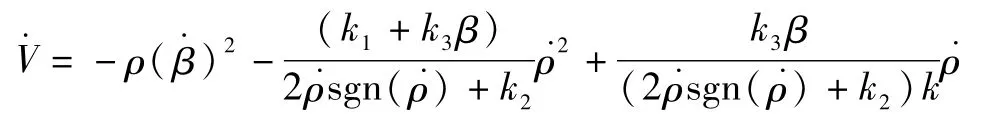
横向控制的等效控制量：

在视线角的滑动模态中引入ρ，滑动模态为变斜率的滑动模态.从式（15）中可以看出，分母上没有ρ，则等效控制量不会因为 ρ趋向于零而趋向于无穷大.

3 仿真结果

为了避免发动机的频繁开关，在相平面 ρ-˙ρ内，定义两条开关抛物线A，B，将相平面分为3个区域［4］，如图1所示.1区为加速区，当系统在1区时，加速航天器，A为发动机关机线，2区为不控区，发动机关闭，系统在3区时，减速航天器，B为发动机开机线.设置两条开关线，减少发动机的开关次数，在一定程度上削弱了抖振.

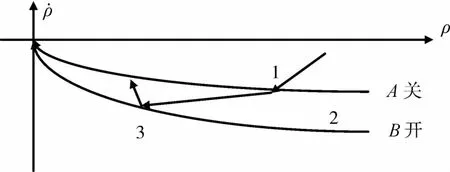
图1 相平面ρ-控制律Fig.1 Phase plane control law ofρ-

对于视线角的控制，也采用如上同样方法加入死区，防止发动机的频繁开关，控制输出有饱和限幅，仿真对象模型考虑了大气阻力和地球扁率的影响.

没有改进的分时控制：横向采用式（3），纵向采用滑动模态S=sgn（+kρ，仿真结果见图2.改进的分时控制：横向采用式（3），纵向采用式（4），仿真结果见图3.同时控制：横向采用滑动模态控制式（5），纵向采用滑动模态控制式（4），仿真结果见图4.

表1 视线制导控制仿真结果Tab.1 Simulation result of line of sight guidance

图2 没有改进的视线制导的仿真结果（竖线表示仿真开始时刻，下同）Fig.2 Simulation result of line of sight（vertical line denotes starting time of simulation）

图3 改进后的视线制导的仿真结果Fig.3 Simulation result of improved line of sight

图4 横向和纵向同时控制的仿真结果Fig.4 Simulation result of control of the angle of the LOS and of the lengthways at the same time

4 结 论

从仿真结果可以看出，在对象模型考虑了大气阻力和地球扁率的影响的情况下，控制结果达到了要求.

2）非线性滑动模态控制系统的鲁棒性很好，因为滑动模态的定义与对象模型无关.在视线坐标系中，相对运动方程为非线性方程，滑动模态也是非线性的，这种非线性的滑动模态控制能减少发动机的开关次数.

横向和纵向同时进行控制时，同时控制的稳态精度比分时控制的稳态精度高，但燃料比之要多.如果要求稳态精度比较高，横向和纵向同时控制方法是可以选择的.

［1］ 林来兴.空间交会对接技术［M］.北京：国防工业出版社，1995 Lin L X.Space rendezvous and docking technology［M］.Beijing：National Defence Industty Publishing Company，1995

［2］ 于绍华.全方位自主交会对接的控制方法［J］.宇航学报，1993，14（3）：10-17 Yu S H.Control schemes for automatic rendezvous and docking［J］.Journal of Astronautics，1993，14（3）：10-17

［3］ 于绍华.空间交会的末端控制模式［J］.宇航学报，1998，19（3）：16-19 Yu SH.Control schemes for terminal spacecraft rendezvous［J］.Journal of Astronautics，1998，19（3）：16-19

［4］ 王颖，吴宏鑫，解永春.空间交会停靠的变结构控制［J］.中国空间科学技术，2001，21（3）：1-5 Wang Y，Wu H X，Xie Y C.Variable structure control of space rendezvous and berthing［J］.Chinese Space Science and Technology，2001，21（3）：1-5

Rendezvous and Berthing Control M ethod Based on Line of Sight Guidance

WANG Ying1，2，XIE Yongchun1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China）

The control of approaching phase of the space rendezvous and berthing often uses the parallel approaching method based on the signal of the line of sight（LOS）position.The nonlinear sliding modal in the longitudinal control is improved by adding the coupled item and the damping item including the LOS angle.Its existence and stability are proved for the relative equations.The coup led multivariable nonlinear sliding modal of the LOS guidance is presented.The existence and stability are proved for the coordinated control.

rendezvous and berthing；parallel approaching method；nonlinear slide modal

V448.22+4

A

1674-1579（2012）02-0001-04

王 颖（1974—），女，高级工程师，研究方向为航天器制导、导航与控制；解永春（1966—），女，研究员，研究方向为智能自主控制方法以及航天器制导.

*国家自然科学基金资助项目（61004058）.

2011-08-20

DO I：10.3969/j.issn.1674-1579.2012.02.001