开槽管型药柱燃烧规律的研究①
2012-08-31相升海魏开新李世鹏张伟宏李志秋徐文龙
相升海,魏开新,李世鹏,张伟宏,李志秋,徐文龙
(1.沈阳理工大学装备工程学院,沈阳 110159;2.北京理工大学 宇航学院,北京 100081;3.长沙机电产品研究开发中心,长沙 410100)
0 引言
固体火箭发动机装药燃烧规律的研究是内弹道计算的关键。发动机装药燃烧规律主要包括药柱几何形状的选取和燃面的计算[1]。常用的药柱主要有管型、星孔型、锥柱型、球型、扇面型、翼柱型等[2-4]。近年来,开槽管型药柱作为一种新型药柱已被应用于火箭弹和导弹中。开槽管型药柱不仅能在较短的时间内提供较大的初始燃烧面积,还可以通过对设计参数的调整获得所需要的燃烧规律。国内对开槽管型药柱的研究比较少,公开的文献也有限。文献[5]对开槽管型药柱进行了减面燃烧规律的研究,并对开槽数、槽长对燃面变化的影响进行了研究。文献[6]对美国“爱国者PAC-3”型导弹主发动机装药药型进行反设计,分析计算了该药型的优点,并比较了开四、五、八槽3种药柱的压强-时间曲线,但文献[5-6]中的药柱深槽处均为直角过渡。
本文对开槽管型药柱进行研究,导出开槽管型药柱燃烧面积的计算公式,分析并总结开槽管型药柱的燃烧规律,最后给出开五、六、七槽管型药柱燃烧规律的算例。
1 数学模型
图1给出了开槽管型药柱的剖面图,外径为D,药长为L,开槽数为N,内孔径为d,槽深为L1,端面弧槽半径为r,槽长为h,肉厚为e。由于开槽的对称性,选取其中一槽作为研究对象,肉厚e的变化为ei(i=1,2,…,5)。
另外,对开槽管型药柱采用几何燃烧定律,它基于以下假设:
(1)组成成分及物理化学性能均匀一致;
(2)燃烧表面各点燃烧条件相同;
(3)全部燃烧表面同时点燃,并沿其法向方向以相同的速度向药柱外部推移。

图1 开槽管型药柱剖面、各个燃烧面及肉厚e的变化Fig.1 Profile of slotted tube grain,all the burning faces and the changes of e
2 开槽管型药柱燃面变化规律
2.1 燃烧过程中关键点的确定
(1)内圆弧消失点e1

(2)槽侧边消失点e2
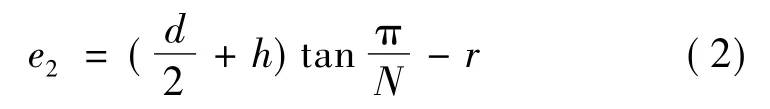
(3)槽顶燃层燃完点e3
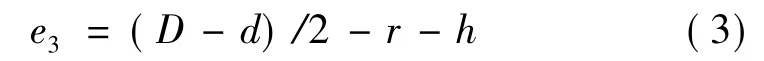
(4)圆柱段燃完点e4

由化简可得

(5)药柱完全燃完点e5

2.2 燃面计算
将开槽管型药柱外侧面包覆,根据药柱的初始燃面及平行层燃烧规律,可将其划分为6个燃烧面(图1),经推导得到各个燃面的面积公式。
(1)端面弧槽面
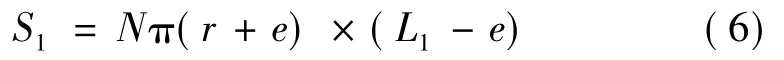
(2)深弧槽面
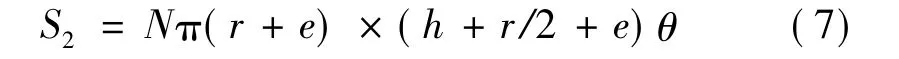
(3)槽侧面

(4)槽内孔圆弧面及圆柱段面

(5)未开槽端面
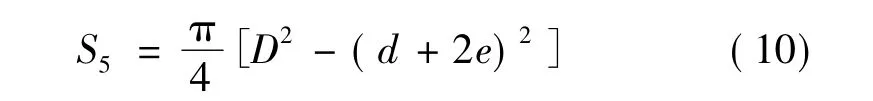
(6)开槽端面
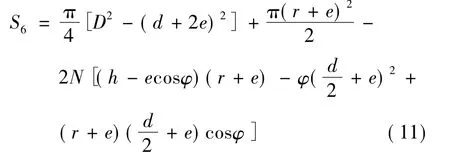
综上可得,开槽管型药柱的总燃烧面积:

2.3 约束方程
为了减少残药,采取几个关键点相等的原则,可得到约束方程:
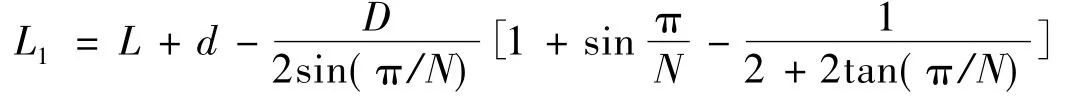
则:

其中:

2.4 燃烧规律
令 f(e)=S,则有
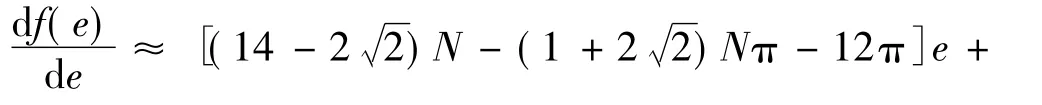

令:
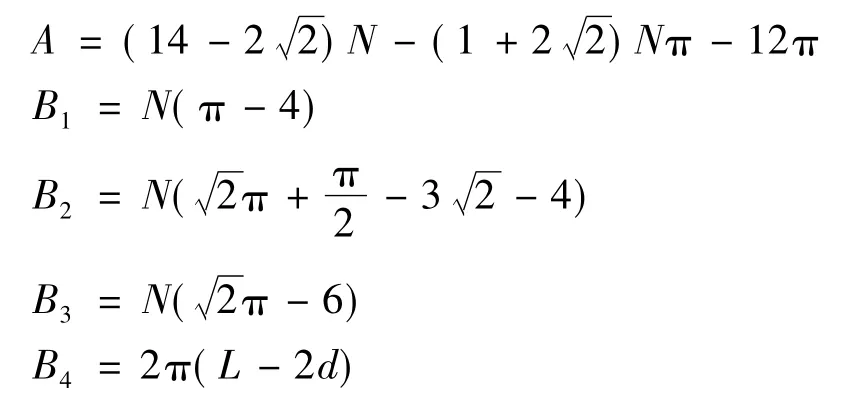
则有
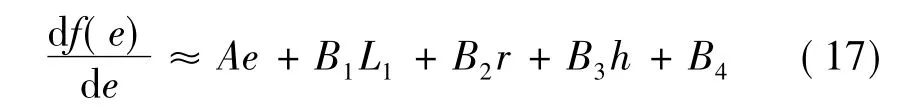
可得:N≈-41.9。因为开槽数必须为正整数,得到的N不满足要求,因此本药柱燃烧规律不具有恒面性。
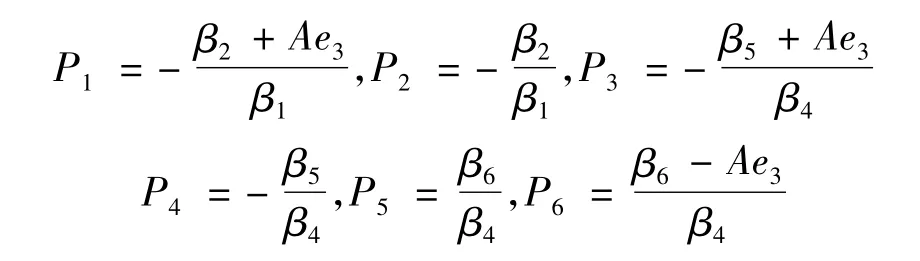
其中:


图2表明:
(1)当L1<P1,燃烧规律呈现增面性;当P1<L1<P2,呈现先增面性后减面性;当L1>P2时,呈现减面性;且L1越接近P1、P2的均值,越接近恒面性。
(2)当r<P3时,燃烧规律呈现增面性;当P3<r<P4,呈现先增面性后减面性;当r>P4时,呈现减面性;且r越接近P3、P4的均值,越接近恒面性。
(3)当h<P5时,燃烧规律呈现减面性,当P5<h<P6,呈现先增面性后减面性;当h>P6时,呈现增面性;且h越接近P5、P6的均值,越接近恒面性。
2.5 相关参数的计算
开槽数分别取N=5、6、7,药柱只改变槽深 L1,其他设计参数以及装药量均相同。
由于药柱的总装药量相同,则开槽部分的总体积V也相同:

可得
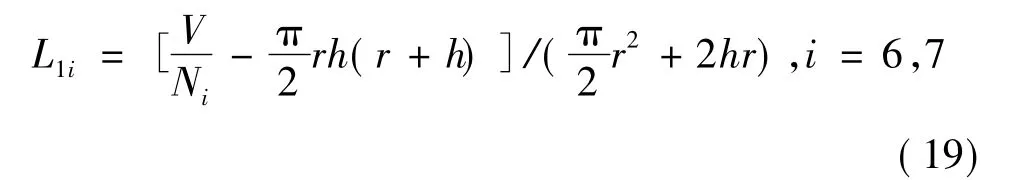
同理,当 N=5、6、7,分别只改变 r、h,其他设计参数及装药量均相同时,可得


3 算例及结果分析
文献[6]给出了美国“PAC-3”导弹主发动机装药药型的设计参数,D=253 mm,L=2 186 mm。
当 N=5,d=134.5 mm 时,由式(3)、式(13)计算可得 e3=45 mm、L15=2 045.6 mm。
当 N=6、7时,由式(18)、式(19)联立可得:L16=1 772.9 mm,L17=1 458.2 mm。
由于药柱模型的实际轴向尺寸较大,本文截取其中一段。图3给出了开槽管型药柱开六槽时燃烧过程中的三维视图。
计算可得临界域的边界值分别为:P15=2 092.9 mm,P16=1 732.4 mm,P17=1 422.3 mm;P25=2 173.7 mm,P26=1 810.4 mm,P27=1 508.6 mm。
比较可知:L15<P15,燃烧规律呈现增面性;P16<L16<P26,P17<L17<P27,燃烧规律呈现先增面性后减面性。且开五槽时槽深小于临界域的最小值,增面幅度较大;开六槽时槽深距离临界域均值较近,增减幅度较小,接近恒面性;开七槽时槽深距离临界域均值较远,增减幅度较大。
另外,分别对r、h进行比较,可得到相同的结论。

图3 开槽管型药柱燃烧过程中的三维视图Fig.3 Three-dimensional view of slotted tube grain in burning process
由开槽管型药柱总燃烧面积式(12),可得N=5、6、7时的燃烧规律,如图4所示。
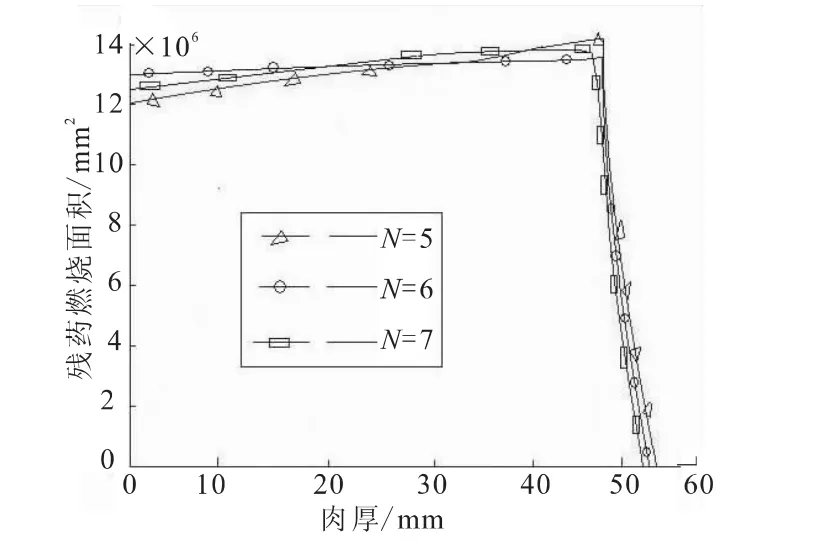
图4 燃烧规律曲线图Fig.4 Curves of the burning law
图4表明,相同的装药量下,开五槽时燃烧规律呈现增面性,且增面幅度较大;开六、七槽时呈现先增面性后减面性,且开六槽时增减幅度较小,接近恒面性,开七槽时增减幅度较大。与本文2.4节中所得燃烧规律相吻合。
表1为开六槽的管型药柱在e=0和e=e1两点时,利用UG软件提取燃烧面积与公式计算的燃烧面积数据的对比。由表1可知,公式计算的数据与实际数据的误差极小,证明了公式的正确性。

表1 数据对比Table 1 Data comparison mm2
4 结论
(1)设计参数存在临界域;当设计参数值在临界域外时,呈现单纯的增面性或减面性;当设计参数值在临界域内时,呈现先增面性后减面性;且设计参数值越接近临界域均值,燃烧规律越接近恒面性。
(2)经算例比较可知,对于开五、六、七槽的管型药柱,开六槽时燃烧规律最接近恒面性。
(3)开槽管型药柱燃烧规律不存在恒面性。
[1]王元有.固体火箭发动机设计[M].国防工业出版社,1984.
[2]夏志全.端面燃烧发动机研制中应注意的几个问题[J].固体火箭技术,2000,23(2):12-15.
[3]葛爱学,夏智勋,方丁酉.两种新型药型的燃面规律之比较[J].固体火箭技术,2000,23(3):7-10.
[4]Hawkins David K,Campbell Carol J.Advanced designs for high pressure,high performance solid propellant rocket motor[P].USP 6682615,2004.
[5]王春利,孙维申,邹广宝.开槽管型装药(减面形)的设计与应用研究[J].固体火箭技术,1996,19(3):41-45.
[6]魏志军,张平,方蜀州.美国“爱国者PAC-3”型导弹主发动机装药药型反设计[J].固体火箭技术,2004,27(2):114-116.
