飞行器系统参数变化对章动过程的影响分析①

刘平安，郜 冶，王 革

(哈尔滨工程大学航天工程系，哈尔滨 150001)

0 引言

小卫星发射的最末级通常使用旋转固体火箭发动机作为动力装置，在旋转飞行器固体火箭发动机工作过程中，随着推进剂的燃烧，系统的质量逐渐减少，使得系统的质量特性与能量特性发生变化，最终导致了飞行器章动的增长［1－7］。为了深入理解章动过程中能量损失的作用效果，需对系统能量耗散过程进行研究。能量耗散是指物体在做回旋运动时的弹性振动所产生的效果。这种耗散会导致进动角θ产生一个偏离，且越来越大。一个轴对称的物体旋转时，遵守转动惯量守恒，如果没有这种弹性振动，就不会产生进动角的耗散作用。若不存在外部力矩，它将以恒定的姿态保持稳定的进动。若施加一个力矩，这个进动角就会增加，当力矩的作用停止，进动角的增加也随之停止，将保持一稳定值。

物体旋转时，如果没有能量耗散，转动惯量的最大轴和最小轴都是稳定的。当存在能量耗散时，只有转动惯量的最大轴是稳定的。这时，当物体围绕转动惯量最小轴旋转时，进动角将会继续增大，直到改变运动姿态，围绕转动惯量最大轴旋转。当飞行器的侧向转动惯量大于轴向转动惯量，对常用的细长体结构来说，是固有的、不稳定的。

本文从能量耗散的角度出发，研究飞行器系统参数变化对章动效果的影响。

1 控制方程

在没有外力矩作用的情况下，质量特性不变的弹性体做回旋运动时，欧拉动力学方程如下:

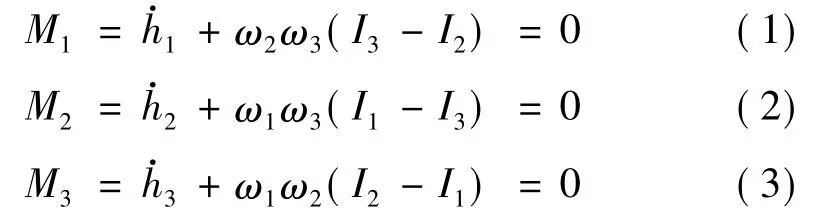
角动量矢量可表示为

旋转动能可表示为

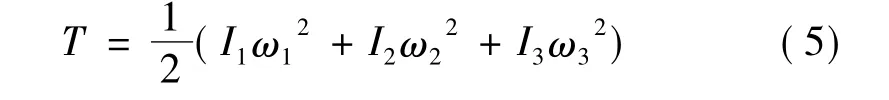
对于轴对称飞行器，记作I1=I2=I，角动量值的平方可表示为

转动动能可化简为

由式(6)、式(7)可得:

由于 H=Iω3/cosθ，式(8)可表示为

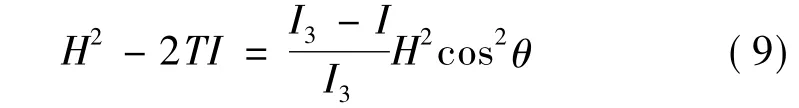
对旋转动能求时间的导数:

由式(10)可看出，章动角的变化率依赖于系统动能的变化率。随着系统动能的耗散，章动角的变化率可增可减，取决于转动惯量各分量的大小。对于实际的飞行器，由于推进剂的燃烧，伴随着燃气流的喷出，产生了喷气阻尼作用，系统的能量发生了变化，动能的变化率不再为零。由于质量的损失，产生了能量的耗散，章动角速率也会发生变化。由于系统经历了质量的减少及相应的喷气阻尼作用，欧拉动力学方程可表示如下:

在飞行器系统不受外力矩作用的情况下，3个方向的欧拉方程可表示为

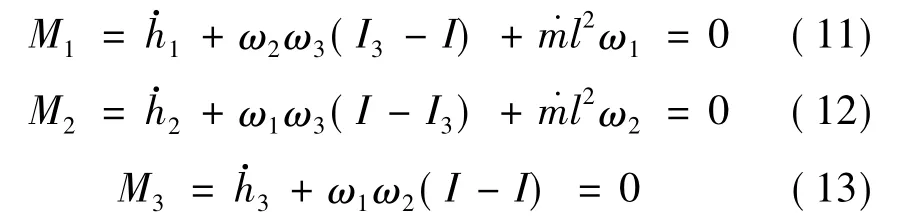
化简可得:

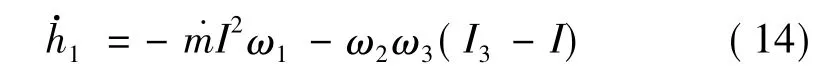
把角动量表达式带入方程(14)～(16)，写成角速度变化率的函数:

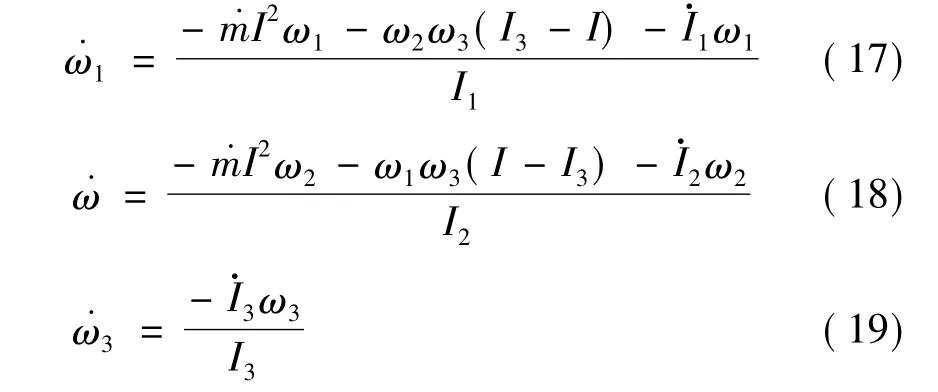
方程(17)～(19)是系统的角速度方程，描述了飞行器系统在质量减少、能量耗散过程中三向角速度的变化率。通过求解这3个方程，可得到章动变化过程中三向角速度的变化。

尽管章动角度发生了变化，在每一瞬时，角动量矢量与其分量在数值上保持相同的关系，即 H=Iω3/cosθ。这时，对式(9)进行求导，化简可得到飞行器系统的能量耗散方程:

从式(20)可看出，旋转飞行器系统，随着质量减少，引起了系统能量的耗散，章动角的变化率依赖于系统动能的变化率。

当考虑质量变化时，对系统的转动动能求导化简可求得章动角的变化率:

方程(21)是系统的章动方程，表达了在考虑旋转飞行器系统质量变化，及其带来的喷气阻尼作用的条件下系统章动角的变化率。通过求解方程(21)，可得到系统章动角随时间的变化历程，或增大或减小。

至此，推导了旋转飞行器工作过程中，伴随着固体推进剂的燃烧，飞行器总的质量减少，引起了系统能量的耗散，以及相应的角速度与章动角的变化，得到了飞行器系统的角速度方程与章动方程。通过方程(17)～(19)可求解三向角速度的变化，通过方程(21)可求解章动角的变化。

2 计算结果与分析

2.1 算例1与分析

针对WESTAR-V飞行器，求解其角速度方程与章动方程。采用文献［8］中的方法，在飞行器的工作过程中，将系统具体参数的变化，包括转动惯量、质量流量、平均燃烧室半径与质心位置(质心到喷管出口的距离)，根据实际数据用公式拟合成时间的函数。

侧向转动惯量:

轴向转动惯量:

平均燃烧室半径:

质心位置(质心到喷管出口的距离):

发动机的质量流量:

把这些参数代入角速度方程与章动方程，用四阶的龙格库塔法求解，计算结果见图1～图3。

图1 WESTAR-V俯仰角速度随时间的变化Fig.1 Chang of pitch angular rate of WESTAR-V

从图1和图2可知，WESTAR-V飞行器俯仰角速度与偏航角速度的相位相差90°。飞行器系统随着推进剂的燃烧，质量逐渐减少，引起了系统能量的耗散，使得系统的俯仰角速度与偏航角速度逐渐增加，到燃烧结束时达到最大值，在30°/s附近。实际飞行器系统的俯仰角速度与偏航角速度［9］的变化见图4和图5。可看出，由计算得到的结果与实际飞行器俯仰角速度与偏航角速度的变化规律一致，都呈现出了侧向角速度的增长。

图2 WESTAR-V偏航角速度随时间的变化Fig.2 Chang of yaw angular rate of WESTAR-V

图3 WESTAR-V章动角随时间的变化Fig.3 Chang of nutation angular rate of WESTAR-V

图4 WESTAR-V飞行器俯仰角速度随时间的变化Fig.4 Chang of pitch angular rate of WESTAR-V spacecraft

从图3可知，WESTAR-V飞行器的章动角以近似指数的形式增加，从初始的0.9°增加到燃烧结束时刻的17°，这与实际的飞行器数据一致［9］。章动角的迅速增大是飞行器系统由于质量变化引起能量耗散的结果。

从算例1可知，从飞行器系统质量变化引起能量耗散的角度出发，推导得到的角速度方程与章动方程，可正确描述飞行器旋转章动过程中的角速度变化与章动角变化趋势。计算结果与实际数据趋势的一致性也说明了所采用的计算方法是可信的。可使用该方法计算具有旋转章动不稳定性的飞行器的参数变化，研究飞行器其他参数变化对飞行器系统角速度变化与章动角变化的影响。

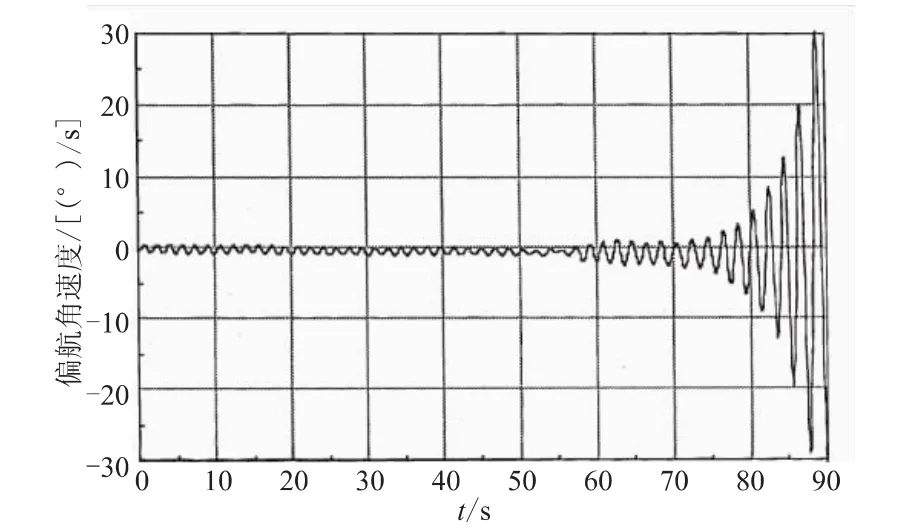
图5 WESTAR-V飞行器偏航角速度随时间的变化Fig.5 Chang of yaw angular rate of WESTAR-V spacecraft

2.2 算例2与结果分析

改变WESTA-V飞行器的参数，考察参数变化对飞行器章动过程的影响。首先，考察发动机质量流量的变化对飞行器章动过程的影响，保持其他参数不变，将质量流量减小、增大，求解章动角与侧向角速度。其中，减小的质量流量为˙m1=15.331+0.045 1 t，增大的质量流量为˙m2=24.095+0.045 1 t。

当质量流量减小时，俯仰角速度的变化如图6所示，偏航角速度的变化如图7所示，俯仰角速度与偏航角速度在燃烧结束时达到最大，在18°/s左右，两者的相位相差90°。与 WESTAR-V飞行器相比(30°/s左右)，侧向角速度明显降低。章动角的变化如图8所示，从初始的0.9°增加到燃烧结束时刻的 15.5°，小于WESTAR-V飞行器的最大章动角(17°)。可见，当质量流量减小时，使得飞行器的侧向角速度的变化幅值减小，最大章动角减小，从而削弱了飞行器的章动效果。

当质量流量增大时，俯仰角速度的变化如图9所示，偏航角速度的变化如图10所示。俯仰角速度与偏航角速度在到燃烧结束时达到58°/s左右，两者的相位相差 90°。与 WESTAR-V飞行器相比(30°/s左右)，侧向角速度明显增大。

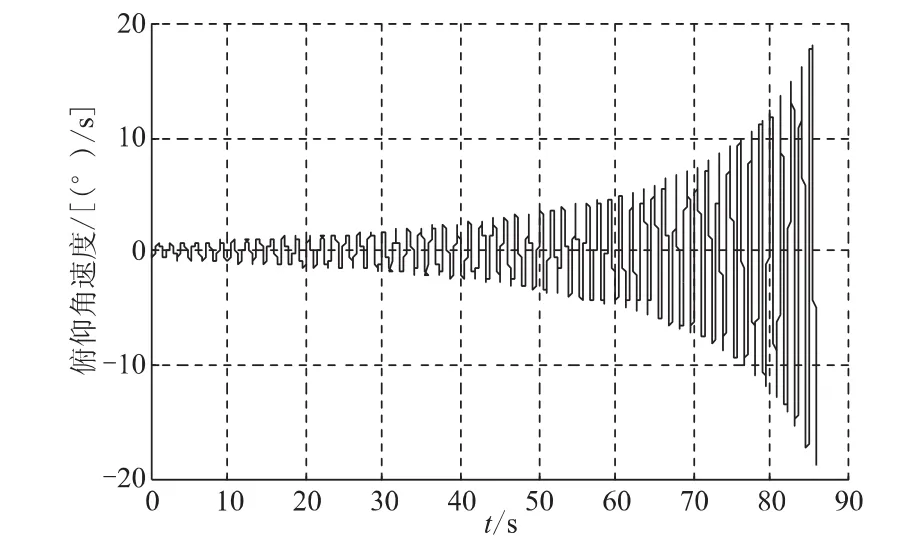
图6 质量流量减小时的俯仰角速度Fig.6 Pitch angular with mass rate decreasing

图7 质量流量减小时的偏航角速度Fig.7 Yaw angular with mass rate decreasing

图8 质量流量减小时的章动角Fig.8 Nutaion angular with mass rate decreasing

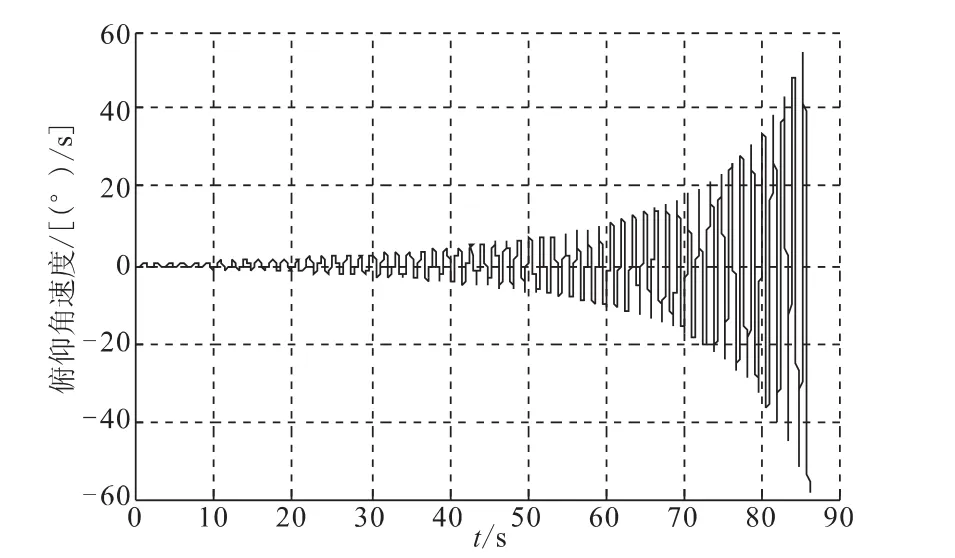
图9 质量流量增大时的俯仰角速度Fig.9 Pitch angular with mass rate increasing

图10 质量流量增大时的偏航角速度Fig.10 Yaw angular with mass rate increasing

章动角的变化如图11所示，从初始的0.9°增加到燃烧结束时刻的23.3°，明显大于WESTAR-V飞行器的最大章动角(17°)。可见，当质量流量增加时，使得飞行器的侧向角速度的变化幅值增大，章动角也大大增加，从而加强了飞行器的章动效果。

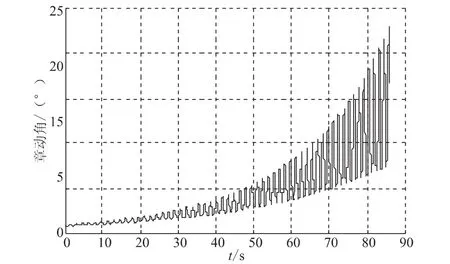
图11 质量流量增大时的章动角Fig.11 Nutation angular with mass rate increasing

从改变发动机的质量流量的计算结果可看出，发动机质量流量的变化在很大程度上影响了章动效果。随质量流量的增加，飞行器的章动效果明显加强。实际上，随飞行器型号的逐渐增大，必然采用更大尺寸的火箭发动机，以获得更大的推力，也就决定了发动机的质量流量随之增加。在STAR-48发动机之前，采用小型号的发动机STAR-37，由于推力小，质量流量小，并没有发生明显的章动放大行为。在STAR-48发动机之后，采用尺寸更大的发动机STAR-63，由于推力增加，质量流量增加，发生了更加严重的章动放大行为。这就从侧面印证了随发动机质量流量的增加，会增加飞行器的章动效果。

考察质心位置的变化对飞行器章动效果的影响，保持其他参数不变，将质心位置减小与增大，求解章动角与侧向角速度。lcg1是增大的质心位置，lcg2是减小的质心位置，lcg则是ESTAR-V飞行器实际的质心位置。其中:

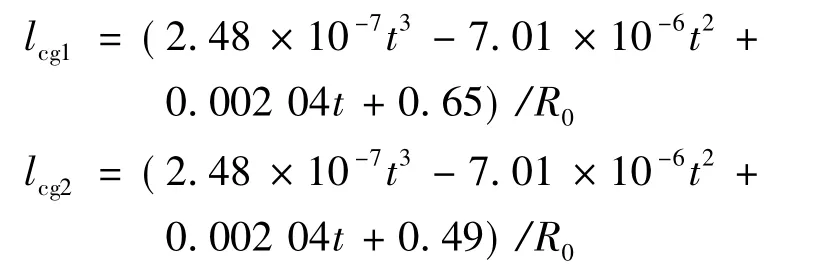
当质心位置减小时，俯仰角速度的变化如图12所示，偏航角速度的变化如图13所示。俯仰角速度与偏航角速度在燃烧结束时达到16°/s左右，与WESTARV飞行器相比(30°/s左右)，侧向角速度明显降低。章动角的变化如图14所示，章动角从初始的0.9°增加到燃烧结束时刻的15.1°，小于WESTAR-V飞行器的最大章动角(17°)。可见，当质心位置减小，使得飞行器的侧向角速度的变化幅值减小，最大章动角减小，从而削弱了飞行器的章动效果。

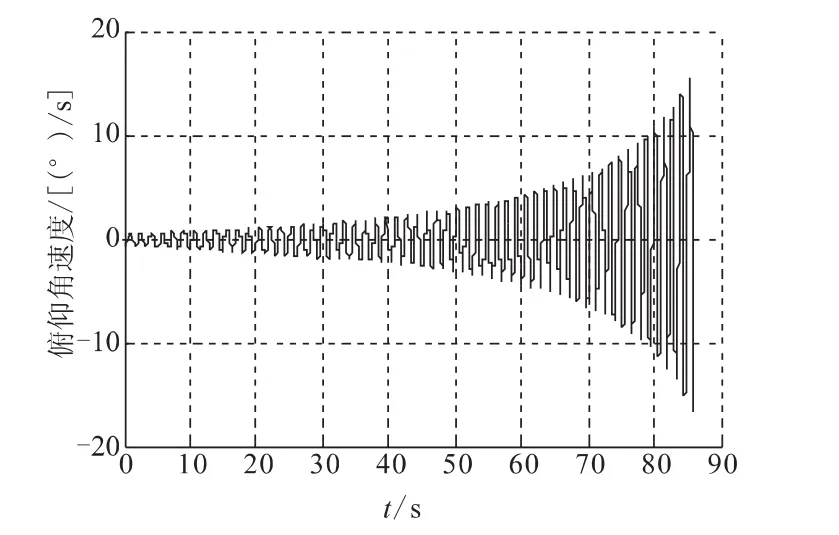
图12 质心位置减小的俯仰角速度Fig.12 Pitch angular with centroid position decreasing

图13 质心位置减小的偏航角速度Fig.13 Yaw angular with centroid position decreasing

图14 质心位置减小的章动角Fig.14 Nutation angular with centroid position decreasing

当质心位置增大时，俯仰角速度的变化如图15所示，偏航角速度的变化如图16所示。俯仰角速度与偏航角速度在燃烧结束时达到59°/s左右，与WESTARV飞行器相比(30°/s左右)，侧向角速度明显增大。章动角的变化如图17所示，从初始的0.9°增加到燃烧结束时刻的23°，明显大于WESTAR-V飞行器的最大章动角(17°)。可见，当质心位置增大，使得飞行器的侧向角速度的变化幅值增大，章动角也大大增加，从而加强了飞行器的章动效果。

从改变飞行器质心位置的计算结果可看出，飞行器质心位置的变化与发动机质量流量的变化一样，在很大程度上影响了章动效果。随质心位置的增大，飞行器的章动效果明显加强。从角速度方程(17)、(18)可看出，侧向角速度的变化率是受喷气阻尼项的影响。随发动机质量流量与质心位置的增大，喷气阻尼项也逐渐加大，对侧向角速度变化率的影响也会加大。由计算结果可知，当发动机质量流量与质心位置增大，侧向角速度随之增大，相应的章动角也随之增大，章动效果加强。可看出，喷气阻尼项对飞行器的章动过程起到了驱动作用，而不是阻尼作用。或者说，喷气阻尼项对章动过程所起的驱动作用超过了其所起的阻尼作用，最终表现为驱动作用，而不是文献中提到的阻尼作用。

图15 质心位置增大的俯仰角速度Fig.15 Pitch angular with centroid position increasing

图16 质心位置增大的偏航角速度Fig.16 Yaw angular with centroid position increasing

图17 质心位置增大的章动角Fig.17 Nutation angular with centroid position increasing

当考察轴向转动惯量的变化对飞行器章动过程的影响时，保持其他参数不变，将轴向转动惯量减小、增大，求解章动角的变化。发现随轴向转动惯量由小到大变化，飞行器系统的章动角大幅度减小，章动效果明显削弱。可见，增大飞行器系统的轴向转动惯量，有利于抑制飞行器系统的章动。

当考察侧向转动惯量的变化对飞行器章动过程的影响时，保持其他参数不变，将侧向转动惯量增大、减小求解章动角的变化。发现随侧向转动惯量由小到大的变化，飞行器系统的章动角大幅度增加，章动效果明显加强。可见，若要抑制飞行器系统的章动，需减小飞行器系统的侧向转动惯量。

从算例2可知，飞行器系统的章动过程受系统轴向转动惯量、侧向转动惯量、质量流量与质心位置等参数变化的影响。通过改变这些参数的变化，可改变飞行器系统的章动效果。当增大飞行器系统轴向转动惯量，减小侧向转动惯量，减小质心位置，减小发动机质量流量，可削弱飞行器系统的章动效果;反之，可增强飞行器系统的章动效果。所以，在设计飞行器系统时，可通过设计飞行器系统的参数，如轴向转动惯量、侧向转动惯量、质量流量与质心位置等，以便减小、削弱潜在的可能发生的章动现象。

3 结论

在旋转飞行器工作过程中，伴随着固体推进剂的燃烧，从飞行器系统质量减少，引起的能量耗散出发，推导得到了飞行器系统的角速度方程与章动方程，并通过适当的方法求解。通过具体算例验证了所推导的角速度方程与章动方程，可正确描述飞行器旋转章动过程中的角速度变化与章动角变化。计算结果与实际数据趋势的一致性，也说明了所采用的计算方法是可信的。使用该方法计算具有旋转章动不稳定性的飞行器的参数变化，研究了飞行器其他参数变化对飞行器系统角速度变化与章动角变化的影响。发现飞行器系统的章动过程受系统轴向转动惯量、侧向转动惯量、质量流量与质心位置等参数变化的影响。通过改变这些参数的变化，可改变飞行器系统的章动效果。当增大飞行器系统轴向转动惯量，减小侧向转动惯量，减小质心位置，减小发动机质量流量，可削弱飞行器系统的章动效果;反之，可增强飞行器系统的章动效果。通过具体算例验证了上述观点，所得结论可为具有旋转章动不稳定性的飞行器系统参数设计提供指导。

［1］Janssens F.Jet damping and nutation growth during the burn of a solid rocket motor such as PAM-D［J］.ESA Journal，1988，12:273-288.

［2］Eke F O，Mao T C.On the dynamics of variable mass systems［J］.The International Journal of Mechanical Engineering Education，2002，30(2):123-137.

［3］Eke F O，Mao T C，Morris M J.Free attitude motions of a spinning body with substantial mass loss［J］.Journal of Applied Mechanics，2004(71):190-194.

［4］Jeerapa Sookgaew.Effects of substantial mass loss on the attitude motion of a spinning rocket［D］.University of California，2004:13-23.

［5］郜冶，杨丹，熊永亮.旋转飞行器固体火箭发动机引起的章动不稳定性分析［J］.宇航学报，2008，29(1):270-275.

［6］杨丹，郜冶，熊永亮.旋转固体火箭发动机随质量变化的姿态运动分析［J］.推进技术，2008，29(1):8-12.

［7］郜冶，刘平安，杨丹.旋转固体火箭发动机飞行器章动不稳定机理述评［J］.固体火箭技术，2011，34(1):14-18.

［8］Tina Morina Rice.Application of energy analysis to the problem of propulsion driven nutation instability of spin stabilized spacecraft［D］.The University of Tennessee，2006:18-36.

［9］Flandro G A.Characteristics of nutation instability in ULYSSES/PAM-S spin stabilized spacecraft［R］.CA 92647，1987:30.