北大保送试题与代数基本定理
2012-08-28江苏南京外国语学校李平龙特级教师
☉江苏南京外国语学校 李平龙(特级教师)
题目已知f(x)是二次函数,且a,f(a),f(f(a)),f(f(f(a)))构成正项等比数列,求证:f(a)=a.
证明:设f(a)=qa(q>0),则f(f(a))=q2a,即f(qa)=q2a;同理有f(q2a)=q3a.
设f(x)=mx2+nx+r(m≠0),则由

②-①,得ma2(q2-1)+na(q-1)=a(q2-q),即(q-1)[ma2(q+1)+na]=qa(q-1). ④
③-②,约去q后同理可得(q-1)[ma2(q+1)q+na]=qa(q-1).⑤
假设q≠1,那么由④⑤两式,得ma2(q+1)+na=qa,且ma2(q+1)q+na=qa.
所以ma2(q+1)+na=ma2(q+1)q+na,即ma2(q+1)=ma2(q+1)q,ma2(q+1)(q-1)=0.因为m≠0,a≠0,q≠1,所以q+1=0⇒q=-1,这与q>0矛盾.
综上所述,q=1,即f(a)=a.
笔者经研究发现可做如下的类比、拓展与推广.
类比已知f(x)是二次函数,且a,f(a),f(f(a)),f(f(f(a)))构成等差数列,求证:(fa)=a.
证明:设f(a)=a+d,则f(f(a))=a+2d,即f(a+d)=a+2d;同理有f(a+2d)=a+3d.
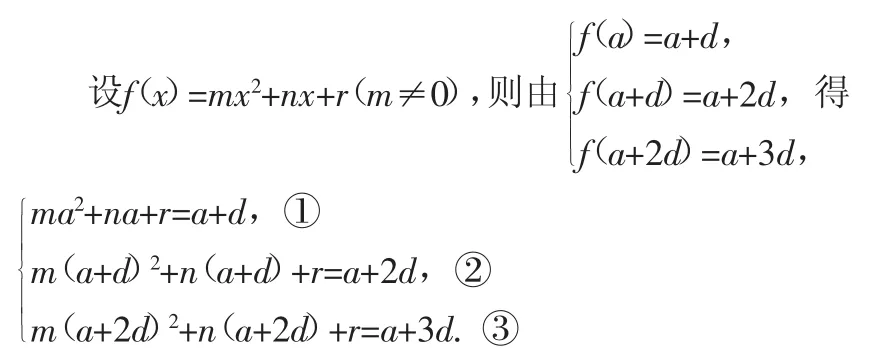
②-①,得md(2a+d)+nd=d,即d[m(2a+d)+n]=d. ④
③-②,同理可得d[m(2a+3d)+n]=d. ⑤
假设d≠0,那么由④⑤两式,得m(2a+d)+n=1,且m(2a+3d)+n=1,所以m(2a+d)+n=m(2a+3d)+n,即md=0,这与m≠0且d≠0矛盾.
综上所述,d=0,即f(a)=a.
拓展 已知(fx)是三次函数,且a,(fa),(f(fa)),(f(f(fa))),f(f(f(f(a))))构成正项等比数列,求证:f(a)=a.
证明:设f(a)=qa(q>0),则f(f(a))=q2a,即f(qa)=q2a;同理有f(q2a)=q3a,f(q3a)=q4a.
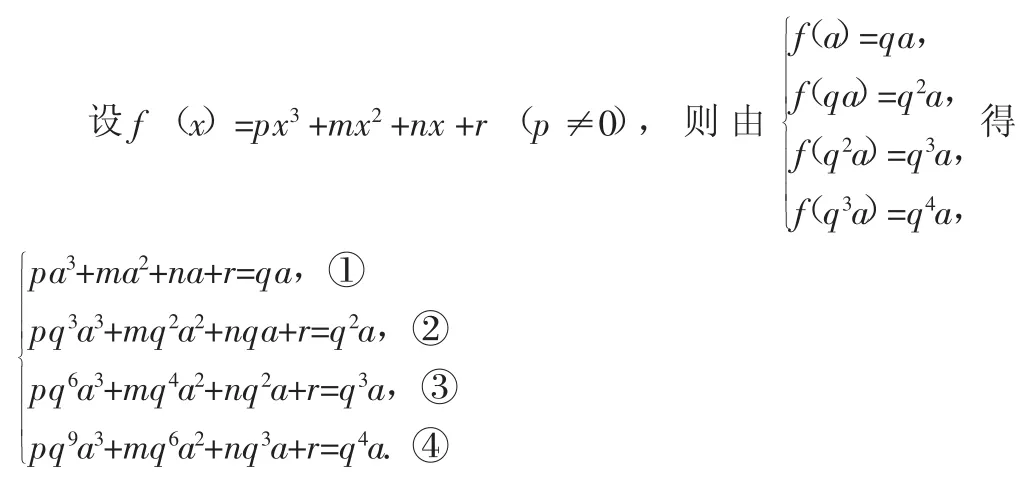
②-①,得pa3(q3-1)+ma2(q2-1)+na(q-1)=a(q2-q),约去a,即得(q-1)[pa2(q2+q+1)+ma(q+1)+n]=q(q-1).⑤
③-②,并约去aq可得:
(q-1)[pa2q2(q2+q+1)+maq(q+1)+n]=q(q-1).⑥
④-③,并约去aq2可得:
(q-1)[pa2q4(q2+q+1)+maq2(q+1)+n]=q(q-1).⑦
假设q≠1,那么由⑤⑥⑦三式,得:
pa2(q2+q+1)+ma(q+1)+n=q;
pa2q2(q2+q+1)+maq(q+1)+n=q;
pa2q4(q2+q+1)+maq2(q+1)+n=q.
以上三式说明,存在二次函数g(x)=p(q2+q+1)x2+m(q+1)x+(n-q),使g(a)=g(aq)=g(aq2)=0,即二次函数g(x)有三个零点,这是不可能的.
综上所述,q=1,即f(a)=a.
推广一般地,已知f(x)是一元n次多项式函数(n∈N*),且a,f(a),f(f(a)),f(f(f(a))),…,f(f(f(…f(a))))(共n+1个f)构成正项等比数列,求证:f(a)=a.
证明:设f(a)=qa(q>0),则f(f(a))=q2a,即f(qa)=q2a;同理有f(qk-1a)=qka,k=1、2、…、n+1.

综上所述,q=1,即f(a)=a.
