利用Radau伪谱法求解UCAV对地攻击轨迹研究

王 铀， 赵 辉， 惠百斌， 王 锋， 胡 杰

(1.空军工程大学航空航天工程学院，西安 710038; 2.中国人民解放军95737部队，重庆 402361;3.中国人民解放军94857部队，安徽 芜湖 241007)

0 引言

当无人作战飞机采用人工控制攻击方式时，由于通信链路存在固有延迟，并可能在复杂电磁环境下受到干扰，因此，攻击的可靠性和及时性受到严重影响。未来信息化条件下使用无人机进行空中作战时，无人作战飞机(UCAV)一旦确定攻击目标之后，应该根据当前的飞行条件、作战环境等诸多因素自主确定作战过程，自动解算发射诸元及发射轨迹控制，实施自主攻击作战。这样，可以有效地避免由于人为参与作战过程造成作战时机延误和差错，充分发挥无人机作战的主要特点和优势。因此，研究无人作战飞机自主攻击技术，体现了未来无人作战飞机的发展方向。

轨迹规划技术是实现UCAV自主攻击的关键技术。目前，国内外对其进行了大量的研究，主要包括:人工势场法、路图法、智能计算方法、基于采样的规划方法、最优控制法等［1－4］。近几年来，伪谱方法在最优控制问题的数值解法方面［5］，特别是飞行器轨迹优化方面变得逐渐流行，并逐渐成为研究热点［1，6－9］。常见的伪谱方法包括:Chebshev伪谱法(CPM)、Legendre伪谱法(LPM)、Gauss伪谱法(GPM)以及Radau伪谱法(RPM)。Radau伪谱法因其具有简单的结构、较高的精度、指数性的收敛速度，以及在处理连续时间最优控制问题上具有优势等特点得到了快速发展。考虑UCAV对地攻击需要在满足各种复杂约束的基础上规划出一条连续并且可行的最优轨迹，采用Radau伪谱法来求解UCAV对地攻击轨迹。

1 Radau伪谱法的基本原理

RPM求解最优控制问题的基本思路为:将未知的状态变量和控制变量在一系列Legendre-Gauss-Radau(LGR)点(LGR 点为多项式 Pn－1(τ)+Pn(τ)的零点，其中，Pn(τ)为n阶Legendre多项式)上离散化，然后采用Lagrange插值多项式来逼近真实的状态变量与控制变量，再通过对状态变量求导来代替动力学微分方程。这样，连续系统最优控制问题被转化为受一系列代数约束的参数优化问题［9］。

1.1 最优控制问题的一般框架

考虑Mayer型性能指标函数的一般最优控制问题

式中:J为性能指标;X(t)∈Rn，为状态变量;U(t)∈Rm，为控制变量，为微分方程约束条件;C［X(t)，U(t)，t］∈Rs，为状态变量和控制变量的约束条件;φ［X(t0)，t0，X(tf)，tf］∈Rφ，为边界约束条件;t为时间。

1.2 Radau 伪谱法

最优控制问题的时间区间为t∈［t0，tf］，采用伪谱法需要将时间区间转换到τ∈［－1，+1］。将t∈［t0，tf］分成 K 个网格，且∀t∈［tk－1，tk］，k=1，…，K，t0＜ t1＜…＜tK=tf，做如下映射变换

容易推出

用RPM伪谱法处理连续最优控制问题时，需要在一系列的离散点上对状态变量进行全局插值多项式逼近。状态变量在第k个(k∈［1，…，K］)网格处可以近似表示为

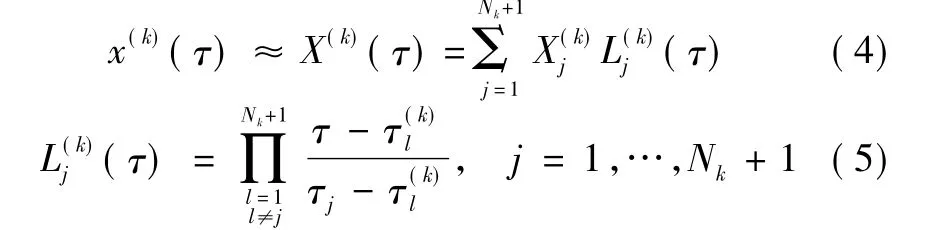
与状态变量不同的是，控制变量在1，…，K－1个网格处用如下的Nk阶Lagrange多项式来逼近

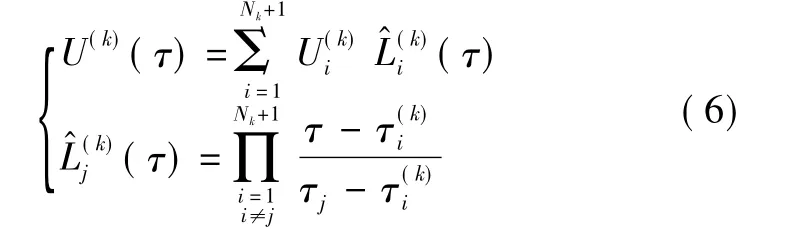
式中，k∈［1，…，K －1］。

因为终端时间tf没被配置，第K个网格的控制变量用如下的(Nk－1)阶Lagrange多项式近似表示为

式中，k=K。

性能指标函数可以近似表示为

将式(9)代入式(1)中动力学微分方程式，并在LGR点上进行离散，可得

式(1)中，不等式约束在第 k个(k∈［1，…，K］)网格用Nk个LGR点离散化处理，得

式(1)中，边界条件约束可以近似表示为

为保证网点的连续性，需满足下列条件

至此，连续系统最优控制问题被转化为受一系列代数约束的参数优化问题，可以采用非线性规划的方法进行求解。

2 空对地攻击轨迹规划问题数学建模

2.1 UCAV三自由度(3-DOF)质点模型

地理坐标系下，UCAV的质点运动学方程［10］为

航迹坐标系下，UCAV的质点动力学方程［10］为

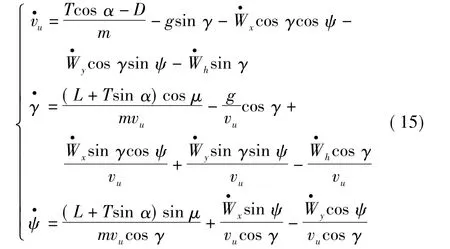
式(14)和式(15)中:(x，y，h)表示UCAV在地理坐标系中的经度、纬度和高度;vu为UCAV的真空速;γ、ψ、α、μ分别为航迹倾角、航向角、迎角、滚转角;m为UCAV的质量;g为重力加速度;T=δTmax，为发动机推力，δ∈［0，1］，为油门位置;Tmax为发动机最大可用推力;D=0.为阻力;，为升力;(Wx，Wy，Wz)和分别为风速和风力加速度沿坐标轴的分量。

2.2 UCAV 对地攻击的约束条件［1］

UCAV对地攻击时，需要满足的初始和终端位置、速度、姿态约束条件为

式(16)和式(17)分别为UCAV的初始和终端位置、速度、姿态约束，(xLAR，yLAR，hLAR)为攻击轨迹末端武器投放参考点坐标，Δx、Δy和Δh为给定的允许偏差;下标“f”表示轨迹末端点的状态。

UCAV在对地攻击过程中，要求时刻满足机动性能约束和环境约束条件，具体为

式中:X(t)=［x y h V γ ψ m］T∈R7，为状态变量;t∈［t0，tf］，终端时间tf自由。满足动力学微分方程约束(式(14)～式(15))

边界条件(式(16)～式(17)、式(21))

以及不等式约束(式(18)～式(20))

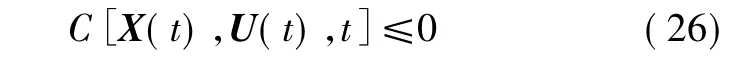
3 系统仿真

率;mmin为携带最小安全燃油量的飞行器重量;nmax为飞行器所能承受的最大法向过载。

战场环境通常包括地形、气象禁飞区和敌方火力或探测威胁。通常UCAV使用制导炸弹对地攻击是在中高空进行投放，因此本文不考虑撞地约束，仅讨论后两种约束。

气象禁飞区的约束条件式为

式中:‖·‖2表示两点之间的距离;(xNF，i，yNF，i)和 RNF，i分别为第i个气象禁飞区的中心坐标及半径。

敌方火力或探测威胁的约束条件式为

式中，(xNF，i，yNF，i，hNF，i)和 RT，i分别为第 i个威胁的中心坐标及作用半径。

此外，UCAV携带的武器还存在着使用约束(包括投放时法向过载约束和滚转角约束)，即

式中:nBomb_max和μBomb_min分别为投放时制导炸弹允许的最大法向过载和滚转角;tf为终端时间;nu=(L+Tsin α)/mg，为载机法向过载。

2.3 目标函数

对于对地攻击任务来说，一个重要的指标就是提升攻击的时效性，即最小化攻击时间，这对攻击时敏目标尤为重要。时间最小性能指标为

2.4 最优控制问题框架

至此，轨迹规划问题转化为最优控制问题:寻找控制变量 U(t)=［α μ δ］T，最小化迈耶尔(Mayer)型性能指标(式(22))为

为了验证文中所研究方法的有效性，对UCAV对地攻击轨迹规划过程进行仿真。仿真场景如下:UCAV从地理坐标系中(10，0，2)km点开始攻击，初始速度v0=210 m/s，航迹角 γ0=0°，航向角 ψ0=60°，总质量 m=17680 kg，特征面积 S=49.24 m2，武器投放参考点坐标为(15，30，6)km，终端速度 vf=300 m/s，航迹角 γf=0°，航向角ψf=35°，飞机性能参数参见文献［1］;由于实际作战中存在许多不确定因素，为了提高武器命中概率，一种较好的做法是尽量靠近可攻击区的中心。仿真中:武器投放参考点允许偏差为Δx=0、Δy=0、Δh=0;目标区中部署两个地方火力威胁AA及一个气象禁飞区WNF。具体见图1。

仿真在PC机上进行，CPU为2.79 GHz，在Matlab环境下利用SNOPT软件包进行求解。算例求得的满足约束要求的最短时间为94.5156 s，运算时间为19.78 s，算法具有一定的实时性。从图1～图4中可以看出，生成的飞行轨迹比较平滑，不仅能灵活地避开威胁，而且能以规定的投放姿态和速度准确进入武器投放参考点(理论计算误差为零)，而一般的航迹规划只能满足位置要求，而不能满足终端速度、姿态要求。

图1 UCAV对地攻击最优攻击轨迹Fig.1 Optimal air-to-ground attack trajectory

图2 最优攻击轨迹的速度曲线Fig.2 Time histories of velocity in optimal attack trajectory

图3 最优攻击轨迹的航迹倾角曲线Fig.3 Time histories of flight-path angle in optimal attack trajectory

图4 最优攻击轨迹的航迹偏角曲线Fig.4 Time histories of heading angle in optimal attack trajectory

4 结束语

本文构建了考虑多种约束的UCAV对地攻击轨迹规划模型，提出了一种基于Radau伪谱法(RPM)的求解策略，并阐述了最优控制问题的一般框架，为这一类最优控制问题的求解思路提供了参考。仿真结果表明，该方法能以较高的精度和速度生成满足终端位置、速度、姿态要求，综合考虑飞机平台性能、燃油、气象、火力或探测威胁、制导武器可攻击区等各种复杂约束要求，连续并且真实可行的最优轨迹，对轨迹规划问题的工程应用具有一定意义。

［1］ 张煜，张万鹏，陈璟，等.基于Guass伪谱法的UCAV对地武器投放轨迹规划［J］.航空学报，2011，32(7):1240-1251.

［2］ 朱国涛，周树道，吕波，等.基于气象威胁的无人机航迹规划方法研究［J］.电光与控制，2011，18(6):26-30.

［3］ 刘新，周成平，丁明跃.无人机快速航迹规划算法［J］.华中科技大学学报，2011，39(4):45-48.

［4］ 倪天权，王建东，刘以安.交叉粒群算法在无人机航路规划中的应用［J］.系统工程与电子技术，2011，33(4):806-810.

［5］ HUNTINGTON G T，RAO A V.A comparison between global and local orthogonal collocation methods for solving optimal control problems［C］//IEEE Proceedings of the 2007 American Control Conference，New York，2007:1950-1957.

［6］ BENSON A，THORVALDSEN T，RAO V.Direct trajectory optimization and costate estimation via an orthogonal collocation method［J］.Journal of Guidance，Control and Dynamics，2006，29(6):1435-1440.

［7］ 沈振，胡钰，任章，等.一种新型RLV再入轨迹在线规划方法［J］.宇航学报，2011，32(8):1670-1675.

［8］ 雍恩米，陈磊，唐国金.飞行器轨迹优化数值方法综述［J］.宇航学报，2008，29(2):397-406.

［9］ DARBY C L，HAGER W W，RAO A V.Direct trajectory optimization using a variable low-order adaptive pseudospectral method［J］.Journal of Spacecraft and Rockets，2011，48(3):433-445.

［10］ WILLIAMS P.Three-dimensional aircraft terrain following via real-time optimal control［J］.IEEE Journal of Guidance，Control，and Dynamics，2007，30(4):1201-1205.