模糊自适应滤波方法在相对导航系统中的应用

王艳东， 韩智华， 蔡君亮， 陈晓强， 吉庆昌

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

0 引言

相对导航是无人机利用其导航测量设备在一定条件下实时地确定编队飞行中无人机之间的相对运动参数。通常采用GPS/SINS组合相对导航［1］，应用卡尔曼滤波方法最优地估计出导航系统的误差状态，再用误差状态的最优估计值校正系统。但是，有时系统的状态方程是时变的，而且状态转移矩阵中含有导航信息及惯性元件测量值，这些含有误差的参数使得滤波器模型不准确。另外，系统噪声与观测噪声的统计特性等很难精确地估计或测定，所以采用常规卡尔曼滤波器时常常会发散［2］。为了解决此问题，通常采用自适应滤波技术，在进行滤波的同时，利用观测数据带来的信息，不断地在线估计和修正模型参数、噪声统计特性和状态增益矩阵，以提高滤波精度，得到系统状态的最优估计值。在以往的文献中通常只是对系统噪声与观测噪声方差阵进行调整，如果系统的状态方程不准确就会使滤波器发散，则不能满足滤波要求。

针对上述问题，本文采用一种新的模糊自适应卡尔曼滤波技术，即调整系统噪声与观测噪声的方差阵或强跟踪滤波方法进行自适应的滤波方法，与以往文献的方法相比，本文结合了两种滤波方法的优点，逐步调整系统中的参数，保证滤波器能实时处理新的量测值，以解决系统噪声和观测噪声不准确或是滤波器的发散问题。

1 相对导航模型系统模型

采用四元数作为相对导航系统状态变量，因为应用四元数法时，四元数姿态矩阵微分方程式只需要解4个一阶微分方程式组就可以了［3］，比计算方向余弦姿态需要更少的时间和较小的传递误差。

1.1 相对导航系统状态方程

相对导航系统状态变量为 X=［δP，δV，δq，δw，δf］T。其中:δP、δV 分别为地球坐标系下的位置、速度误差;δq为姿态角对应的四元数误差;δw、δf分别为陀螺仪和加速度计的输出值［4］。

假定单个无人机系统的状态方程为

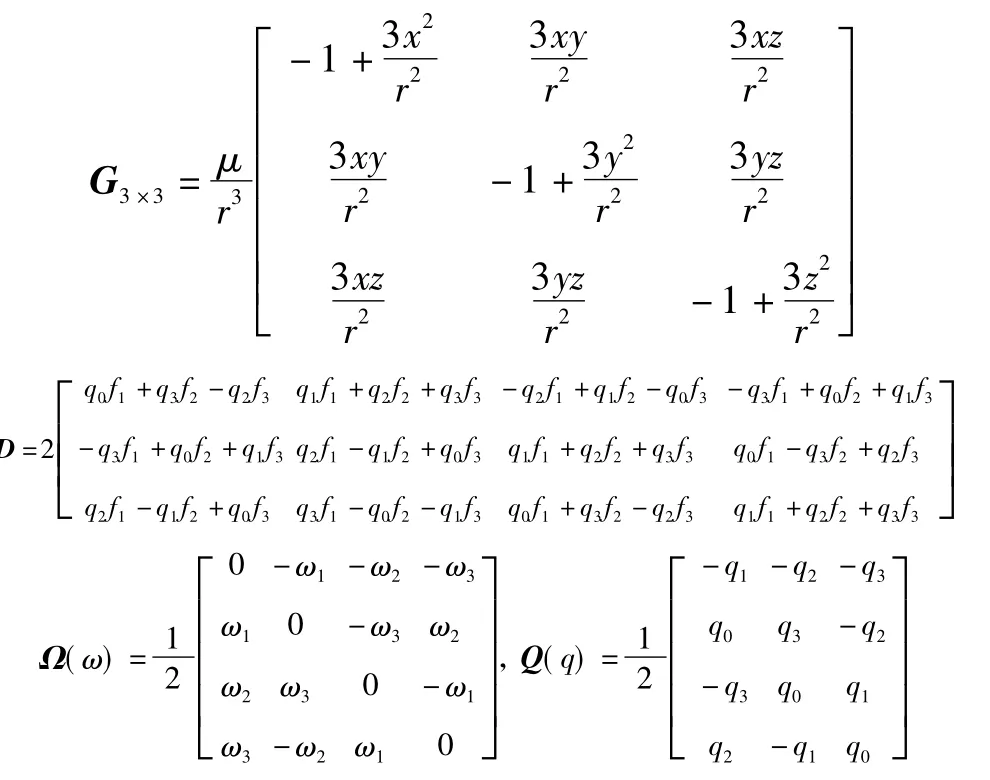
引导机和跟随机合并得到两无人机导航状态方程为

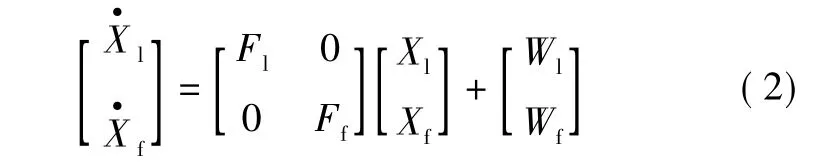
其中:下标l为引导机;f为跟随机。

式(2)经过转换得到两无人机的相对状态方程为

其中:ΔX=Xl－ Xf;ΔF=Fl－ Ff;ΔW=Wl－ Wf。

1.2 相对导航系统观测方程

定义相对导航系统的观测输出值为Z=［PINSPGPS，VINS－ VGPS］T。PINS、VINS分别为无人机 INS 输出的地球系下的位置、速度矢量;PGPS、VGPS分别为无人机GPS输出的地球系下的位置、速度矢量。

单个无人机系统的观测模型为

引导机和跟随机结合得到两无人机导航测量方程为

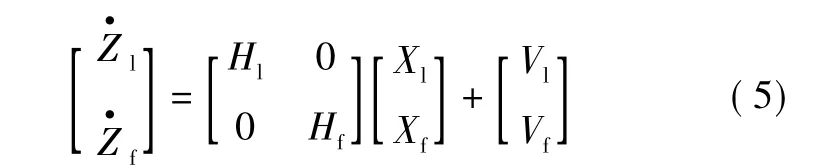
引导机和跟跟机相减得到两无人机的相对测量方程为

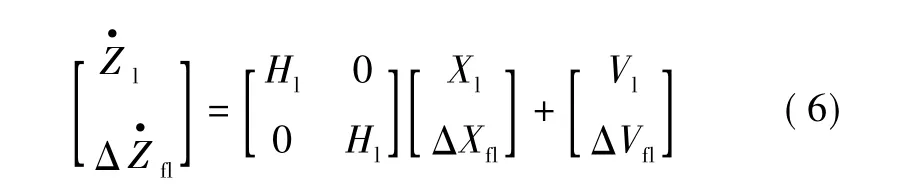
其中:ΔZ=Zl－ Zf;ΔV=Vl－ Vf。

2 模糊自适应滤波

对于INS/GPS组合导航系统，一般的线性离散系统数学模型［5－6］如下:

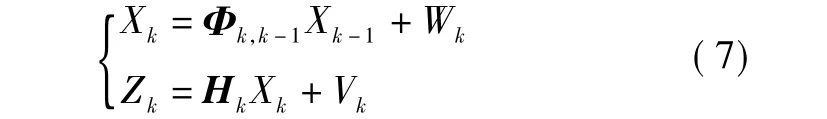
其中:Wk～N(0，Q);Vk～N(0，R)。

文献［7］给出了常规卡尔曼滤波的算法为

定义测量残差值(新息)

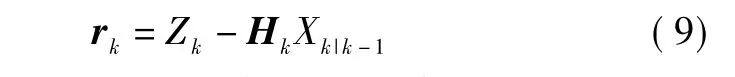
从式(8)可以看出，预测状态协方差阵Pk|k－1和量测噪声方差阵Rk的变化都能影响Kk的大小，从而改变滤波方程中新息的权重，影响新息在滤波中的作用。具体选用哪种方法，可见下面的判断不等式。

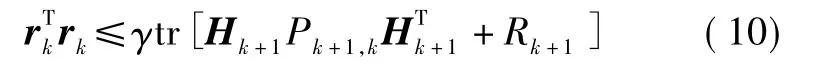
式中，γ为参数变量，一般按系统模型选取;tr表示求矩阵的迹。如果已知系统噪声与观测噪声而系统状态方程不准确，不等式(10)成立，选用强跟踪滤波;如果系统噪声和观测噪声未知，不满足不等式(10)，则选择调整Q和R。

下面逐一对两种方法进行分析。

2.1 调整系统噪声与观测噪声方差阵

如果数学模型足够准确，则残差序列应为零均值的白噪声，残差方差实测值与经过卡尔曼滤波得到的残差方差的理论值的差值应在0附近。如果此差值长期偏离0，则说明量测噪声水平已经发生了变化，需要对Q和R调整，调整的准则是使此差值回到0附近［8－9］。根据上述想法，设计自适应卡尔曼滤波器。

定义残差方差的理论值为pr，

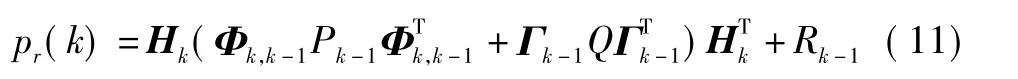
其中:cr为对最新的M各残差向量方差求平均值;i0=k－M+1，M为一经验参数，表示用来计算实际协方差阵的窗口大小，一般取20左右。

定义Qk、Rk分别为系统噪声方差阵和量测噪声方差阵变量:

式中:Q和R是初始常值;α、β是调整值，均为时变。根据Kalman滤波器的残差特性自适应地调整系统噪声和观测噪声误差方差阵，当α=β=1，就是常规的Kalman滤波。

定义残差实测方差与理论方差的差值为

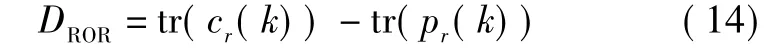
通过在滤波的每一采样点监控新息，得到均值和方差。根据式(7)，残差方差实测值与经过卡尔曼滤波得到的残差方差的理论值的差值应在0附近，均值也渐渐远离0点，则相应地做出调整:需改变Qk或Rk值，即若DROR＞0，则减小 Qk或Rk值;若DROR＜0，则增大Qk或Rk值。这样，滤波器增益矩阵也会相应减小，系统对量测值的信赖和利用程度减小，滤波性能趋于稳定。

2.2 强跟踪滤波方法

强跟踪滤波的初衷是为了使滤波器收敛，通过使用STKF降低精度来换取滤波的稳定性，即增大系统的噪声方差阵，这相当于将许多未建模的误差包含进来，使算法更简单可靠。

在式(8)中，系统的噪声方差阵Pk|k－1乘以一个系数λk

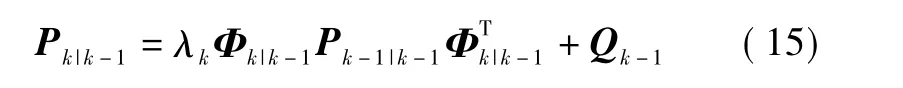
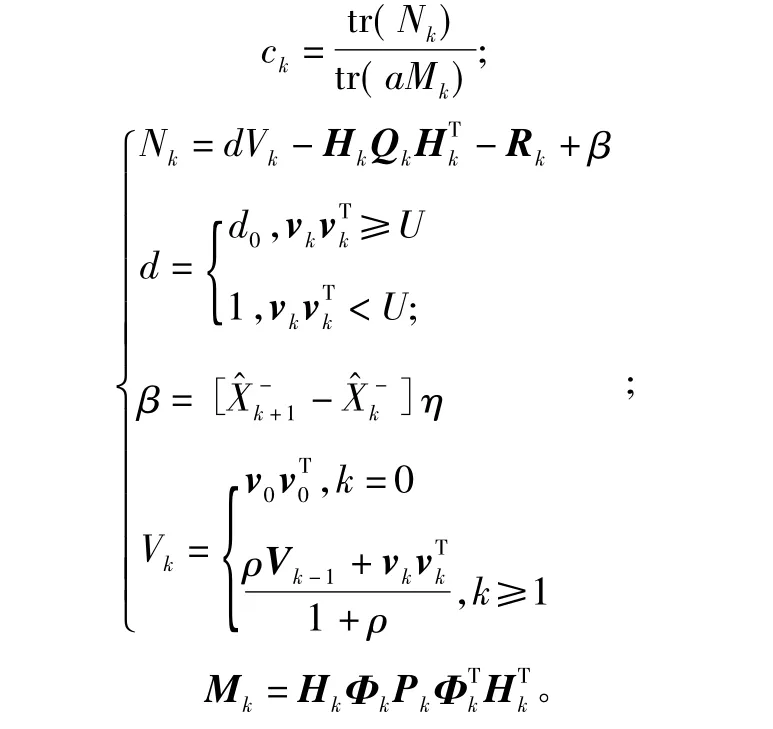
在STKF中关键的参数为λk，要得到λk还要求取4个参数 αi，ρ，d，β，其他参数通常根据经验获得，取 α1=α2=...=αm=1，0＜ρ≤1，d根据模糊自适应系统获取。

3 模糊自适应滤波实现

模糊推理原理如图1所示［10］。

图1 模糊原理图Fig.1 Schematic of fuzzy principle

图1 中，模糊化指将输入的物理量通过隶属度函数转换成模糊量;模糊推理指所有规则的前提条件与控制输入进行比较来确定哪一规则可用于当前的状态。匹配的过程包括每个规则应用的可能性。解模糊化指将模糊推理得到的模糊量转换为实际物理量。本文模糊推理系统(FIS)选择的类型为Mamdani，选择的模糊推理规则见表1。

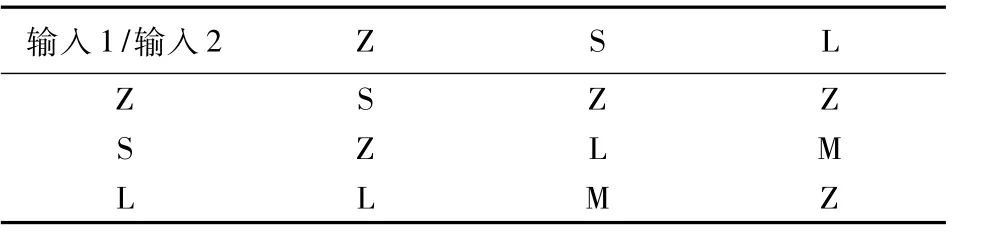
表1 模糊推理规则Table 1 Fuzzy inference rule

输入1为残差的实测均值，输入2为残差的实测方差与理论方差的差值DROR，输出则为α、β、d。解模糊化方法选用重心法，即输出取为隶属函数曲线围成区域面积的重心。采用形状为三角形的隶属度函数，速度和位置的输入输出隶属函数如图2所示。

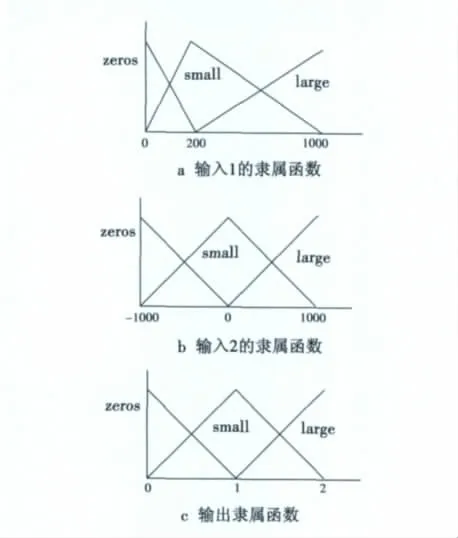
图2 输入输出隶属函数Fig.2 Input and output membership function

4 相对导航系统仿真

仿真通过Matlab和Fuzzy工具箱来实现。在基于模糊自适应卡尔曼滤波的系统仿真中，计算出每一采样时刻的滤波器的残差方差和均值，通过上述规则和方法，分别得到滤波器的系统噪声和量测噪声的调整值或是状态协方差阵，从而不断地修正滤波器，使滤波器趋于稳定，估计性能最优。

为了比较，在相同的条件下用标准卡尔曼滤波进行了仿真。表2是在其他条件相同的情况下分别改变Q和R的值，常规卡尔曼滤波和新自适应滤波(FLKF)的对比。

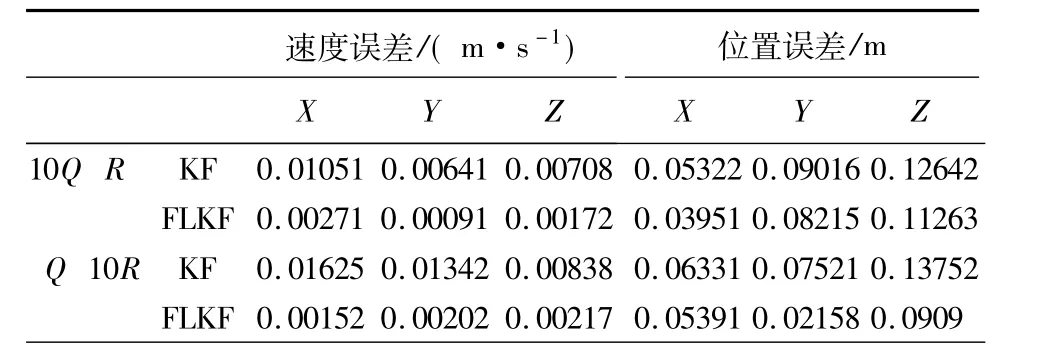
表2 FLKF和KF的比较Table 2 Comparison of KF and FAKF by changed Q/R

图3a、图3b分别是改变系统方程中的参数后得到的X轴、Y轴、Z轴方向相对位置误差和相对速度误差的仿真结果。图中，蓝线表示新自适应(FLKF)算法得到的结果，红线表示标准卡尔曼滤波算法(KF)得到的结果。

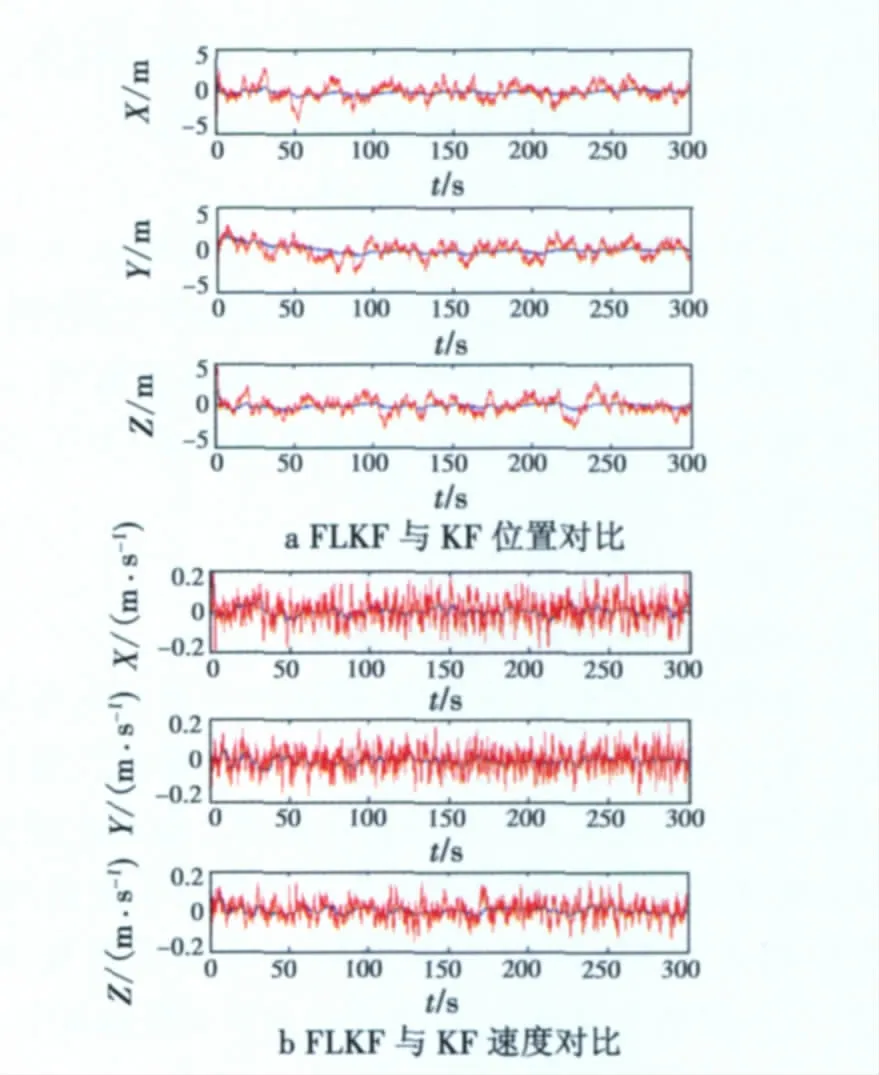
图3 FLKF与KF对比精度Fig.3 Comparison of KF and FAKF

从仿真结果来看，新的自适应滤波(FLKF)的误差均低于常规卡尔曼滤波器估计的误差，这说明采用此种自适应滤波(FLKF)的GPS/INS系统比用普通卡尔曼滤波技术具有更高的精度，模糊系统能适当降低卡尔曼滤波器的发散程度，从而达到了应用模糊自适应系统提高系统定位精度的目的。

但在仿真过程中由于要进行模糊系统运算，增加了判断语句和模糊算法，算法结构比较复杂，所以计算效率不高，在此可以进行一些简化。

当编队飞行中的两架无人机状态相似，两者之间相对线加速度和相对角速度较小时，可以假定:Ff≈Fl，对模型进行简化，代入全维滤波模型式(3)和式(6)后，可把相对导航系统状态模型降维为原来的一半，得到

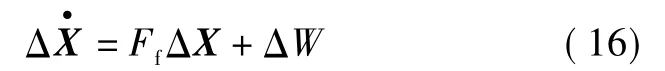
降维相对导航系统的观测方程为

进行计算仿真，由于模型维数减半，计算量下降，运算速度加快;但要求是两架无人机飞行状态相似，如果进行较大的机动飞行时，滤波的精度可能较差。

总结为:在无人机机动幅度不大、模型较为准确的情况下，采用降维滤波模型、常规卡尔曼滤波以节省定位时间;在无人机机动形式大、模型不准确的情况下，采用全维滤波模型、模糊自适应卡尔曼滤波来提高系统容错性。

5 结论

文章提出了一种新的模糊自适应滤波算法，并将其应用在INS/GPS相对导航系统中，同常规卡尔曼滤波算法进行了仿真比较，其算法简单，意义明确，收敛时间短，运算效率高;并且，它不受系统噪声方差和观测噪声方差改变的影响，对于系统模型不准确情况有较好的自适应效果。因此，它是一种较为理想的自适应滤波算法。

［1］ 徐俊，张珩.编队飞行GPS/INS相对导航的分布滤波算法［J］.电光与控制，2008，15(8):40－44.

［2］ 孟焱，孙增圻.INS/GPS组合导航中实时模糊自适应滤波技术的研究［J］.计算机工程与应用，2002，38(8):63－65.

［3］ FOSBURY A M，CRASSIDIS J L.Relative navigation of air vehicles ［J］.Journal of Guidance，Control，and Dynamics，2008，31(4):824－834.

［4］ 杨泗智.卫星组合导航与相对定位方法研究［D］.哈尔滨:哈尔滨工业大学，2006.

［5］ 徐田来，游文虎，崔平远.基于模糊自适应卡尔曼滤波的INS/GPS组合导航系统算法研究［J］.宇航学报，2005，26(9):571－575.

［6］ 柏菁，刘建业，袁信.模糊自适应卡尔曼滤波技术研究［J］.信息与控制，2002，31(6):193－197.

［7］ GENG Yanrui，CUI Zhongxing.Adaptive fading Kalman filter with applications in integrated navigation system［J］.Journal of Beijing University of Aeronautics and Astronautics，2004，30(5):434－437.

［8］ 徐光晨，翁泽宇，丁红钢，等.模糊自适应卡尔曼滤波在惯性/地磁导航中的应用［J］.舰船科学技术，2010，32(5):68－72.

［9］ 马忠孝，刘宗玉，陈明.基于模糊逻辑的自适应卡尔曼滤波在GPS/INS组合导航中的应用［J］.信息与控制，2006，35(8):457－461.

［10］ SASIADEKT J Z，WANG Q，ZEREMBA M B.Fuzzy adaptive Kalman filtering for INS/GPS［C］//Data Fusion Proceedings the 15th IEEE International Symposium on Intelligent Control.Rio，PatFas.GREECE，July，17－19，2000:181－l86.