海量目标量测数据下的目标跟踪

阮铖巍， 徐保伟， 寇英信， 李战武， 谷长春

(1.空军工程大学航空航天工程学院，西安 710038; 2.中国人民解放军95247部队，广东 惠州 516259)

0 引言

随着网络中心战的逐步实现，各种各样的传感器已经遍布陆、海、空、天等物理空间，以及电、磁等虚拟空间。例如，天基传感器依靠成像侦察卫星、电子侦察卫星、导弹预警侦察卫星、海洋侦察卫星等侦察卫星从太空轨道上对空中目标实施侦察、监视和跟踪;空基传感器系统依靠装载在轻型固定翼飞机、直升机、无人机以及高空系留气球上的雷达、光电设备、照相设备等对目标进行跟踪［1］;陆基传感器系统包括分布在陆地上的各种侦察设备，如雷达设备、电子侦听设备、激光、红外探测设备等［1］;海基传感器系统主要有水面舰艇和潜艇等平台携带的雷达、声纳、电子支援设备和光电设备等［2］。

由于现代战场中，各种各样的传感器广泛分布，对同一目标进行跟踪的传感器很多，会产生大量关于目标运动的数据。目前的跟踪算法对于这种大数据量的处理主要存在以下问题:1)当需要融合的数据量比较大时，各种滤波融合算法计算量较大，计算的实时性较差［3－4］;2)多传感器所获取的大量数据的管理比较复杂［5］;3)对于一般融合跟踪算法，都需要确切知道系统模型和量测模型［6－7］;4)在完成整个目标跟踪的任务中，可能会有部分传感器退出跟踪任务，而另一部分传感器加入跟踪任务。传感器的退出、加入更是增加了一般多传感器融合跟踪算法的实现难度。

如何从大量传感器对同一个目标进行跟踪时产生的海量目标量测数据中提取可用信息，同时避免不必要或者不可靠信息，最终估计出目标的运动状态，对于网络中心实现目标的跟踪来说是迫切需要解决的问题。

1 传感器模型

传感器对目标运动参数的测量一般是通过对目标定位的方式进行的，因此一般传感器的量测为目标当前时刻的位置。本文所研究的传感器为该类传感器。

对于传感器，除了关注所测量的量以外，一般还关注数据更新周期、量测数据的分布等信息。但是，对于大多数传感器，更新的周期并不固定，而且量测的误差大小也会变化。更新周期的变化意味着某一个传感器在有了一次量测之后，下一次量测的更新时刻就未知，量测误差也会随时间改变，即对于同一个传感器前后两次量测相互独立，没有相关性。为了避免这种情况影响滤波精度，同时也为了简化统计计算量，本文没有利用这些未定信息，只是利用了传感器的量测值，这意味着本文方法的普遍适用性。

传感器有两种最优工作状态:1)概率最优;2)期望最优。概率最优是指在量测过程中，量测值为真实值的概率最大，对于噪声也就是说，噪声为零的概率最大。期望最优是指在量测过程中，量测值的期望值为目标真实值，即噪声的期望值为零，即零均值噪声。本文假设传感器正常工作状态为期望最优，即量测噪声为零均值噪声。

基于以上分析，本文建立传感器模型。

1)周期服从一个有界均匀分布，即周期

这样可以保证传感器的周期是随机的。

2)实际量测中，传感器的周期是会变化的，因此传感器实际更新周期为由式(1)得出的周期加上一个随机误差

3)传感器噪声为零均值正态噪声分布，方差服从0～1000的均匀分布。

2 统计量测基础

2.1 相关定义及说明

定义1统计量测点。对于传感器海量的量测数据，通过统计计算出某时刻的目标位置点，该时刻称为统计时刻，该点称为统计量测点，如图1所示。

图1 统计量测点Fig.1 Statistical measuring points

定义2统计量测周期。统计量测点的更新周期。

定义3统计量测跨度。以统计时刻为结束时刻的一个时间段，统计量测点是通过在该时间段的实际传感器量测数据统计计算出来的。

显然，统计量测点并不是某一传感器实际量测值，而是众多传感器在统计时刻前一段时间(统计量测跨度)内的实际量测数据通过统计计算出来的“统计点”。

2.2 统计量测定理及证明

定理1设n个传感器同一时刻对同一目标的量测为X1，X2，…，Xn，量测之间相互独立，每一个传感器的噪声都为零均值噪声，即满足

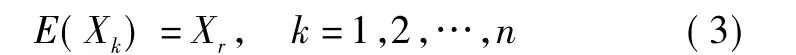
式中，Xr为目标真实量测，即其期望都为真实目标位置值。那么，当测量数据n足够大时，可用n个数的平均值来近似估计实际目标位置，并且统计量测点估计方差也可得出。

1)统计量测目标估计位置为

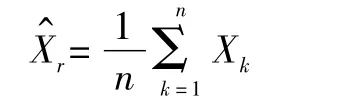
2)统计量测点估计方差为

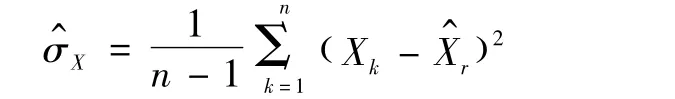
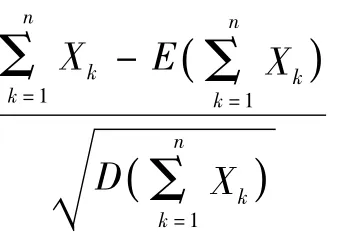
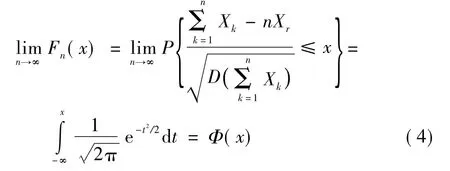
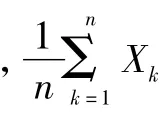
3 海量量测数据下的目标融合跟踪算法

3.1 统计量测跨度中的实际量测点外推

由于统计时刻是在统计量测跨度时间段的结束点，而实际量测数据的时刻不一定是该时刻，所以，计算统计量测点前应该将统计量测跨度中的实际量测点外推至统计时刻。

为了减少滤波外推对于大机动目标运动预测的误差，选用一个比较好的模型算法非常重要。本文选择文献［10］中改进的交互式当前统计模型算法进行滤波。

设系统状态向量为

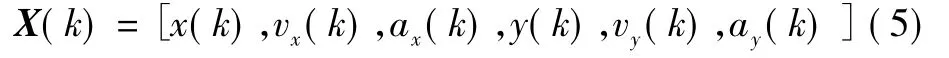
系统的状态方程为

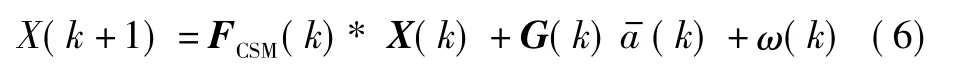
式中:FCSM(k)为目标状态转移矩阵;G(k)为输入控制矩阵;为机动加速度的均值。具体矩阵形式参见文献［10］。过程噪声ω(k)的协方差

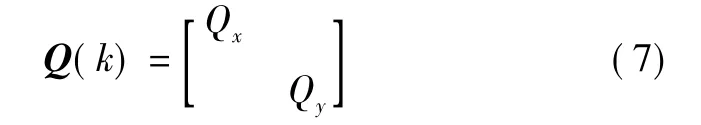
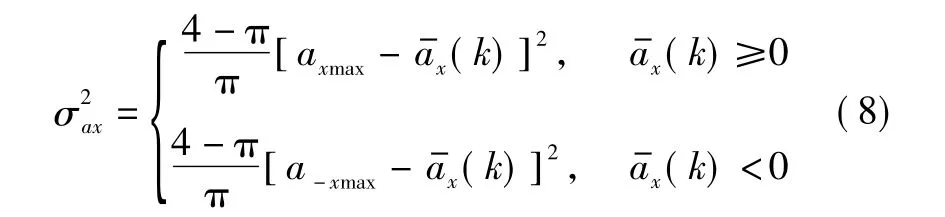
式中:axmax和a－xmax分别为x方向上的最大正、负加速度;Q的取值参见文献［11］。同样，Qy也可用此方法求出。

3.2 统计量测IMM滤波

1)初始化。

设有N个模型，每个模型给定一个典型机动频率和最大正负加速度以及模型间的转移概率ΠN×N，并设第k+1个统计量测跨度时间段内有n个实际测量数据。

2)模型输入交互。

交互模型i的状态估计和状态协方差阵

3)实际量测点外推。

外推时间大小为量测数据更新时刻到统计时刻的时间段长度。为了简化计算，提高计算速率，外推时的状态直接近似为前一统计量测点的滤波状态。

设第k+1个统计量测跨度时间段内第p个实际测量数据更新时刻为Tk+1，p，并设统计量测周期为Tr，则该实际量测点的外推时间 ΔTk+1，p=p·Tr－ Tk+1，p。

然后，通过预测方程

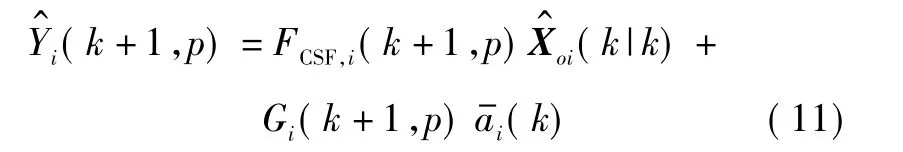
即可进行由实际量测数据更新时刻到统计时刻的外推。

有了第i个模型的外推预测状态，通过输出交互即可得到第k+1个统计量测跨度内的第p个实际量测的外推状态

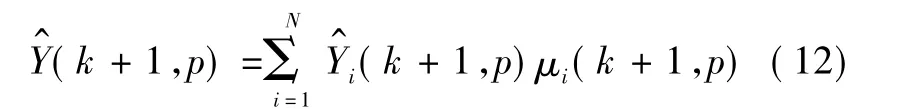
4)统计量测计算。

根据统计量测定理，统计量测点数据计算如下

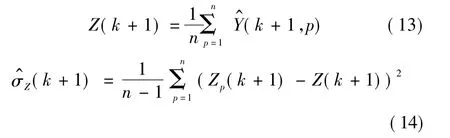
5)滤波。

一步预测得

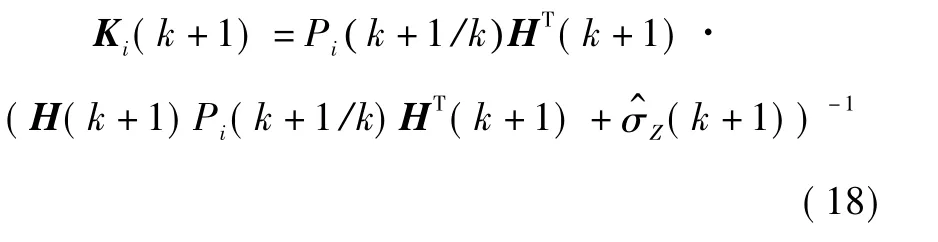
滤波增益

状态估计

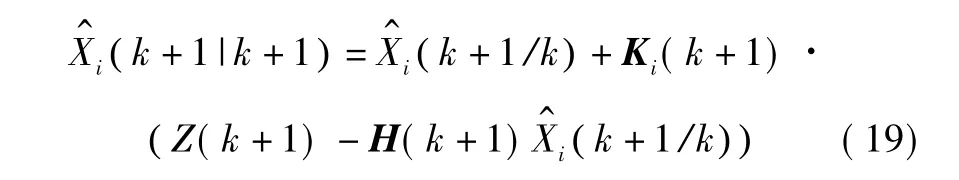
协方差估计

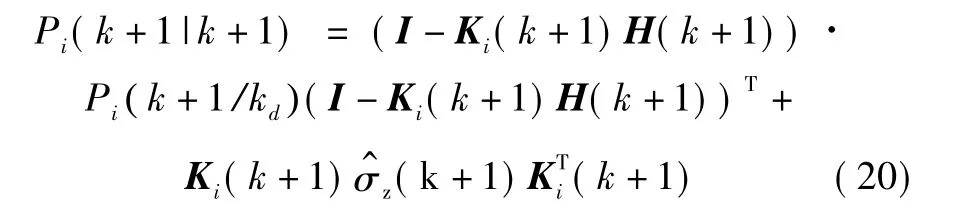
6)模型i概率更新。

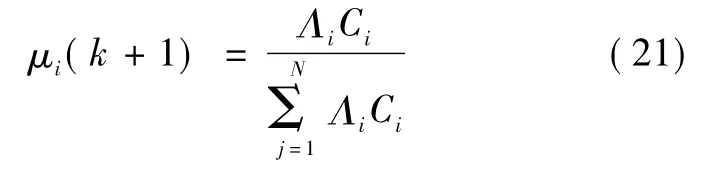
其中

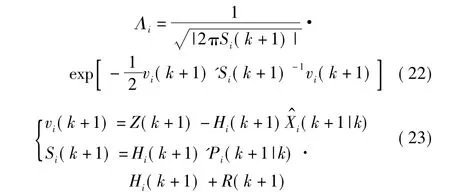
式中:vi(k+1)为新时刻新息;Si(k+1)为新息协方差。

7)输出交互。

4 仿真结果与分析

假设目标起始位置为(0 m，1000 m)，目标速度为300 m/s，水平指向x轴方向，目标运动规律如表1所示，运动轨迹如图2所示。图2中小圆为目标起始位置，小三角为目标运动终止位置。

表1 目标真实运动方式Table 1 The target's real movement mode

本文假设量测传感器数目为40个，每个传感器更新周期在0.01～2 s内均匀分布，即更新周期

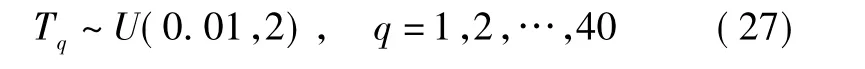
根据以上假设，并根据传感器模型最终得到实际量测点如图3所示。

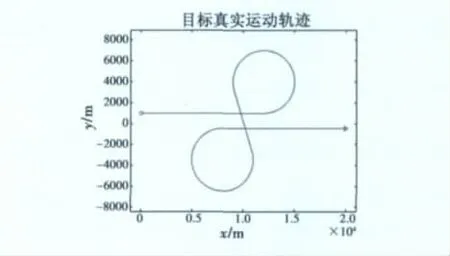
图2 目标运动轨迹Fig.2 The target’s track

仿真中，取统计量测周期为1 s，统计量测跨度也为1 s。基于以上假设，在选择合理滤波参数的情况下，应用本文提出的统计滤波方法，得出各统计量测点及最终滤波结果如图4～图6所示。

从图4和图5可以看出，海量的量测数据经过本文统计方法进行估计预测后，在大大减少数据处理难度的基础上，也能够达到令人满意的跟踪效果。特别是在目标没有做机动运动的情况下(90～110 s和160～200 s)，跟踪误差几乎为零。在目标做大机动时，跟踪位置误差也在200 m范围内。

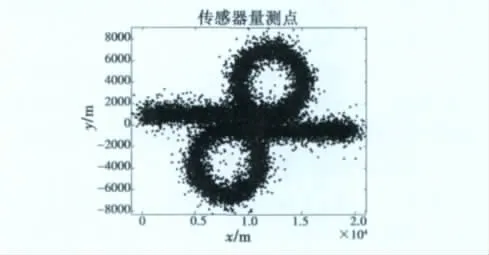
图3 实际量测点Fig.3 The actual measuring points

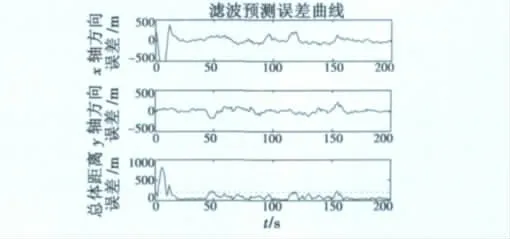
图4 目标位置误差Fig.4 The error of target position

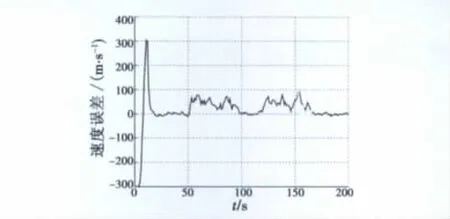
图5 目标速度误差Fig.5 The error of target velocity

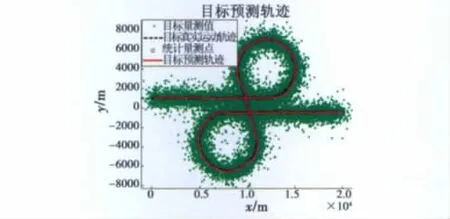
图6 目标预测轨迹Fig.6 Computed track of the target

5 小结

针对现有跟踪算法对于海量量测数据处理的困难，提出了本文统计量测的方法。仿真验证了该方法的有效性。但是，值得注意的是关于统计方法中统计量测间隔和统计量测周期的选取问题。统计量测间隔短，统计的量测数据量就小，可能就会超出中心极限定理的适用范围;统计量测周期取太小，则会出现部分量测数据重复利用，增加计算量;统计量测间隔太长或者统计量测周期取太大的话，当目标做大机动时就会出现“跟不上”的情况。

［1］ 张冬辰，周吉，吴巍，等.军事通信:信息化战争的神经系统［M］.北京:国防工业出版社，2008.

［2］ 陈克伟，赵滨江.论网络中心战［M］.北京:解放军出版社，2004.

［3］ DOGANCAY K，TANRIKULU O.Adaptive filtering algorithms with selective partial updates［J］.Analog and Digital signal processing，IEEE Transactions on，2001，48(8):726－729.

［4］ KARLSSON R，SCHO¨N T，GUSTAFSSON F.Complexity analysis of the marginalized particle filter［J］.Signal Processing，IEEE Transaction on，2005，53(11):4408－4411.

［5］ 周傲英，金澈清，王国仁，等.不确定性数据管理技术研究综述［J］.计算机学报，2009，32(1):1－16.

［6］ 何友，王国宏，关欣，等.信息融合理论及应用［M］.北京:电子工业出版社，2010.

［7］ 何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.2版.北京:电子工业出版社，2009.

［8］ GILLISPIE C C.Dictionary of scientific biography［M］.New York:Charles Scribners Sons，1971.

［9］ 董晴.独立随机变量的中心极限定理［J］.重庆工学院学报:自然科学版，2007，21(7):85－88.

［10］ 谭顺成，王国宏，王娜，等.改进的交互式当前统计模型算法［J］.电光与控制，2011，18(4):21－25.

［11］ 周宏仁，敬忠良，王培德，等.机动目标跟踪［M］.北京:国防工业出版社，1991.