举一反三，一题多解

☉河南濮阳市四中 刘建营

数学是一门培养思维的学科，我们学习数学时要能够举一反三，有时对一道题深入研究，尝试用不同的解法来解，可以开发学生的智力，提高学生的发散思维能力，培养学生的创新精神.下面举例分析.

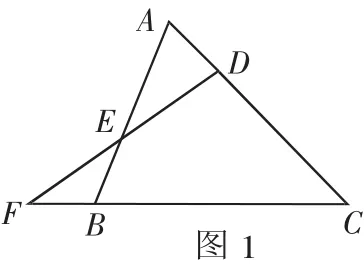
例 题 如图1，△ABC中，∠CAB=∠CBA，D是AC上一点，F是CB的延长线上一点，且AD=BF，DF交AB于E.求证：EF=ED.

分析：本题是证明线段相等的题目，此题不可能通过直接证两个三角形全等来得出结论，因此必须通过添加辅助线，添加方法不同，便得到不同的解题思路（如三角形全等、中位线定理、相似三角形等）.

证法一：过D作DG∥CF交AB于点G，则有：

∠DGA=∠CBA.

因为∠CAB=∠CBA，

所以∠DGA=∠CAB=∠DAG.

所以AD=DG.

因为AD=BF，

所以DG=BF.

又因为DG∥CF，

所以∠GDE=∠EFB.

又因为∠GED=∠FEB（对顶角相等），

所以△DGE≌△FBE.

所以EF=ED.

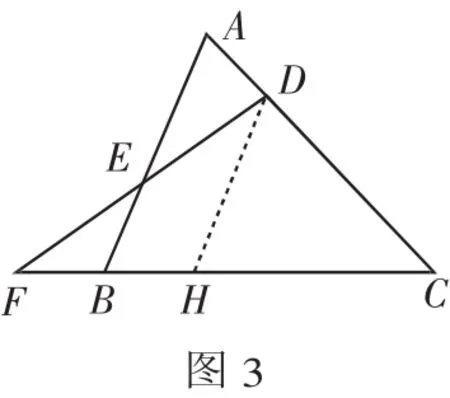
证法二：过D作DH∥AB交BC于H，则有：

∠CHD=∠CBA，

∠CDH=∠CAB.

因为∠CAB=∠CBA，

所以CA=CB，∠CHD=∠CDH.

所以CH=CD.

所以BH=AD.

因为AD=BF，

所以BH=BF.

又因为EB∥DH，

所以BE是△DFH的中位线.

所以EF=ED.

证法三：过F点作FM∥AC交AB的延长线于M，则有：

∠FMB=∠CAB.

因为∠CBA=∠CAB，∠CBA=∠FBM

所以∠FMB=∠FBM.

所以FM=FB.

因为AD=BF，

所以FM=AD.

因为∠FME=∠CAB=∠DAE，

∠FEM=∠DEA，

所以△FME≌△DAE.

所以EF=ED.

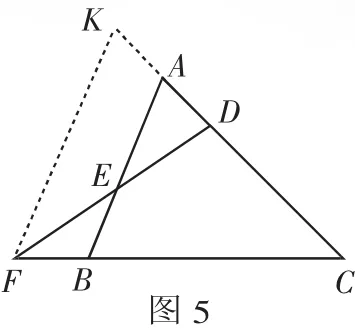
证法四：过F点作FK∥AB交CA的延长线于K.

因为FK∥AB，∠CBA=∠CAB，

所以AC=BC，CF=CK.

所以AK=FB.

因为AD=BF，

所以AK=AD.

又因为FK∥AB，

所以AE是△DFK的中位线.

所以EF=ED.

证法五：过C点作CN∥DF交AB的延长线于点N，则△FBE∽△CBN.

所以EF=ED.

证法六：过C点作CP∥AB交FD的延长线于P，

因为AB∥CP，

所以EF=ED.

当然，此题还有其他证法，有兴趣的读者可以继续探讨.在教学中，多对学生进行这样的训练，能引起学生的学习兴趣，提高学生的灵活分析、解决问题的能力，可以起到事半功倍的效果.