观解一类不等式组问题
2012-08-27高晓兵黄永秋
☉高晓兵 黄永秋
1.广西北部湾职业技术学校 2.广西浦北县第六中学
江就好老师在《初中数学教与学》2011年第6期上发表的文章《例谈用数形结合法解一类不等式组问题》,通过几个实例较详细地介绍了不等式组的数轴解法,具有较好的数学思想性和可操作性,但它须经历“作图、看图、表达”三个环节,三个环节紧密相联,不容失误,然而在细细品读之后,发现数轴法的求解过程比较复杂,尤其对于含参情形,学生并不能很好地掌握.在深入研究数轴法的观察及表达习惯,全面总结不等式组的基本特征后,笔者归纳出一种全新的方法——观解法,对于江老师文中所给例题,能做到轻松快捷且准确地求解,当然更复杂的情形,此法依然快捷自如.下面就简要介绍一些基本思想与具体的思路,同时通过几个例题向大家介绍此法.
一、观解法的简要介绍
观解法立足于数轴法,它完全按照向右观察和表达数轴的习惯,预先要求将不等号的开口方向全部统一向右,当然左边空时系负无穷大,而右边空则正无穷大.同时此法结合在数轴上不等式组的公共解集明显由两边向中间靠拢的特征,左边部分向中间靠拢时呈向右趋势,而在数轴上越往右越大,所以“左大”,同理右边部分向中间靠拢时呈向左趋势,而在数轴上越往左越小,所以“右小”,所以它的取值原则为“左大右小”.综上可以归纳出观解法求不等式组的基本思路为:⑴确定每一个不等式组的解集;⑵依向右观察和表达数轴的习惯,统一所有不等号开口方向向右,约定左边空负无穷大,右边空正无穷大;⑶依“左大右小”的原则确定不等式组的解集;⑷检查解集,若所得解集不成立,则此不等式组无解.
二、不含参数的不等式组
例1 解下列一元一次不等式组:


依“左大右小”得不等式组的解集为11<x<20.
问:为什么解集是 11<x<20,而不是 11≤x<20 或者其他结果呢?
答:因为11≤部分能取到最小值11,而11<部分任取一个数都大于11,所以左边较大的是11<;同样地,≤20部分能取到最大值20,而<20部分任取一个数都小于20,所以右边较小的是<20.
三、含有参数的不等式组
A.m≥3 B.m=3 C.m<3 D.m≤3

将不等式组解集中不等号开口变为向右有3<x.
现依“左大右小”的定值原则可得m≤3,故选D.
疑惑1:为什么是m≤3,而不是m<3、m>3或别的答案?
解惑 1:依“左大右小”,显然 m<3,因为如果 m>3的话,解集将是m<x,不合题意.
综上分析,可得m≤3.
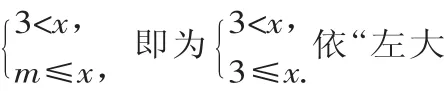

依题意不等式组有解集-1<x<1,现对照左右数值,可得

所以(a+1)(b-1)=(1+1)(-2-1)=-6.
A.6<m<7 B.6≤m<7 C.6≤m≤7 D.6<m≤7
而题意指出该不等式组有4个整数解,可以推知此4个整数解为 3、4、5、6.
为了3≤x<m只能取到3、4、5、6这四个整数解,则有6<m≤7,故选 D.
疑惑 2:为什么是6<m≤7,而不能是6≤m<7或其他情形呢?
解惑2:依题意,可以明显推断出6<m<7.接下来分析两个端点的情形.假设m=6,此时解集为3≤x<6,它只含三个整数解3、4、5,不合题意,故 m≠6;再假设 m=7,此时解集为 3≤x<7,它能取到四个整数解 3、4、5、6,符合题意.综上所述,可得 6<m≤7.
诚然,观解法立足于数轴法,却优于数轴法,它简化了求解的环节与过程,提高了速度与准确度,弱化了求解难度,同时它同样能直观快捷地求解出含多个不等式、端点不易确定等复杂情形以及含有参数的情形.只要熟练掌握和运用此法,不等式组问题将会变得非常简单.
1.高晓兵.“遥望”交并问题[J].考试周刊,2011(25):82.
2.江就好.例谈用数形结合法解一类不等式组问题[J].初中数学教与学,2011(06):20~21.
