灵活多变求几何图形阴影面积
2012-08-27湖北仙桃市三伏潭一中王丹仿
☉湖北仙桃市三伏潭一中 王丹仿
探求与圆有关的阴影面积一直是中考命题的一种题型,尤其是近几年来,考题新颖,还有一定的难度.不少同学对这类题型感到头疼.为了帮助同学们掌握这类题型的解题方法,特作如下归纳总结.
一、规则图形求差法
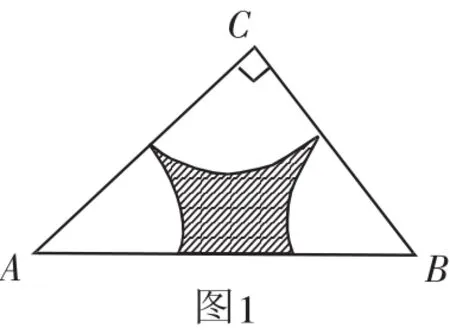
有些阴影部分是由一些规则图形拼接后留下的空当,这类问题可以先求出规则图形的面积,再求差即可解决.
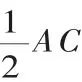

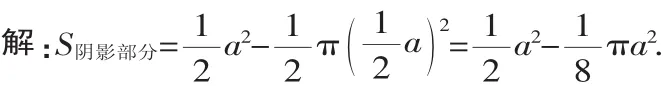
点评:仔细观察图形,搞清阴影部分的构成情况,是正确求解的基础.
例2 如图2,圆心角都是90°,半径分别为3和1的扇形AOB与扇形COD按图示方法叠放在一起,连接AC、BD,求图中阴影部分的面积.
分析:图中阴影部分看起来比较复杂,但仔细观察就会发现,由于△AOC≌△BOD,若将△BOD逆时针旋转90°至△AOC的位置后,阴影部分的面积实际上是两个半径分别为3和1的扇形面积之差.
解:因为OA=OB,∠AOC=∠BOD,OC=OD
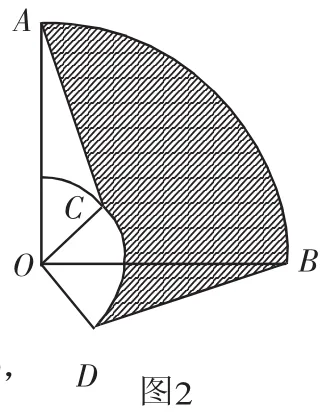
所以△AOC≌△BOD.
点评:图中阴影部分也可看做将扇形COD逆时针旋转∠AOC的度数后,扇形AOB与扇形COD面积之差.
二、转化图形求和法
有些阴影部分的面积,直接求比较困难,需要利用等积变换转化为其他图形的面积.
例3 如图3,半圆的直径AB=40,C、D是这个半圆的三等分点,求弦AC、AD和弧CD围成的阴影部分的面积.
分析:不难证明CD∥AB,图中阴影部分是弓形CD和△ADC面积之和,利用S△ADC=S△DOC, 即可将阴影部分转化为扇形COD.
解:因为C、D是半圆的三等分点,所以∠COD=∠AOC=∠BOD=60°.
因为OC=OD,
所以△COD是等边三角形.
所以∠DCO=∠CDO=60°.
所以CD∥AB.

点评:利用平行线间的距离处处相等可进行等积变换.
三、分割图形求差法
有些阴影部分整体求比较困难,可以先分割为几个部分,分别求面积后,再相加.
例4 如图4,同学们要在一块边长为a的正方形空地上种草,他们设计了如下图案,其中阴影部分为绿化面积,求绿化面积.
分析:图中阴影部分可通过连接BD将其分割成两块,先求出其一半,即可得整个阴影部分的面积.
解:连接BD.
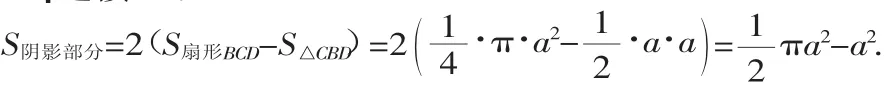

点评:(1)本题将阴影部分先分割为两个相同部分,再将其中的一部分分割为一个扇形和一个三角形面积之差.
(2)图中阴影部分的面积也可看成由扇形ABD加扇形BCD的面积再减去正方形ABCD的面积求得.
总之,求阴影部分的面积要在分清类别的情况下,采取相应的对策.当然,各种方法之间并无绝对界限,解决问题的途径不一定只有一个,只要同学们多思考多观察,一定会找到相应的对策,甚至能一题多解.
