例析勾股定理的应用

☉江苏南通市通州区兴仁中学 张玉娟

勾股定理揭示了直角三角形中三边之间的数量关系，几何中的很多计算问题都可转化到直角三角形中，用勾股定理来解决.围绕着勾股定理，出现了许多形式新颖，内容丰富的新型试题，这些新题，既考查了对勾股定理的理解、掌握和运用，又考查了同学们的创新能力.现采撷几道典型试题，进行分类说明，供大家参考.

一、利用勾股定理求面积

例1 如图1是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A、B、C、D的面积分别是3、5、2、3，则最大正方形E的面积是（ ）.

A.13 B.26 C.47 D.94

解析：因为勾股树中每相邻的三个正方形围成一个直角三角形，所以正方形A、B边长的平方和等于正方形F的边长的平方，即正方形A与正方形B的面积之和等于正方形F的面积，从而正方形F的面积为8；同理可得正方形G的面积为5；再利用上述结论，正方形E的面积等于正方形F和G的面积之和，故选择A.

评注：解决这类题的关键是抓住题目的特征，找出本题图形中的隐藏规律：如果把大正方形作为第一层，两个小正方形作为第二层，那么第二层的两个小正方形的面积之和等于第一层正方形的面积.

二、利用勾股定理求最短距离

例 2 如图2，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（ ）.

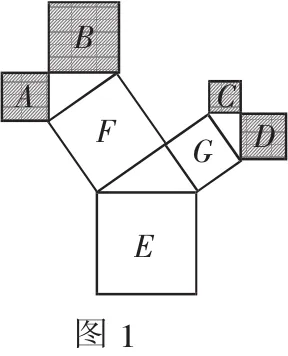
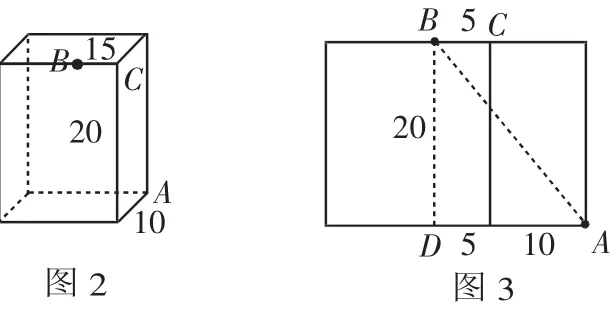
解析：因为蚂蚁从A到B点沿着长方体的表面爬行，因此将长方体侧面展开成平面图形，右图3是展开图的一部分，其中过B点作对边的垂线段，得到BD=20；由题意可知AD=15.根据“两点之间，线段最短”得A点到B点的最短距离为AB的长，在 Rt△ABD 中，∠ADB=90°，由勾股定理得：BD2+AD2=AB2，解得AB=25.即从A点到B点的最短距离为25，故选择B.

评注：求立体图形表面上两点间的最短距离，一般情况下，是将立体图形展开成平面图形，然后构造直角三角形，利用勾股定理去解答.

三、利用勾股定理求事件的概率

例3“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图4，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是（ ）.

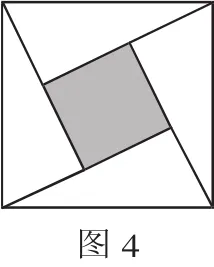
解析：这是典型的弦图，我们很容易得出中间阴影部分是一个正方形，而且边长为2；再根据勾股定理求出大正方形的边长为.因为所有正方形都有相似性，所以本图中小正方形与大正方形的面积比为对应边的比的平方，即1∶5；再根据概率公式求出投掷一次飞镖扎在中间小正方形区域（含边线）的概率是，故选择C.

评注：本题是集勾股定理、三角形、四边形、相似的性质、概率等为一体的综合题，考查比较全面.

四、利用勾股定理求圆的直径

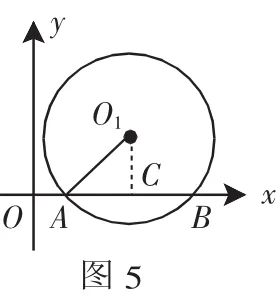
例4 如图5，已知⊙O1与坐标轴交于 A（1，0）、B（5，0）两点，点 O1的纵坐标为.求⊙O1的半径.

解析：过点O1作O1C⊥AB，垂足为C，则有AC=BC.

由 A（1，0）、B（5，0），得 AB=4，则 AC=2.

在Rt△AO1C中，O1的纵坐标为

所以⊙O1的半径

评注：本题考查求平面直角坐标系中点的坐标，以及垂径定理的应用，要求利用勾股定理去求圆的直径.

五、用勾股定理测河宽

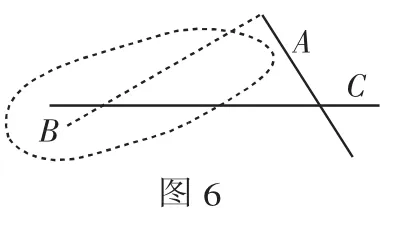
例5 如图6，阴影表示长江宜昌段某处的江面部分，为了测量A、B两点之间的距离，观察者确定三个测点 A、B 和 C，分别测∠BAC=90°，又量得BC=1300m，AC=500m，于是，他们可计算A、B之间的距离.

解析：本题是应用勾股定理解决实际问题.

由测量可知：∠BAC=90°，直角边AC=500m，斜边BC=1300m.根据 AB2=BC2-AC2，得：

所以AB=1200m.

评注：本题是勾股定理的实际应用，考查实际生活中不能够直接测量的地方.构造直角三角形，利用勾股定理求出两点之间的距离.

六、用勾股定理量物高

例6 有这样一段古诗和图片：“如图7，今有竹高一丈，末折抵地，去本三尺.问折者高几何.”请你回答这首诗里提出的问题.写出解答这首诗的方法和步骤.

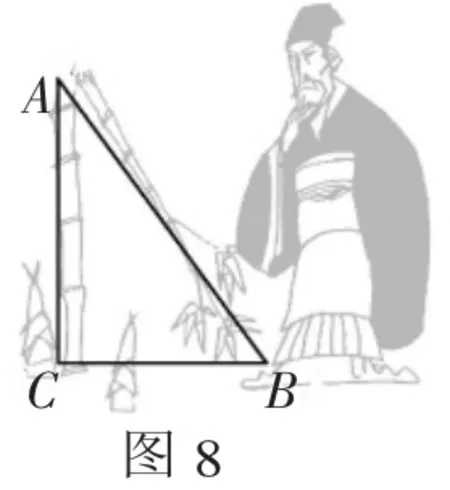
解析：根据诗里所描述的情景，把它转化为数学问题，画出图8.

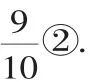
则原处还有4.55尺高的竹子.

评注：本题是古代有趣的勾股定理应用题，同时也是一道实际生活应用题，考查了同学们建模的思想方法.

七、用勾股定理求周长

例7 有一块直角三角形的绿地，量得两直角边长分别为6m、8m，现在要将绿地扩充成等腰三角形，且扩充部分是以8m为直角边的直角三角形，求扩充后等腰三角形绿地的周长.

解析：在 Rt△ABC 中，∠ACB=90°，AC=8，BC=6，由勾股定理知AB=10.扩充部分为Rt△ACD，扩充成等腰△ABD，应分为以下三种情况：

①如图9，当AB=AD=10时，可求得CD=CB=6，则△ABD的周长为32m.

②如图10，当AB=BD=10时，可求得CD=4，由勾股定理得：

评注：本题既考查勾股定理的应用，又考查等腰三角形的性质，同时比较全面地考查同学们分类讨论思想的掌握情况.

总之，勾股定理已有数千年的历史，在古代、当今和未来都有广泛的应用.勾股定理在实际中应用非常广泛，与实际生活联系密切.在解决实际问题时，关键是把实际问题的量转化为直角三角形的三边，从而使用勾股定理来解决.