全概率公式解题方法探究

聂红科，范慧歆

(郑州职业技术学院，河南 郑州 450052)

全概率公式是概率论中一个重要的公式，也是学习中的一个难点。针对全概率公式，剖析其内涵并将其推广，后引入图表法，数形结合地梳理各层次关系，使抽象的问题直观化、简单化、明了化，能有效解决较复杂问题。

1 公式法

1.1 直接运用全概率公式

定义1［1］设 S为试验 E的样本空间，B1，B2，…，Bn为E的一组事件。若

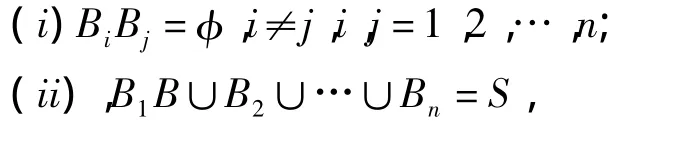
则称B1，B2，…，Bn为样本空间S的一个划分。

定理1［1］设试验E的样本空间为S，A为E的事件，B1，B2，…，Bn为 S 的一个划分，且 P(Bi)＞0(i=1，2，…，n)，则

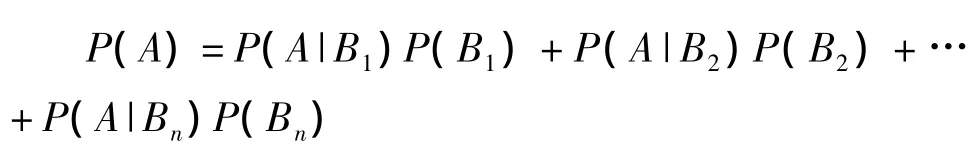
上式称为全概率公式。

注1 全概率公式是在加法公式和乘法定理的基础上推导出来的，从定理1的表达中我们可以看出，P(A)实质就是各条件概率P(A|Bi)的加权平均值，而各个条件事件Bi发生的概率P(Bi)就是权重。

注2 在具体运用定理1的时候，如何选择样本空间S的划分B1，B2，…，Bn显得尤其重要。在选择划分的时候，一定要把产生结果的原因全找出来，不能遗漏，并且保证B1，B2，…，Bn为两两互不相容事件。选择恰当的划分将会使计算大为简化，如果选择不当，将会影响计算，甚至导致错误。这也是公式在运用时的难点。

例1 设有来自一个地区的考生的报名表分别是10份，15份和25份，其中女生的报名表分别是3份，7份和5份，随机地取一个地区的报名表，从中抽出一份，求抽到的是女生表的概率。

分析 引起抽到女生表的所有原因是来自三个不同的考区都包含有女生，这构成了样本空间的一个划分。显然，由条件，各考区女生表的概率可求，可直接用全概率公式求解。

解:以事件A表示“抽出报名表是女生表”，事件Bi表示“报名表是第 i个考区的”(i=1，2，3)，则有

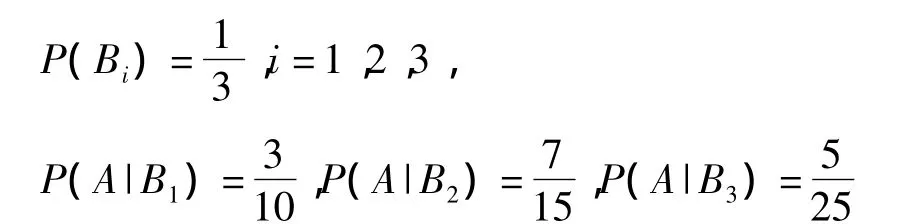
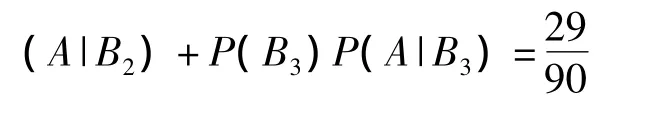
1.2 全概率公式的推广

定理1的条件要求B1，B2，…，Bn为两两互不相容事件，但有时候，我们遇到的题目所得到的事件列并不满足定理1的条件，下面给出一个更一般的结论。

推论1 设S为试验E的样本空间，{Bn}为试验E中任意事件列，并且对一切n有P(Bn)＞0，∪n

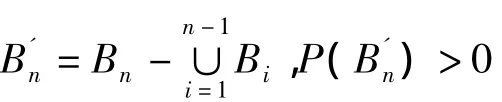
证明:不妨设 j＜ k，j，k=1，2，…，从而有 j≤k －1

例2 我军甲、乙、丙三艘炮艇向同一敌舰射击。设甲、乙、丙射中的概率分别为 0.3，0.5，0.8。又设甲击中时敌舰沉没的概率为0.7，甲击不中乙击中时敌舰沉没的概率为0.4，只有丙击中时敌般沉没的概率为0.1，求敌舰沉没的概率。

分析 对于目标事件“敌舰沉没”，虽然是由于“甲击中”，“乙击中”，“丙击中”所引起的，但是这三个事件并不一定是不相容的。故不能直接用定理1，需要用推论1求解。

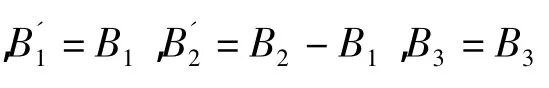
由题目可知:

在用公式法解题时，往往会一不小心就出错了，为了提高解题效率，下面给出图表法。

2 图表法

用公式法解题时，往往由于事件比较多，常常会有遗漏或在计算时分不清主次，弄不清楚哪些是条件事件以至于产生错误。下面我们给出解此类题目的图表法，也称为概率树法。它思路清晰，不容易出错，是数形结合的好方法，能很好地解决上面的问题。

图表法就是按事件发生的先后顺序作出图，它的形状像一棵树，有根、分支、节点和末梢，然后再按原途返回求解。见下图所示:

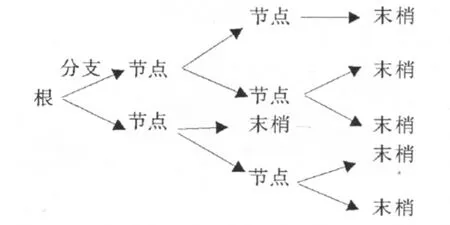
图表法主要是利用乘法原理，在上面树形结构中，在一整个分支上，从根到末梢，各事件发生的概率等于各段分支上概率的乘积。下面，我们就用图表法给出例1和例2的解法。

例1 解法二:以事件A表示“抽出报名表是女生表”，事件Bi表示“报名表是第i个考区的”(i=1，2，3)，作出图表

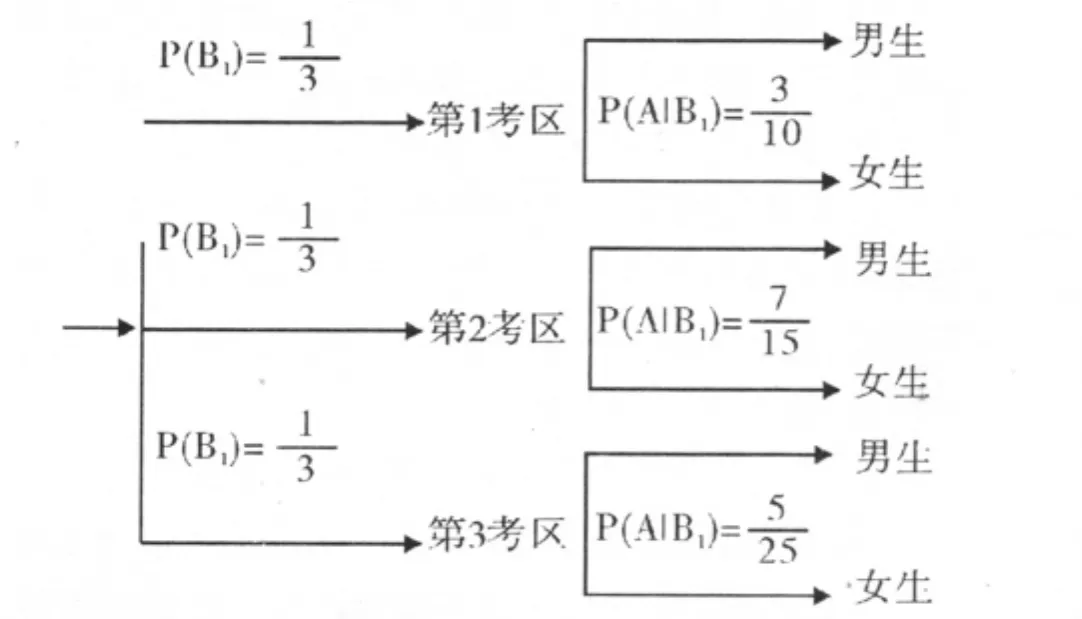
从上图看出，最终抽到女生表的路径有三条，把每条路径的概率相乘再相加可得

例2 解法二:设表示事件“敌舰沉没”

依题意作出树形图表

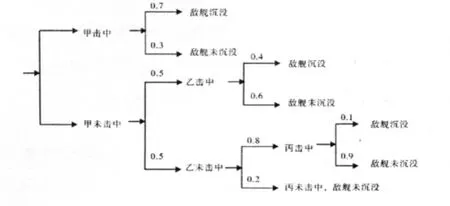
将图中每条敌舰沉没路径的概率相乘再相加可得

注3 从上面的例子中我们可以体会到，图表法思路更加清晰，解题更加方便，不容易出错，在具体应用时可灵活运用。当层次分的越多越复杂时，图表法更能显示出它的优越之处，但是，在使用时必须要注意:每一分支后的几个事件必须是互不相容事件;从第一个节点之后，路径中的概率均为条件概率。

［1］盛骤，谢式千，潘承毅.概率论与数量统计［M］.北京:高等教育出版社，2001，(12).

［2］魏宗舒.概率论与数理统计教程［M］.北京:高等教育出版社，2005.