小样本条件下一种旋转机械振动状态阈值的确定方法及应用

2012-08-18李会鹏明廷锋

武汉理工大学学报（交通科学与工程版） 2012年5期

李会鹏明廷锋贺国

（海军工程大学船舶与动力学院武汉 430033）

振动是影响大型旋转机械安全运行的重要因素，因此对旋转机械的振动监测可及时发现问题，有效保障设备的安全运行.自助法和随机加权法都是利用样本重采样技术进行样本扩充的方法［1－3］.经仿真计算和实际应用表明，随机加权法较自助法有更高的精确度［4］.然而，这两种方法对样本信息依赖较大，若直接运用该方法对样本进行扩充，可能会产生较大的误差.本文综合运用随机加权法、Bayes方法和信息融合方法，对小样本条件下振动阈值的设定方法进行研究，以期最好地解决小样本条件下的阈值设定问题.

1 特征值的均值与方差估计方法

1.1 随机加权法

设未知参数α服从正态分布，大小相互独立.记α＝（x1，x2，…，xn）为现场子样，μ和σ2分别为α的均值和方差，运用随机加权法估计μ和σ2，具体步骤如下.

1）计算现场子样的均值¯x和方差s2，即有：

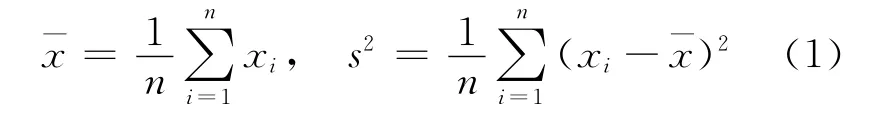
2）产生N 组Diricklet随机向量，V（i）＝（Vi1，Vi2，…，Vin），i＝1，2，…，N，这里（Vi1，Vi2，…，Vin）为参数（1，1，…，1）的 Diricklet随机向量，记它的联合分布为（1，1，…，1）.它可按如下方法产生：

设v1，v2，…，vn－1是（0，1）上均匀分布的随机变量v的独立同分布子样，对其按从小到大的次序重新排序，记为v1≤v2≤…≤vn－1.又记v0＝0，vn＝n，Vij＝vj－vj－1，j＝1，2，…，n.那么，（Vi1，Vi2，…，Vin）的联合分布就是（1，1，…，1）.它就是所需的Diricklet随机向量.

分布参数μ，σ2的均值估计分别为

1.2 验前分布的信息融合

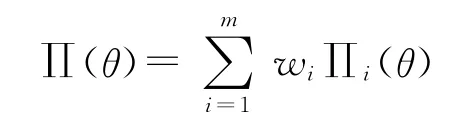
式中：wi为第i个信息源的权重因子＝1.

样本方差

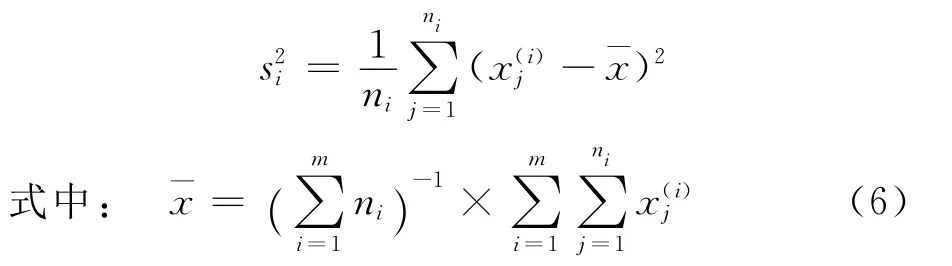
1.3 Bayes统计推断方法

在正态分布条件下，未知参数β的均值μ与方差σ2的联合共轭分布是正态－逆Gamma分布，即（μ，σ2）～N－IGa.式中：μπ，kπ，为共轭先验分布∏（θ）的超参数.根据文献［8－9］可以得出以下结论.

1）（μ，σ2）的后验分布也是正态－逆 Gamma分布 N－IGa.

2）μ的后验分布是自由度为vk的学生氏分布），即μ／

3）σ2的后验分布是逆Gamma分布

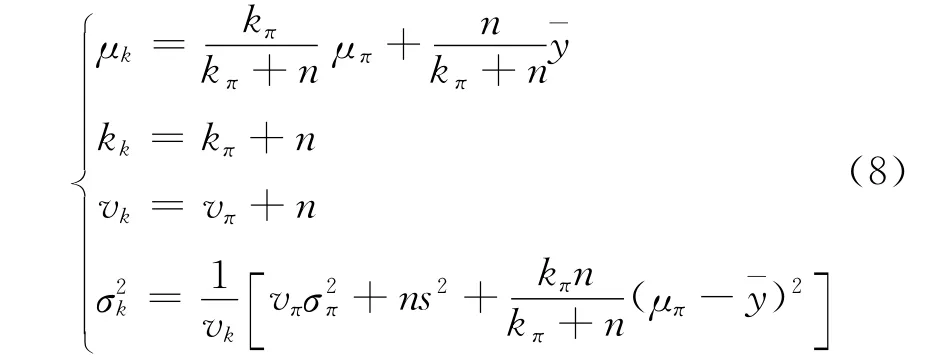
2 小样本条件下特征值的统计参数估计方法

结合上述分析和旋转机械振动的特征值－振动有效值分布规律，根据数理统计分析的基本理论和一般步骤，综合运用Bayes方法、信息融合方法和随机加权法，得到振动有效值分布特性统计参数估计流程，见图1.

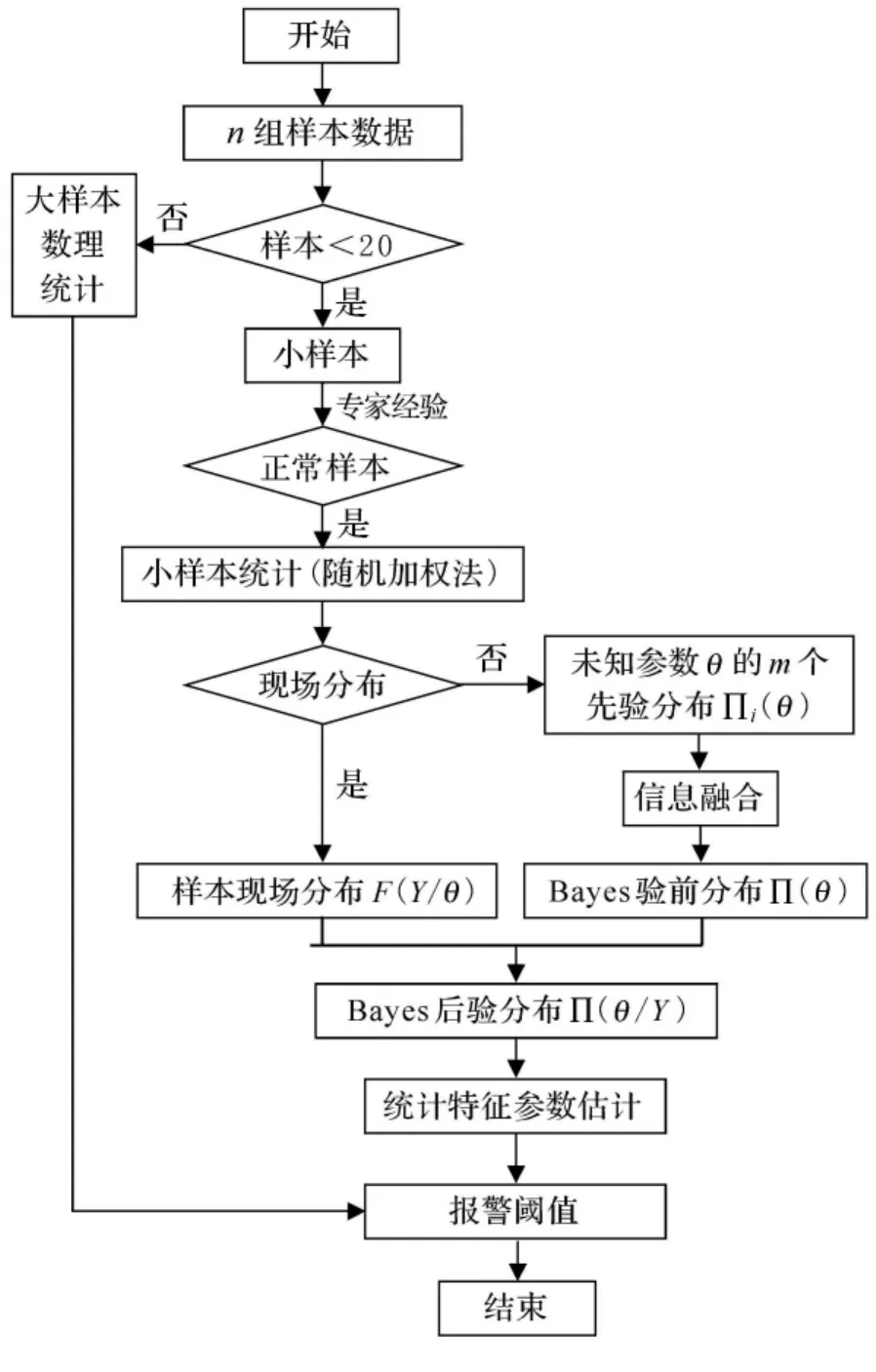
图1 小样本下旋转机械振动特征值的统计参数估计流程

该流程的主要思路是：首先对n组样本的数据量进行判断，若样本数小于20，运用小样本统计方法.其次，利用专家经验对各个小样本进行判断，选择正常的样本进行小样本统计运算；再次，判断正常样本是属于现场样本还是属于历史样本：若样本属于现场样本，则通过随机加权法可以得到现场样本的分布；若样本属于历史样本，则利用随机加权法可以得到先验分布.在得到各个历史样本的先验分布的基础上，运用信息融合方法对各个样本信息进行信息融合得出样本信息的验前分布；最后运用Bayes统计推断方法进行后验推断，获得所需参数的特征值估计，再依据3σ方法设定合适的阈值.

3 仿真研究

3.1 随机加权法估计样本的均值与方差

根据1.1中随机加权法对其均值和方差的分布情况进行估计：样本M 均值μM～N（14.33，0.462），方差σ2M～N（2.13，1.342）；样本 N 均值μN～N（14.79，0.612），方差～N（3.76，1.732）；样本Q均值μQ～N（15.36，0.682），方差～N（4.44，1.362）.

3.2 历史样本的信息融合

根据1.2中先验信息融合方法计算得到：w1＝0.599 0，w2＝0.401 0.

那么，样本信息融合后均值

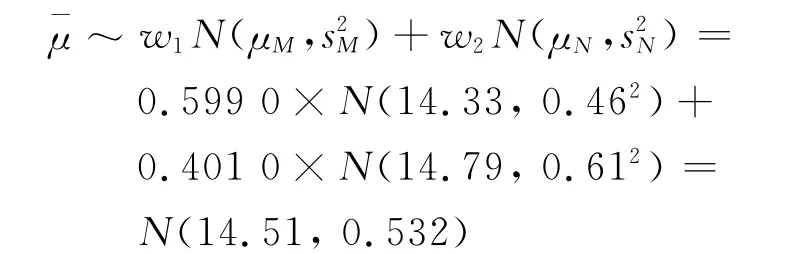
同理，得方差¯σ2～N（2.78，1.512）.

3.3 特征值统计参数的Bayes推断方法

令μ的先验分布表示为∏（μ），σ2的先验分布表示为∏（σ2）.由3.2的计算，得∏（μ）先验均值为＝14.51，先验方差为＝0.532；∏（σ2）的先验均值为＝2.78，先验方差为＝1.512.

根据1.3中的结论2和结论3的建立以下2组方程组

将上面两方程组联立，求得先验分布的超参数为

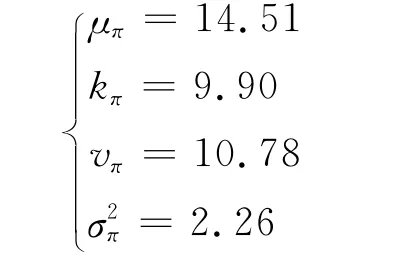
由1.3中的结论4，求得后验分布超参数为

因此μ的后验期望估计为

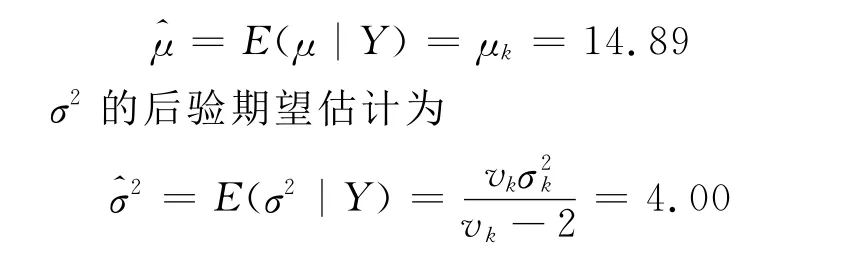
运用随机加权法、信息融合方法和Bayes统计推断获得参数的分布估计为N（14.89，4.00）.定义该方法为Bayes－随机加权法.将该方法与经典统计、随机加权法进行对比，见表1.

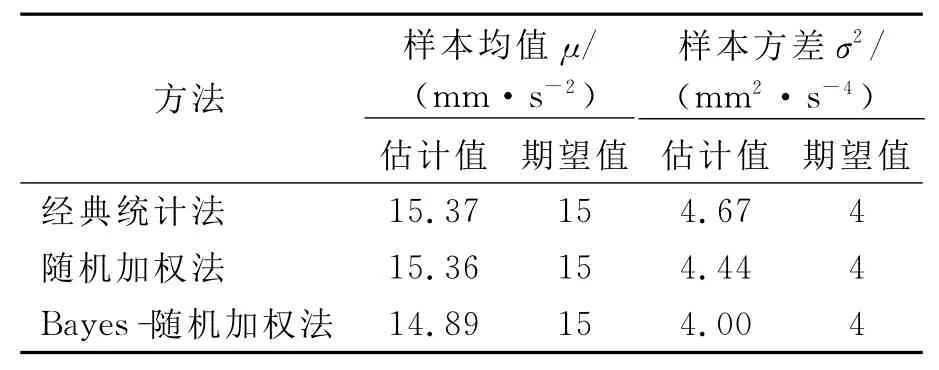
表1 统计参数估计结果对比

分析表1，随机加权法与经典统计法相比，它的方差估计值更小，其均值估计值变化不大.而Bayes后验推断融合了先验分布和现场信息进行后验估计，使得计算出后验估计的均值和方差更加逼近期望，它对均值估计值与期望值非常接近，它对方差的估计值与期望值一致，取得了较理想的结果.由此可见，本文给出的Bayes－随机加权法对小样本统计特征推断有一定的优越性.

4 实例应用

对一台离心泵机组故障模拟平台的振动状态进行监测.现有历史样本A，B和C，分别为：样本A（31.50，32.95，28.50，30.84，30.16，32.71），样本B（22.82，22.96，23.67，21.92，21.67，22.69），样本C（23.97，23.65，23.77，25.03，22.93，24.54）.并有现场样本D（23.46，25.59，25.96，24.86，24.08，25.23），上述样本振动数据均为该离心泵机组水平方向加速度振动有效值，单位为mm／s2.

4.1 样本信息的均值与方差估计

根据1.1中随机加权法计算得到样本A均值μA～N（31.10，0.572），方差～N（2.78，0.852）；样本B 均值μB～N（22.62，0.252），方差～N（0.53，0.162）；样本 C 均值 μC～N （23.98，0.252），方差～N（0.53，0.172）；样本D 的均值μD～N（24.86，0.332），方差～N（0.89，0.252）.

4.2 先验信息的分析与融合

依据专家经验知悉该离心泵机组故障具有“浴盆曲线”特性，见图2，起始段故障率较高，为磨合期，经过一段时间后，故障率减小，为偶发期，随着运行时间的增加故障率开始增加，即为耗损期.

图2 离心泵机组故障概率模型图

依据图2所示设备故障概率模型图，对先验样本A，B和C进行分析，可知样本A的振动数据偏大.结合该监测样本的获取时机恰好是在设备刚投入使用不久.根据图2知，该设备正处于磨合期，因此振动较大，波动也较为明显；而样本B和C的振动较为平稳，波动较小.因此，在选择先验样本时，为避免振动阈值设定不合理，应把样本A舍去，仅选用样本B和C作为先验信息.

根据1.2中先验信息融合方法.计算wi得到：w1＝0.502 4，w2＝0.497 6.

那么，样本信息融合后均值

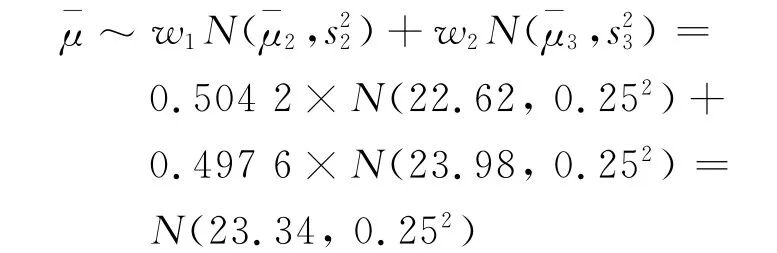
同理可得样本信息融合后方差¯σ2～N（0.53，0.162）.

4.3 Bayes统计推断方法估计统计参数

计算过程与3.3一致，得μ的后验期望估计为

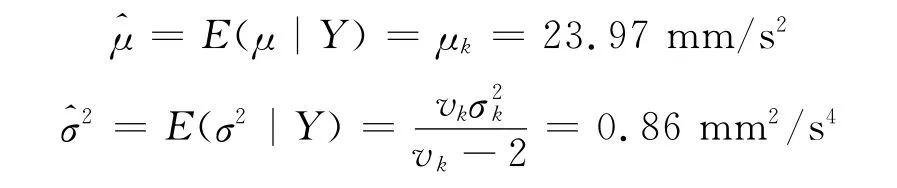
4.4 振动有效值的阈值设定

通常，设备振动较小时不认为是故障状态，所以只需设定报警上限，而不用设定报警下限.根据阈值评定准则，可求出阈值的报警限：

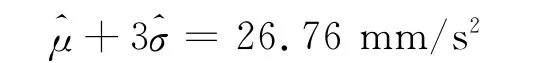
同理，随机加权法设定的报警阈值为27.53，利用经典统计法设定的报警阈值为27.68，单位均为mm／s2.

现模拟离心泵机组的地脚螺栓松动故障，测取并计算得到10组故障样本（水平向加速度振动有效值）：G（30.17，27.61，28.72，27.16，28.68，29.46，28.08，29.43，26.93，31.64），单位为mm／s2.分别利用Bayes－随机加权法、随机加权法和经典统计法设定报警阈值，结果见图3.

图3 离心泵机组水平向振动有效值报警线图

从图3可以看出：应用Bayes－随机加权法设定的报警线没有出现误报和漏报的情况，应用随机加权法设定的报警线出现2次漏报，应用经典统计方法设定的报警线出现3次漏报.由此可见，本文给出的振动状态阈值设定方法因为融合了验前信息，所制定的报警线更加的科学，得到最好的效果，而应用随机加权法制定的报警效果稍差，应用经典统计制定的报警效果最差.