对高考试题“多余条件”的分析

温见明

（赣县中学 江西赣州 341100

近几年全国各地物理高考，偶尔会出现试题“条件多余”的情况，命题者这样命题的目的是什么？是为了降低高考试题的难度，还是为了让试题的物理情景更加清晰？或者是两者皆有？现通过近几年的高考试题加以分析.

1 试题的“条件多余”结果唯一

【例1】（2008年高考全国卷Ⅰ第24题）图1中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点O由一不可伸长的轻绳相连，轻绳长为l.开始时，轻绳处于水平拉直状态，小球和滑块均静止.现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有粘性物质的固定挡板粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角θ＝60°时小球达到最高点.求

（1）从滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量；

（2）小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小.

图1

这里主要讨论第一问.

解法一：对系统，设小球在最低点时速度大小为v1，此时滑块的速度大小为v2，滑块与挡板接触前，由系统机械能守恒定律可得

对小球由最低点运动到左侧最高的过程中由机械能守恒定律可得

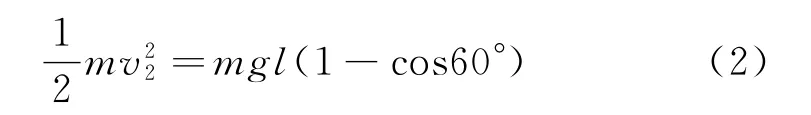
对滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量为（以向右为方向）

联立（1）～（3）式解得I＝－mv1，方向向左.

解法二：系统水平方向不受外力作用，对滑块和小球组成的系统，由水平方向动量守恒定律可得

由（1）和（4）式可得

接下来的解法同解法一.

由上述两种解法可知，没有“当轻绳与竖直方向的夹角θ＝60°时小球达到最高点”这个条件，也可正确解答出本题，命题者只是加入这一条件使试题情景更明了而已，也使得考生可从多个角度去思考，从而降低了本题的难度.

2 试题的“条件多余”结果可多种形式

【例2】（2009年高考福建卷第21题）如图2（a）所示，在水平地面上固定一倾角为θ的光滑绝缘斜面，斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为κ的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态.一质量为m、带电荷量为q（q＞0）的滑块从距离弹簧上端为s0处静止释放，滑块在运动过程中电荷量保持不变，设滑块与弹簧接触过程没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g.

（1）求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1；

（2）若滑块在沿斜面向下运动的整个过程中最大速度大小为vm，求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W；

（3）从滑块静止释放瞬间开始计时，请在图2（b）中画出滑块在沿斜面向下运动的整个过程中速度与时间关系v-t图像.图中横坐标轴上的t1，t2及t3分别表示滑块第一次与弹簧上端接触、第一次速度达到最大值及第一次速度减为零的时刻，纵坐标轴上的v1为滑块在t1时刻的速度大小，vm是题中所指的物理量.

图2

本题主要解答第（2）问.

解法一：滑块速度最大时受力平衡，设此时弹簧压缩量为x0，则有

从静止释放到速度达到最大的过程中，由动能定理得

联立（5）、（6）式可得

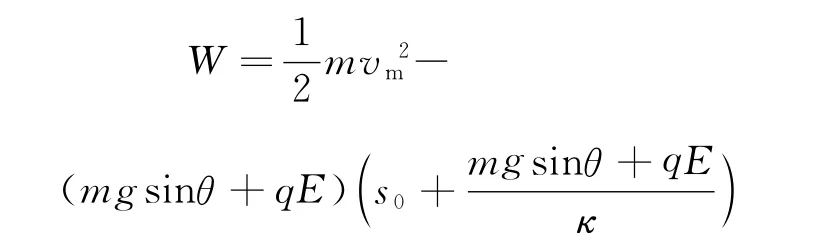
解法二：由于弹簧的弹力与形变量成正比，故弹力做的功可用求平均功的方法求解，即此过程弹簧弹力做的功为

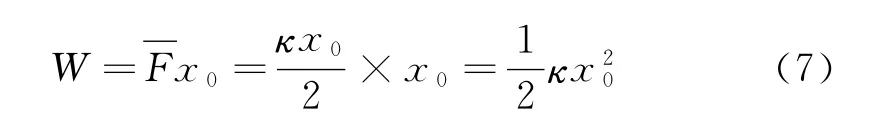
联立（5）、（7）式可得

显然，这两个答案的表达是不一样的，但从能量转化的角度来看却是等价的.这里第二种解法没有用到已知条件“若滑块在沿斜面向下运动的整个过程中最大速度大小为vm”，但这种求弹力做功的方法，高考考试大纲不作要求，故对大多数考生来说应该提供这个条件，但对程度较好的考生特别是参加了奥赛的考生来说，就会觉得此条件是多余的.

由上述二例不难看出，命题者应该是有意这样做，一方面可降低试题难度从而使试题更具有梯度，另一方面可使物理情景更清晰.