EMD 算法在检测电力故障信号中的应用*
2012-08-09曹德健
杨 彦 ,王 浩 ,曹德健,赵 力*
(1.盐城纺织职业技术学院,江苏 盐城 650500;2.东南大学信息科学与工程学院,南京 210096)
由于电力系统的复杂性,在远程传输以及运载中会产生的不平稳的故障信号,这也就使得信号突变的检测在电力系统中占有重要的地位。其常用的传统数学工具为短时傅里叶变换,短时傅里叶变换将信号划分为许多小的时间间隔,用傅里叶变化分析每个时间间隔,一边确定该时间间隔的频率。然而对于短时傅里叶变换,时间—频率窗口的宽度对于所有频率的谱具有不变特性,这一点不适合于非平稳信号的高频与低频部分的特性分析。后来很多工程应用者尝试将小波变换理论引入电力系统故障分析中,因为小波变换能够在时域和频域同时得到比较高的分辨率,然而对信号进行小波变换必须预先确定小波的基函数,且信号分解的效果取决于小波基函数的选择,并不能够保证最优的小波分解效果[1]。1998年,美国国家宇航局(NASA)的Norden和E.Huang 等人在对瞬时频率的概念进行深入研究的基础上,创立了希尔伯特-黄变换,该方法被认为是近年来对已傅里叶变换为基础的线性和稳态谱分析的一个重大突破[1]。它是一种基于经验模式分解EMD(Empirical Mode Decomposition)的时频分析处理方法。它将非平稳信号按不同尺度的波动或趋势逐级分解成若干个本征模式分量IMF(Intrinsic Mode Function),然后对IMF 进行Hilbert 变换,得到信号的时频谱图具有良好的时频分辨率,从而具有良好的局部视频特性表现能力,因此能够更加准确地反映原信号的特性,可以用来检测突变信号。该方法吸取了小波变换的多分辨率的优势,同时克服了小波变换中选取小波基的困难。能够更加准确地检测出突变信号,从而正确定位出信号的故障点。
1 电力系统中的故障信号
电力系统的不断发展,使得输送电压和容量的逐步提高,有输电线故障造成的损失也越来越大。电力系统主要有短路故障、断路故障、复杂故障。用Simulink 中的Power system 仿真工具包来进行故障信号仿真,通过仿真可以得到如图1 几种故障的A相电压信号波形图。
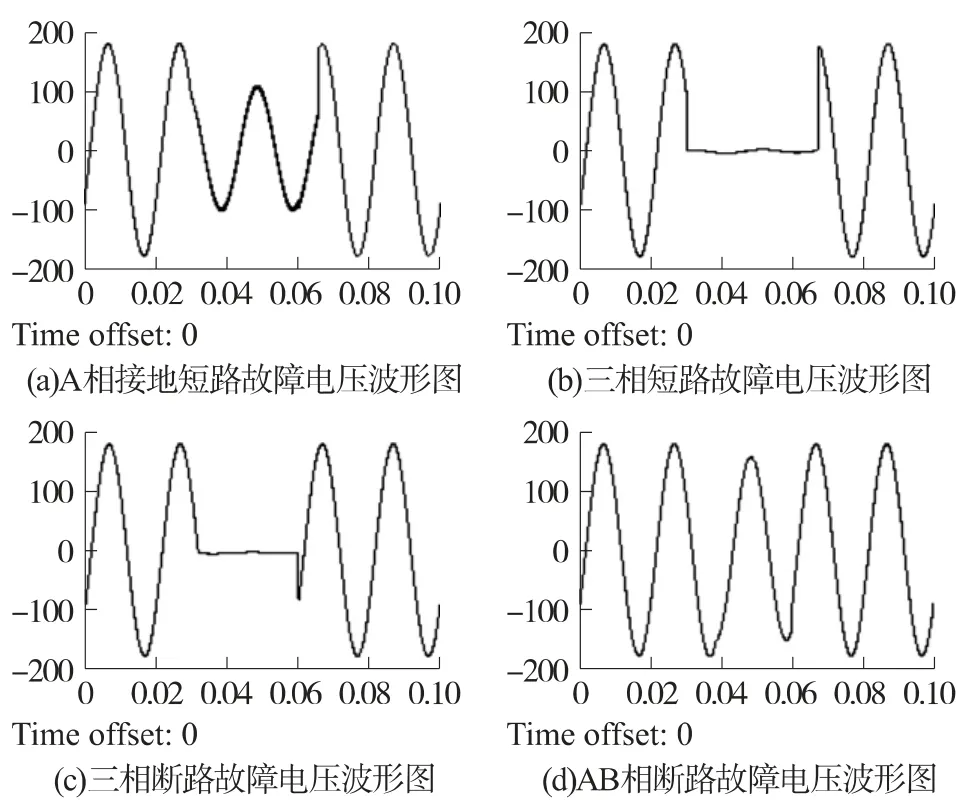
图1 几种故障的电压波形图
2 EMD 用于故障信号处理的基本原理
经验模式分解是1998年Huang 提出来的一种全新的信号处理方法[2-3]。它通过对信号的筛选将信号分解成不同频率的IMF,IMF 具有以下特点:第1 IMF 的极值(包含极大值和极小值)数与过零点的数目相等或最多相差一个;第2 在任意时刻,IMF 的上包络线与下包络线的均值必须是零。具体的分解过程如下[4]:
第1 步:首先找到待分析信号x(t)所有的极大值点并将其使用3 次样条函数插值(在下面做了描述)成为原数据序列的上包络线;找到x(t)所有的极小值点将其使用3 次样条函数插值成为原数据序列的下包络线,然后求出上包络线和下包络线的平均包络线m1(t);
第2 步:将原数据序列减去平均包络后即可得到一个去掉低频的新数据序列h1(t)=x(t)-m1(t);然后判断h1(t)是否满足IMF 的条件,若不满足,将h1(t)看作新的x(t),重复上述处理过程,直到h1(t)满足IMF 条件时,记c1(t)=h1(t),视为IMF1;
第3 步:将r(t)=x(t)-h1(t)看作新的x(t),重复以上(1)和(2)的步骤,即可以依次得到IMF2,IMF3,…,直到cn(t)或r(t)满足给定的终止条件时筛选结束。
按照上面的分解步骤,原始数据序列x(t)可以由这些IMF 分量及一个均值或者趋势项r(t)来表示:

其中每一个IMF 分量都代表一个特征尺度的数据序列,所以可以说EMD 过程实际上是将原数据序列分解成为不同特征波动的序列。

其中Re 表示取实部,ai(t)表示每一个本征模函数经希尔伯特变换后的瞬时振幅,fi(t)表示每一个本征模函数经希尔伯特变换后的瞬时频率。若以时间、瞬时频率为自变量,幅度以等高线的形式表示,则可以将三者之间的关系表示为一个三维时频谱,又称为Hilbert 幅度谱,简称为Hilbert 谱,记为H(f,t),则有

下面进一步来分析Hilbert 谱,定义边缘谱为h(f),有

其中T 表示信号序列的时间长度。根据边缘谱的表达式,可以看出,边缘谱是对三维时频谱在时间上进行积分,便形成了只有频率和幅值的二维的关系图,边缘谱表征了整组数据在每个频率点的积累的幅度值分布,而傅里叶频谱在每一点的幅度值表征了信号里有一个含有此频率的三角函数的组分,傅里叶频谱和边缘谱是不同意义的两种频谱与幅值关系表达式。
从上述理论,我们可以看出,EMD 算法是具有自适应性的,主要表现在:生成的基函数具有自适应性,IMF 的频率分辨率也是具有自适应性的,且同时具有滤波特性[5]。所以可以把EMD 分解看做是一组具有自适应特性的带通滤波器,其截至频率和带宽随被分解信号的不同而不同[6-7]。同小波变换相比,EMD 是有自适应的,而小波分析则没有,因为小波的分解尺度被选定,分解得到的时域波形就是固定频率段的,且频率段只与分析频率有关,与信号本身无关[8]。这就是EMD 相比于小波变换的优点。
3 EMD 方法存在的缺点与改进
EMD 分解的一个重要步骤是构造信号的上下包络线,从而得到信号的瞬时平均包络。Huang 等提出的以信号的极大值点来拟合上包络线,极小值点来拟合下包络线,其中拟合算法采用的是3 次样条插值方法。然而,我们知道,在信号的开始端和结束端往往不是极大值或者极小值点,因此3 次样条曲线容易在数据的两个端点出现发散现象,且EMD的过程也使得这种发散现象不只局限于端点处的小范围,而是伴随着每次的筛选过程逐渐往内传播,会引起最终结果较大的失真,这种现象称为“端点效应”。此外,我们知道,EMD 的过程就是对信号进行筛选的过程,筛选对信号有两个结果:第1,驼峰减少,使得极大值为正数或零,极小值为负数或零;第2,光滑了非对称幅度。然而过度的筛选会使得信号在幅度上失去物理意义,且当前的电力设备很多都不能满足这种过度的筛选迭代,在这里将这种现象称为过度筛选现象。
在电力系统的复杂环境下,信号波形可能含有多个谐波和噪声,端点效应影响程度可能会加大,所以需要采取一定的方法来改善这种端点效应造成的误差。目前抑制这种效应主要采用两种方法:第1,寻找更加精确的求解上下包络的方法来替代已有的3 次样条插值方法,比如有约束3 次样条插值法,分段幂函数法,高次样条插值法;第2,在信号的两端选取合适的极大值和极小值点,使上下包络线能够完整的包络整个信号。在这里,我们采用第2种方法来减少端点效应所带来的误差,由于电力信号在一般情况下非故障点表现为一系列正弦信号之和,故电力信号在非故障处可以看作周期信号,本文将端点处的值作为极大值或极小值进行处理,当端点值为正数时,将其作为极大值,对其取反作为极小值;当端点值为负数时,将其作为极小值,对其取反作为极大值。采用这种方法信号的包络线得到了很大的改善,能够减少端点效应所带来的误差,能够满足大多数电力设备的要求。
对于过度筛选现象,本文降低了筛选的要求,即降低了IMF 的要求。我们知道,当一个信号完全满足IMF 的要求时,其上下包络线是关于时间轴完全对称的,包络线均值是处处为零的。一般情况,即使在误差范围内,也需要进行很多次的筛选,在这里,Huang等人使用esd标准来降低筛选条件。esd的表达式为
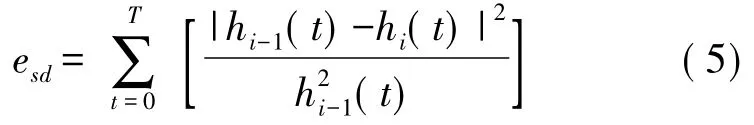
其中hi-1(t)和hi(t)分别代表经过第i-1 次和第i次筛选后的信号。一般情况下,当esd下降到0.2或者0.3 时,结束筛选过程。然而在esd中分母h2i-1(t)可能会出现零的情况,一般情况下这种为零现象是不可避免的,因此,esd的计算可能是不准确的。
从上面所述,当信号满足IMF 的要求时,其上下包络线是关于时间轴完全对称的,所以在筛选的过程中,信号的上下包络线是关于时间轴趋向对称的,那么我们可以根据包络线的对称程度来决定是否结束筛选。在这里,我们设第i 次的上下包络线数据序列分别为mup(n)和mdown(n),为了表示两个数据变量的近似程度,我们采用了相关系数标准。根据相关系数的定义,设ri为第i 次时的上下包络线相关系数,表达式为
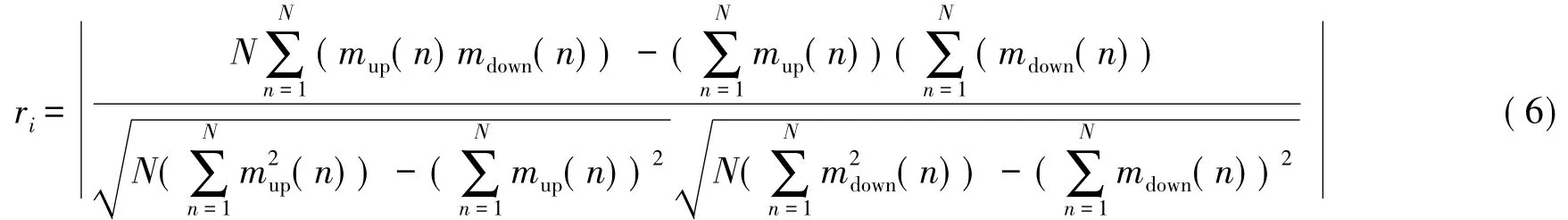
在一般情况下,我们将相关系数ri设置为大于等于0.985 时结束筛选。这样可以有效降低EMD算法的循环次数。
4 故障信号的EMD 仿真分析
图2为三相短路时的电压信号波形,我们在0.03 s 时设置故障,在0.065 s 时切除。
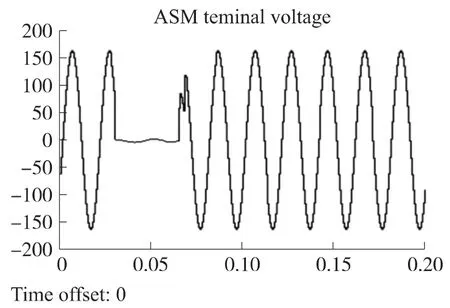
图2 三相短路时的电压信号波形
应用前两节方法对该信号进行EMD 分解,使用Matlab 仿真,结果为图3。
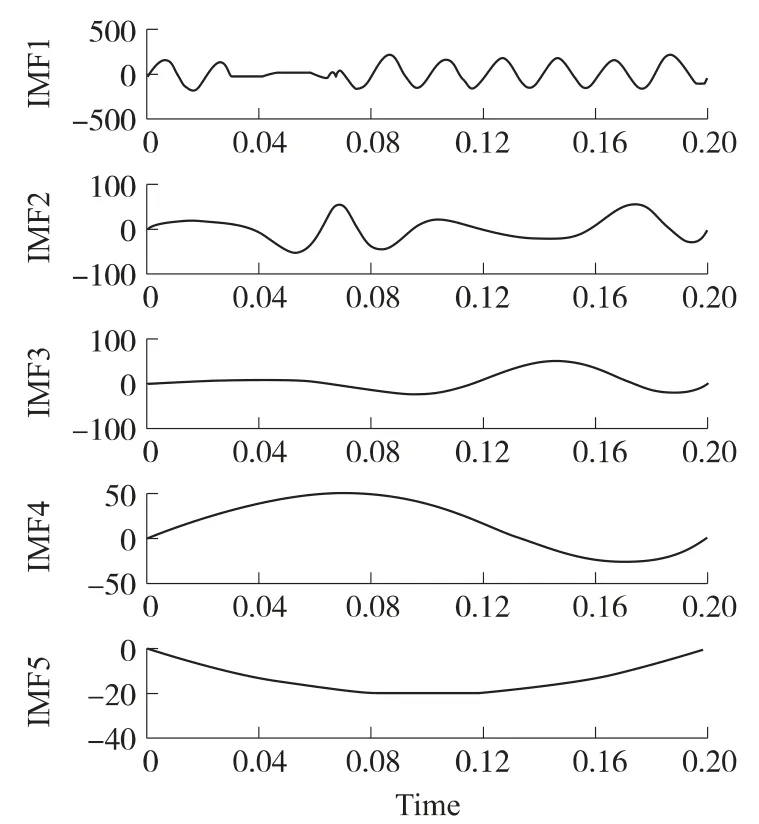
图3 信号的EMD 分解
对IMF 做希尔伯特变换,可得到图4。
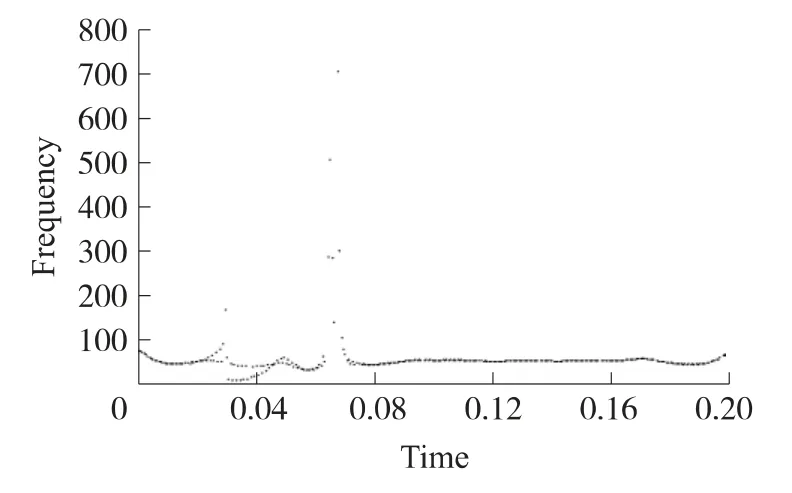
图4 希尔伯特变换后的时频关系图
通过在Matlab 中的放大观察,我们看到信号在0.030161和0.065125 出的频率很高,也就是故障发生和切除的时间,其误差0.125 ms~0.161 ms,故障时间定为准确,且运行时间在许可的时间内。
5 结论
电力系统对于继电保护装置的要求是快速,准确。本文采用了EMD 方法将信号分解,根据其IMF分量的希尔伯特变换得到信号的时频特性,从而能够准确定位故障发生的时间,在下一步的工作中,我们应该寻求对故障信号进行处理分类,使得继电保护器能够迅速的分辨出故障的类型,以便做出相应的动作。
[1]李天云,赵妍,李楠.基于EMD 的Hilbert 变换应用于暂态信号分析[J].电力系统自动化,2005,29(4):49-52.
[2]Huang N E,Shen Z,Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[C]//Proc.R.Soc.London A,1998,4:903-995.
[3]Huang N E,Stever R L.A New View of Nonlinear Water Waves:the Hilbert Spectrum[C]//Annual Review of Fluid Mechanics.1999,1:417-457.
[4]Balocchi R,Menicucci D,Varanini M.Empirical Mode Decomposition to a Approach the Problem of Detecting Sources from a Reduced Number of Mixtures[C]//Cancun,Mexico:Proceedings of the 25th Annual International Conference of the IEEE EMBS,2003.
[5]Raia V K,Mohanty A R.Bearing Fault Diagnosis Using FFT of Intrinsic Mode Functions in Hilbert-Huang Transform[J].Mechanical Systems and Signal Processing,2007,21(6):2607-2615.
[6]Wu Z H,Huang N E.Ensemble Empirical Mode Decomposition:A Nosie Assisted Data Analysis Method[R].Calverton Center for Ocean-Land-Atmosphere Studies,2005:855-895.
[7]Gabriel R,Patrick F.One or Two Frequencies? The Empirical Mode Decomposition Answers[J].IEEE Transactions on Signal Processing,2008,56(1):85-96.
[8]Zheng G T,McFadden P D.A Time-Frequency Distribution for Analysis of Signals with Transient Components and Its Application to Vibration Analysis Transaction of the ASME[C]//Proc.R.Soc.London A,July 1999,2:328-333.
