基于Fisher判别的半监督天体光谱数据特征降维
2012-08-01盛英
盛 英
(太原科技大学计算机科学与技术学院,太原030024)
由于空间属性的存在,天体具有了空间位置和距离的概念,并且相邻天体之间存在一定的相互作用,天文数据之间的关系极其复杂。与其它数据相比,天文数据将以TB甚至PB计量,巨大的数据量和变化范围给分类带来很大的困难;天文数据的多波段性以及属性增加极为迅速,从如此高维的空间中提取信息、发现知识,极易引起维灾难[1]。数据降维能够把高维数据映射到较低维的空间,并且保存原始数据的绝大部分信息,有利于天体光谱数据的分类、聚类、可视化等。
目前,依据有无标号信息,天体光谱数据降维主要分两类:监督降维和无监督降维。其中典型的无监督降维工作有:覃冬梅、胡占义等提出一种基于主分量分析的恒星光谱快速分类法,通过PCA方法提取恒星光谱的主要主分量,得到降维后的样本特征点,实现了最近邻分类器的快速准确分类[2];张怀福等利用小波包提取光谱特征,研究了活动天体和非活动天体光谱的分类[3];段福庆等提出了基于Bayes决策的光谱分类,在PCA特征提取的基础上,利用Bsyes决策实现光谱分类[4];姜斌等提出了基于二维主分量分析的光谱数据降维方法[5]。总之,以PCA、小波变换等为代表的无监督降维不足之处是没有考虑训练样本中的标号信息,仅仅在指定特征向量个数的前提下,实现对原始数据的最大近似。典型的监督降维工作有:赵梅芳等提出了基于K近邻方法的窄线与宽线活动星系核的自动光谱分类,首先根据给定的红移,将光谱移回静止状态,然后根据窄线星系核和宽线星系核分类相关的特征谱线知识,截取流量,可看作一个有监督特征提取的过程[6];李乡儒等提出了RVM有监督特征提取与Seyfert光谱分类[7],能有效的利用已有的对问题的信念、先验知识、训练数据和相应的类别信息,证明了对恒星光谱数据进行监督降维分析的可行性;李乡儒、胡占义等运用Fisher判别分析法对光谱数据进行有监督特征提取[8],有效的融合了训练数据的类别信息,具有突出的维数约简能力,进一步明确了对恒星光谱数据进行监督降维的优势。总之,以RVM和Fisher判别分析为代表的监督降维,局限于只利用了一部分标号信息,降维的结果过分拟合于标号数据。另外,在现实世界中,天体光谱数据的标号信息很难获得,这时传统的监督降维将不能实行,而无标号光谱数据获得较容易,但标号信息选择将在很大程度上影响降维的效果。
分类是天体光谱数据分析与处理中的重要研究内容之一,由于天体光谱具有高维海量等特点,因此降维是提高天体光谱数据自动分类效果的有效手段之一。本文针对天体光谱数据无监督降维未考虑样本数据的类别信息,有监督降维过分拟合,以及光谱数据标号数据选择困难的不足,采用Fisher判别分析处理标号数据的有监督性和PCA处理全局数据的无监督性为启发,给出了一种基于Fisher判别分析的半监督光谱数据降维方法。该方法首先在样本数据中随机选取一部分作为标号数据,另一部分作为无标号数据,并且引入数据对、最近邻数据的处理,有效的克服了标号数据选择的困难;其次采用Fisher判别分析和PCA可变动选择的半监督降维,解决了降维过分拟合于标号数据和未考虑数据的类别信息的不足,同时克服了标号数据选择的盲目性;最后,实验证实了算法的有效性。
1 相关概念
数据降维指通过非线性或线性映射,将数据从高维投影到低维空间,获得高维数据的一个有意义的低维表示的过程[9]。设存在函数:Z=WTx,其中各参数的定义如下:Z∈Rr(1≤r≤d)W是进行线性数据降维时用的转置矩阵,T代表矩阵转置,xi∈Rd(1,2…,n)是 d维的样本向量,X ∈ Rd×n且 X=(x1∣x2∣xn)是所有样本数据构成的矩阵,Z是高维数据的低维表示[10],也是实现大量复杂数据分析的最终目标。
数据降维的过程中,通常涉及一系列的优化问题,对其中的一种形式分析即:
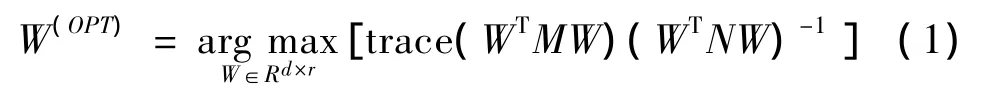
在公式(1)中,M代表尽量增加的部分,N代表尽量减小的部分,目标是实现W(OPT)的最大化。若是广义特征值是广义特征值对应的特征向量,公式(1)变为Mφ=λNφ.广义特征向量满足正交性,即,此时广义特征值按降序排列,可得到λ1≥λ2≥λ3≥…≥λd,并且广义特征向量满足标准化,既φTkNφk=1(k=1,2…,d)。所以 W(OPT)最优化问题可通过(φ1|φ2|… |φr))解决[11],常用公式(2)表示
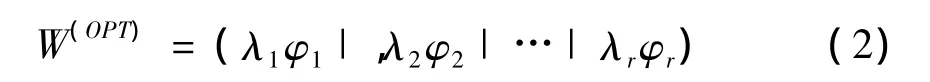
面对数据降维问题时,经常需根据数据的潜在结构特点,成对地处理,因为数据对能清楚表明数据之间的关系,例如靠近或者远离,更重要的是数据对能保持样本数据的局部结构[12],设Q是n×n的矩阵,F是n×n的对角矩阵,公式表示如下:
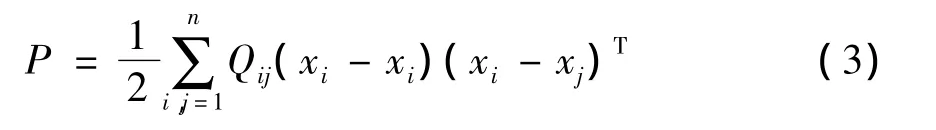
PCA是建立在K-L变换的基础上,采用大本征值对应的本征向量构成变换矩阵,保留样本数据中方差最大的数据分量,主要目标是把很多变量转换成较少的几个变量[13]。如果用数据成对表达式(3)描述PCA的降维过程,可表示为[14]:
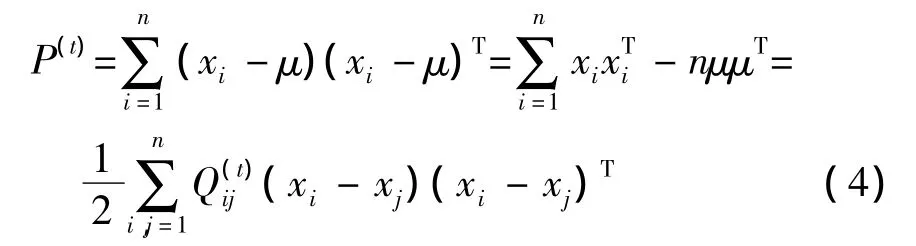
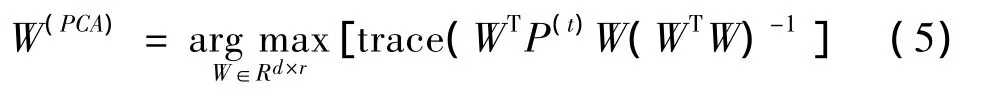
PCA是一个较好的数据降维方法,它能保持数据的全局性能,但它是一种无监督的降维算法,不能有效的利用样本数据的标号信息。
Fisher判别分析(FDA)是一个非常流行的监督降维方法,主要思想:数据类内的距离尽量很小,同时数据类间的距离尽量很大[15]。利用式(1)的思想,FDA可变成求矩阵最优化的形式[16]即:
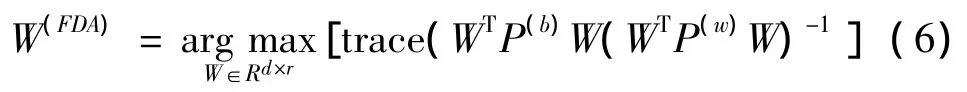
2 基于Fisher判别分析半监督降维思想
当缺乏标号信息时,传统的监督方法很难运行,然而在现实世界中,标号数据很难获取或者获取代价昂贵。直接采用半监督降维时,按照随机的方式选定标号和无标号信息,但这个方具有盲目性,有时恰巧选到不适宜进行标号的数据,使得数据降维的结果可能最坏。本文利用近邻数据的关系,降低半监督降维时由于随机的方式带来的盲目性。
近邻数据的一个重要假设是“近邻数据最有可能属于相同的类”,于是定义A是n×n的矩阵,使它能够抑制任何最近邻的数据在潜在的低维空间分离。常用的近邻数据处理方法有热核和高斯函数等,但较简单和常用的是把最近邻数据定义在热核上[18],每一对数据依据它们之间相似性做相应的惩罚,相似性依据输入数据中的数据对间的欧式距离建立,既,公式中字母σ是十分重要的变量,因为它控制着矩阵A缩放的范围和幅度,更重要的是它影响着总体数据的分类数目和效果。进一步假设σi代表xi与它周围的其它点接近程度,k代表xi最邻点的个数,此时有其中Aij表示xi和xj的距离远近关系[19],取值范围介于0和1之间,若xi和xj之间的距离足够大,Aij的取值十分接近0,相反若xi和xj之间的距离足够小,Aij的值就接近1.论文中,降维时Aij处理的数据对属于相同类中的标号数据,当用Aij降低随机选择标号信息的影响时,FDA的最优化公式中P(b)和P(w)可分别用数据对权值思想表示既:若yi=yj,则:
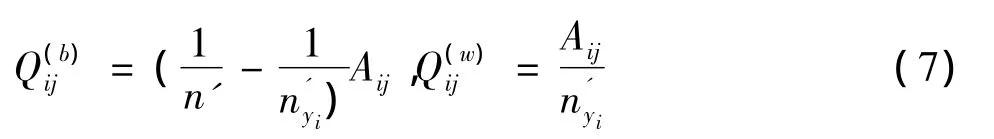
基于数据降维理论(5)和(6),提出一种基于FDA的半监督光谱数据降维方法。由于FDA虽然能有效的利用标号信息,但监督性使得降维结果往往过分拟于标号数据,而无标号数据能很好的调和这个问题,另外PCA作为无监督降维方法,能够很好的保持整个数据的结构。在式(1)求解广义特征值的基础上,假设P(rb)为正规化的类间矩阵,P(rw)为正规化的类内矩阵,可求出整个广义特征值即:

为了利用标号信息的同时也能利用无标号信息,实现半监督降维性能,对公式变量做要求:
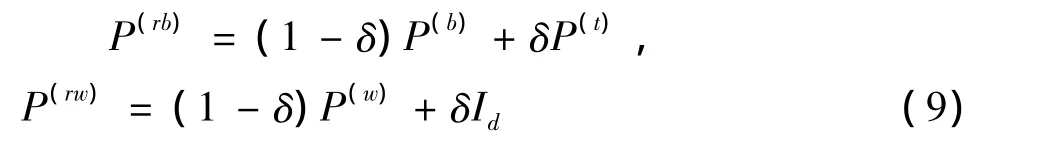
字母δ是变量,取值范围从0到1,它的变化使P(rb)φ =λP(rw)φ,求解偏重在FDA和PCA间滑动,论文将根据光谱数据的特点,分析δ的取值。基于数据成对表达在数据降维中的广泛应用,论文在数据成对表达的基础上,找到一个转换矩阵W,这个矩阵W满足:在样本数据的潜在空间,类内之间的距离尽量最小,同时使类间的距离尽量最大即:
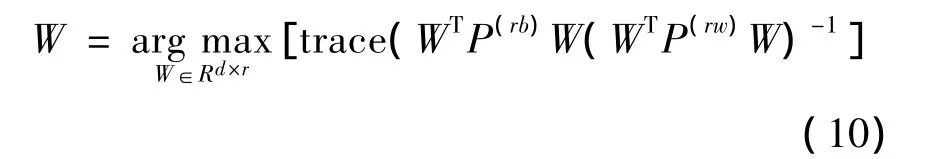
可看出此公式与前面的FDA和PCA变化形式很相似,若用{λk}dk=1表示最优化求出的特征值,{φk}dk=1表示与特征值对应的特征向量,降维的问题可通过转置矩阵得到即:
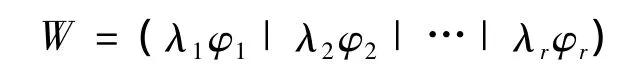
针对光谱数据无监督降维不能利用标号信息,只是在特征向量个数一定的条件下,实现对原始数据空间最大近似,监督降维过分拟合于标号数据,采用可调节参数δ的半监督降维,降低了单独的监督或无监督降维的不足,同时δ弥补了标号数据选择的随机性。原始样本数据总共有n个,其中有n'个带有标号的数据,剩余的(n-n')个为无标号数据,若yi是在样本xi中的标号数据,用公式可以表示成形式且 yi∈ {1,2…,c},c是类的数目,d是原始数据的维数,r是降维后维数。算法步骤可表述如下:
输出:(d×r)的转置矩阵W
2)若 yi=yj,则,否则
3)求出P(b)和P(w);
4)用 P(rb)=(1- δ)P(b)+ δP(t),P(rw)=(1-δ)P(w)+ δId,求 P(rb)和 P(rw);
5)用P(rb)φ=λP(rw)φ特征值和特征向量的关系,求 W=(λ1φ1| λ2φ2… | λrφr)。
在上述算法中,Aij抑制任何最近邻的数据在潜在的低维空间分离,处理属于相同类中的标号数据,克服了标号信息选择的盲目性带来的影响,有利于半监督数据降维分析;系数δ巧妙的把监督FDA和无监督PCA结合起来,通过广义特征值的思想,求出光谱数据的主要成分构成的矩阵,找到光谱数据潜在低维空间,克服了监督降维过分拟合于标号数据,无监督降维未考虑类别信息的不足,同时不断变化的δ最大的利用了FDA和PCA的优势,使光谱数据降维的损失尽量达到最小;字母δ是变量,取值范围从 0到 1,它的变化使 P(rb)φ =λP(rw)φ,求解偏重在FDA和PCA间滑动,当δ=0时,公式变成FDA,当δ=1时,公式变成PCA,文章中为了分析δ取值对半监督降维的影响,依次取δ的值为 0,0.1,0.3,0.5,0.7,0.9 和 1.通过分类正确率的提高得到验证。
3 实验结果分析
实验环境:Pentium D925 CPU,512内存,Windows XP操作系统,采用 MATLAB7.1实现 FDA、PCA和半监督降维算法。利用K近邻分类器评价降维效果,因为它在很多的数据集分类中表现较好,是一个常用的、相对简单的分类方法[19],实验中k的值取为1.
实验数据是国家天文台提供的高红移类星体、晚型星两个SDSS天体光谱数据集,其中44条光谱特征线作为属性,既维数为44,光谱数据分别含有5403条(7 M)、34117条(46 M),把全部的高红移类星体和晚型星合并为原始样本数据集合。首先取原始样本数据集合条数的2/3作为训练数据集,剩下的1/3作为测试集;其次随机选取训练集总条数的0.2 倍、0.4 倍、0.6 倍、0.8 倍作为标号数据,训练集的其余数据作为无标号数据,按照本篇文章的方法进行半监督降维;最后利用1最近邻分类法来计算测试集的正确分类率。实验重复十次,每次都随机选取样本数目的2/3作训练数据集,剩余是测试集,计算降维方法的平均正确分类率。半监督降维系数 δ的取值是 0,0.1,0.3,0.5,0.7,0.9,1.
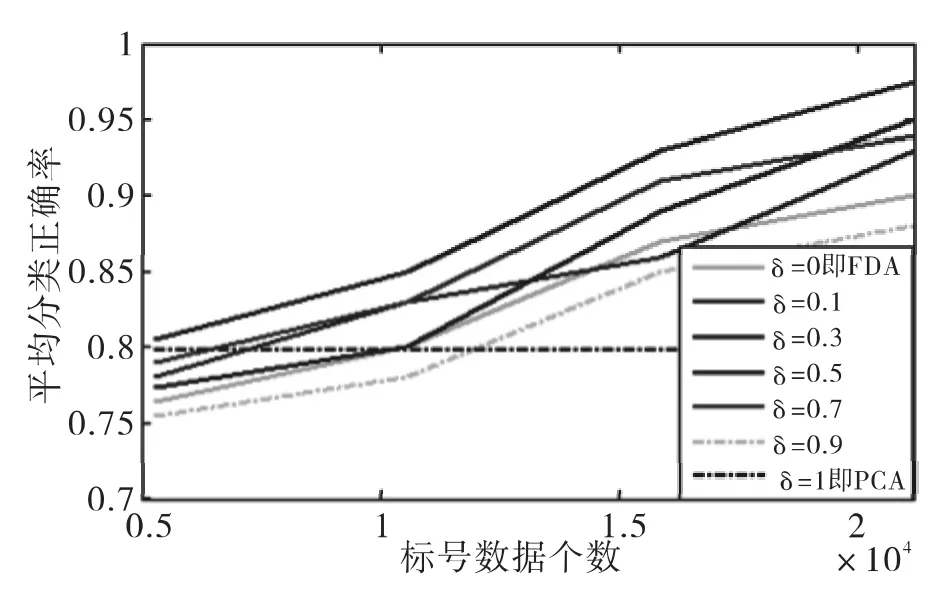
图1 降维效果Fig.1 The effect of dimensionality reduction
由图1可知:1)由于FDA半监督降维算法,采用有监督思想有效地利用了光谱数据中的类别信息,同时利用无监督的PCA保持了光谱数据的全局性能,所以FDA半监督方法与PCA、FDA相比较,降维后平均分类正确率一般很高;2)不同的δ有可能避免FDA和PCA的大部分缺点,所以平均正确分类率有所差别,甚至相差很大;3)因为标号数据可以提供类别信息,故标号数据数越多,降维后的平均分类正确率越高;4)由于PCA是无监督的降维算法,PCA降维后分类的结果不受标号数据个数选择的影响。
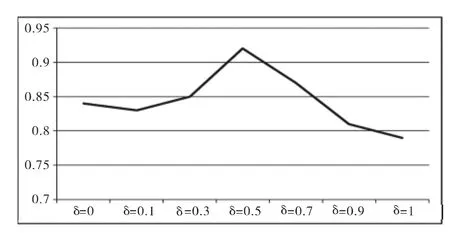
图2 对平均正确分类率影响Fig.2 Impact on the average correct classification rate
标号数据的个数取值为1.5×104,分析δ对平均分类正确率的影响,从图2可以看出,(1)δ=0.5时,实验的分类正确率最高,因为0.5处于半监督降维结合的中间位置,可能最大利用了PCA和FDA的优势;(2)δ从0到1变化时,分类正确率并没有单调减小或单调增加,这说明光谱数据不但具有高维海量的特性,而且及其复杂。
4 结束语
针对光谱数据监督和无监督降维的缺陷,本文给用了一种基于Fisher判别分析的半监督降维方法。采用光谱数据集,并利用平均分类正确率作为降维效果的比较标准,实验验证了该方法的可行性和良好的降维效果。
[1]张继福,蔡江辉.面向LAMOST的天体光谱离群数据挖掘系统研究[J].光谱学与光谱分析,2007,27(3):606-607.
[2]覃冬梅,胡占义,赵永恒.一种基于主分量分析的恒星光谱快速分类法[J].光谱学与光谱分析,2003,23(1):182-182.
[3]张怀福.小波在LAMOST光谱处理中的应用[D].北京:北京交通大学,2008.
[4]刘蓉,勒红梅,段福庆.基于Bayes决策的光谱分类[J].光谱学与光谱分析,2010,30(3):838-839.
[5]姜斌,潘景昌,郭强,等.基于二维主分量分析的光谱数据降维方法[J].现代电子技术,2007,14(21):21-22.
[6]赵梅芳,吴潮.基于K近邻方法的窄线与宽线活动星系核的自动光谱分类[J].天文学报,2007,48(1):1-2.
[7]李乡儒,胡占义,赵永恒,等.RVM有监督特征提取与Seyfert光谱分类[J].光谱学与光谱学分析,2009,29(6):1702-1703.
[8]李乡儒,胡占义,赵永恒.基于Fisher判别分析的有监督特征提取和星系分类[J].光谱学与光谱分析,2007,27(9):1888-1889.
[9]宋欣,叶世伟.基于直接估计梯度思想的数据降维算法[J].计算机工程,2008,34(8):205-205.
[10]谭璐.高维数据的降维理论及应用[D].长沙:国防科技大学,2005.
[11]FUKUNAGA K.Introduction to statistical pattern recognition(2nd ed)[D].San Diego:Academic Press,1990.
[12]BELKIN M,NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation,2003,15:1373-1396.
[13]吴晓婷,闫德勤.数据降维方法分析与研究[J].计算机应用与研究,2009,26(8):2832-2833.
[14]CHEN Guangyi.Denoising and dimensionality reduction of hypersepectral imagery using wavelet packets,neighbour shrinking and principal component analysis[J].International Journal of Remote Sensing,2009,30(18):4889-4890.
[15]赵玲玲.半监督降维和分类算法研究[D].西安电子科技大学,2009.
[16]杜世强.基于核Fisher判别的人脸识别方法研究[D].陕西师范大学,2007.
[17]ZHA H Y,ZHANG ZH Y.Spectral properties of the alignment matrices in manifold learning[J].SIAM Review,2009,51:545-565.
[18]CHAPELLE O,SCHOLKOPF B,ZIEN A,Semi-supervised Learning[M].US:MA,The MIT Press,2006.
[19]ZELNIK-MANOR L,PERONA P.Self-tuning spectral clustering[J].NIPS,2004,17:1601-1608.
