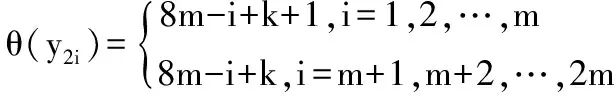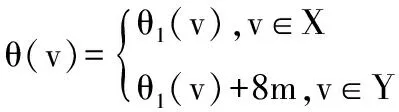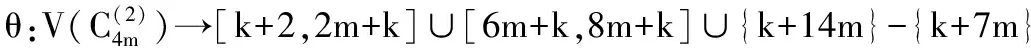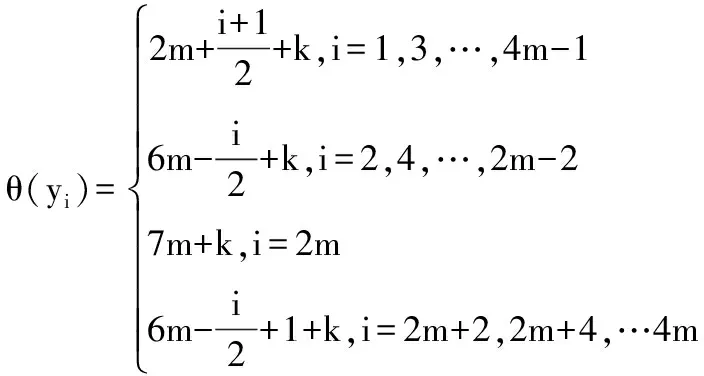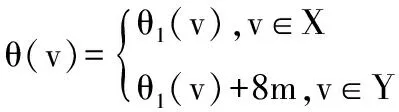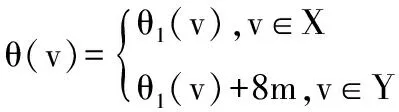非连通图2C4m∪G是优美图的5个充分条件
2015-06-23吴跃生
吴跃生
(华东交通大学 理学院,南昌 330013)
非连通图2C4m∪G是优美图的5个充分条件
吴跃生
(华东交通大学 理学院,南昌 330013)
讨论了非连通图2C4m∪G的优美性,给出了非连通图2C4m∪G是优美图的5个充分条件。
优美图;交错图;非连通图;优美标号
1 相关概念
图的优美标号问题是组合数学中的一个热门课题。
定义1[1]对于一个图G=(V,E),如果存在一个单射θ:V(G)→[0,|E(G)|]使得对所有边e=(u,v)∈E(G),由θ′(e)=|θ(u)-θ(v)|导出的映射θ′:E(G)→[1,|E(G)|]是一一对应的,则称G是优美图,θ是G的一组优美标号。

本文所讨论的图均为无向简单图,V(G)和E(G)分别表示图G的顶点集和边集。记号Gk+m表示图G是特征为k且缺k+m标号值的交错图。记号[m,n]表示整数集合{m,m+1,…,n},其中m和n均为非负整数,且满足0≤m 文献[1]已经证明了非连通图2C4m是优美图。文献[2]研究了非连通图2C4m∪Cn的优美性,证明了非连通图2C4m∪C8m-1,2C4(3m-1)∪C8m-1和2C4(3m+1)∪C4(2m+1)是优美图。文献[3]讨论了非连通图2C4m∪G的优美性,给出了非连通图2C4m∪G是优美图的一个充分条件:对任意正整数m,设G是特征为k,且缺k+2m+1标号值的交错图,则非连通图2C4m∪G存在特征为4m+k+1,且缺k+1标号值的交错标号(2m+1≤k+2m+1≤|E(G)|)。 本文继续讨论非连通图2C4m∪G的优美性,给出非连通图2C4m∪G的是优美图的五个充分条件。 定理1 对任意正整数m,如果2m≤k+2m≤|E(G)|,则非连通图2C4m∪Gk+2m存在特征为4m+k,且缺k+8m标号值的交错标号。 把非连通图2C4m∪Gk+2m的顶点标号θ定义为: θ(x2i)=2m+i+k+1,i=1,2,…,m-1; θ(x2m)=m+k+1,θ(x2i)=2m+i+k,i=m+1,m+2,…,2m; θ(x2i-1)=6m-i+k+1,i=1,2,…,2m; θ(y2i-1)=8m-i+k,i=1,2,…,2m-1; θ(y4m-1)=k+10m。 θ:X→[0,k]是单射(或双射);θ:Y→[k+8m+1,q+8m]-{k+10m}是单射; 因而,映射θ:V(2C4m∪Gk+2m)→[0,q+8m]-{k+8m}是单射。 θ′(x2m-1x2m)=4m, θ′(x2mx2m+1)=4m-1,θ′(x4mx1)=2m, θ′(y4m-1y4m)=8m-1, θ′(y4m-2y4m-1)=8m,θ′(y4my1)=6m-2, θ′:E(Gk+2m)→[8m+1,q+8m]是双射。 因而,映射θ′:E(2C4m∪Gk+2m)→[1,q+8m]一一对应,所以θ就是非连通图2C4m∪Gk+2m的缺k+8m标号值的优美标号。 所以,θ就是非连通图2C4m∪Gk+2m的特征为4m+k,且缺k+8m标号值的交错标号。证毕。 定理2 对任意正整数m,如果6m-1≤k+6m-1≤|E(G)|,则非连通图2C4m∪Gk+6m-1存在缺k+8m标号值的优美标号。 定义非连通图2C4m∪Gk+6m-1的顶点标号θ为: θ(x2i)=6m-i+k-1,i=1,2,…,m-1; θ(x2m)=7m+k-1, θ(x2i)=6m-i+k,i=m+1,m+2,…,2m; θ(x2i-1)=2m+i+k-1,i=1,2,…,2m; θ(y2i-1)=i+k,i=1,2,…,2m-1; θ(y4m-1)=k+14m-1。 顺应论视角下的美剧字幕翻 译 ………………………………………………………………………… 安 红(62) θ:X→[0,k]是单射(或双射);θ:Y→[k+8m+1,q+8m]-{k+14m-1}是单射; 因而,映射θ:V(2C4m∪Gk+6m-1)→[0,q+8m]-{k+8m}是单射。 θ′:E(Gk+6m-1)→[8m+1,q+8m]是双射。 因而,映射θ′:E(2C4m∪Gk+6m-1)→[1,q+8m]一一对应,θ就是非连通图2C4m∪Gk+6m-1的缺k+8m标号值的优美标号。 定理3 对任意正整数m,如果6m≤k+6m≤|E(G)|,则非连通图2C4m∪Gk+6m存在缺k+1标号值的优美标号。 定义非连通图2C4m∪Gk+6m的顶点标号θ为: θ(x2i)=6m-i+k,i=1,2,…,m-1; θ(x2m)=7m+k, θ(x2i)=6m-i+k+1,i=m+1,m+2,…,2m; θ(x2i-1)=2m+i+k,i=1,2,…,2m; θ(y2i-1)=i+k+1,i=1,2,…,2m-1; θ(y4m-1)=k+14m。 θ:X→[0,k]是单射(或双射);θ:Y→[k+8m+1,q+8m]-{k+14m}是单射; 因而,映射θ:V(2C4m∪Gk+6m)→[0,q+8m]-{k+1}是单射。 θ′:E(Gk+6m)→[8m+1,q+8m]是双射。 因而,映射θ′:E(2C4m∪Gk+6m)→[1,q+8m]一一对应,θ就是非连通图2C4m∪Gk+6m的缺k+1标号值的优美标号。 定理4 对任意正整数m,如果6m≤k+6m≤|E(G)|,则非连通图2C4m∪Gk+6m存在缺k+2m标号值的优美标号。 定义非连通图2C4m∪Gk+6m的顶点标号θ为: θ:X→[0,k]是单射(或双射);θ:Y→[k+8m+1,q+8m]-{k+14m}是单射。 因而,映射θ:V(2C4m∪Gk+6m)→[0,q+8m]-{k+2m}是单射。 θ′:E(Gk+6m)→[8m+1,q+8m]是双射。 因而,映射θ′:E(2C4m∪Gk+6m)→[1,q+8m]一一对应,θ就是非连通图2C4m∪Gk+6m的缺k+2m标号值的优美标号。 定理5 对任意正整数m,如果6m+1≤k+6m+1≤|E(G)|,则非连通图2C4m∪Gk+6m+1存在缺k+6m标号值的优美标号。 定义非连通图2C4m∪Gk+6m+1的顶点标号θ为: θ:X→[0,k]是单射(或双射);θ:Y→[k+8m+1,q+8m]-{k+14m+1}是单射; 因而,映射θ:V(2C4m∪Gk+6m+1)→[0,q+8m]-{k+6m}是单射。 θ′:E(Gk+6m+1)→[8m+1,q+8m]是双射。 因而,映射θ′:E(2C4m∪Gk+6m+1)→[1,q+8m]一一对应,θ就是非连通图2C4m∪Gk+6m+1的缺k+6m标号值的优美标号。 引理1[3]圈c4n存在特征为2n-1,且缺3n的交错标号。 注意到:3n=(2n-1)+n+1,由定理1和引理1有以下推论。 推论1 对任意正整数m,非连通图2C4m∪C8m-4存在特征为8m-3且缺12m-3标号值的交错标号。 例1 当m=2时,非连通图2C8∪C12的特征为13且缺21标号值的交错标号为: 20,6,19,7,18,9,25,10; 17,11,16,8,15,12,14,13; 0,28,1,27,2,26,3,24,4,23,5,22。 注意到:12m-3=(8m-3)+4m,由定理和推论1有如下推论。 推论2 对任意正整数m,非连通图2C8m∪(2C4m∪C8m-4)存在特征为16m-3且缺24m-3标号值的交错标号。 例2 当m=4时,非连通图2C16∪(2C8∪C12)的特征为29且缺45标号值的交错标号为: 37,23,36,24,35,25,34,18,33,26,32,27,31,28,30,29; 44,14,43,15,42,16,41,17,40,19,39,20,38,21,53,22; 52,6,51,7,50,9,57,10; 49,11,48,8,47,12,46,13; 0,60,1,59,2,58,3,56,4,55,5,54。 注意到:24m-3=(16m-3)+8m,由定理1和推论2有如下推论。 推论3 对任意正整数m,非连通图2C16m∪(2C8m∪(2C4m∪C8m-4))存在特征为32m-3且缺48m-3标号值的交错标号。 注意到:48m-3=(32m-3)+16m,由定理1和推论3有如下推论。 推论4 对任意正整数m,非连通图2C32m∪(2C16m∪(2C8m∪(2C4m∪C8m-4)))存在特征为64m-3且缺96m-3标号值的交错标号。 重复上述过程,可以构造出许多交错图。 注意到:3n=(2n-1)+n+1,由定理2和引理1有如下推论。 推论5 对任意正整数m,非连通图2C4m∪C24m-8存在缺20m-5标号值的优美标号。 例3 当m=2时,非连通图2C8∪C40缺35标号值的优美标号为: 23,29,24,32,25,28,26,27; 20,34,21,33,22,31,46,30 0,56,1,55,2,54,3,53,4,52,5,51,6,50,7,49,8,48,9,47,10,45,11,44,12,43,13,42,14,41,15,40,16,39,17,38,18,37,19,36。 注意到:3n=(2n-1)+n+1,由定理3和引理1有如下推论。 推论6 对任意正整数m,非连通图2C4m∪C24m-4存在缺12m-2标号值的优美标号。 例4 当m=2时,非连通图2C8∪C44缺22标号值的优美标号为: 26,32,27,35,28,31,29,30; 23,37,24,36,25,34,49,33 0,60,1,59,2,58,3,57,4,56,5,55,6,54,7,53,8,52,9,51,10,50,11,48,12,47,13,46,14,45,15,44,16,43,17,42,18,41,19,40,20,39,21,38。 注意到:3n=(2n-1)+n+1,由定理4和引理1有如下推论。 推论7 对任意正整数m,非连通图2C4m∪C24m-4存在缺14m-3标号值的优美标号。 例5 当m=2时,非连通图2C8∪C44缺25标号值的优美标号为: 37,22,36,23,34,24,33,49; 26,32,27,35,28,31,29,30; 0,60,1,59,2,58,3,57,4,56,5,55,6,54,7,53,8,52,9,51,10,50,11,48,12,47,13,46,14,45,15,44,16,43,17,42,18,41,19,40,20,39,21,38。 注意到:3n=(2n-1)+n+1,由定理5和引理1有如下推论。 推论8 对任意正整数m,非连通图2C4m∪C24m存在缺18m-1标号值的优美标号。 例6 当m=2时,非连通图2C8∪C48缺35标号值的优美标号为: 39,24,38,26,37,27,36,52; 34,28,33,25,32,29,31,30; 0,64,1,63,2,62,3,61,4,60,5,59,6,58,7,57,8,56,9,55,10,54,11,53,12,51,13,50,14,49,15,48,16,47,17,46,18,45,19,44,20,43,21,42,22,41,23,40。 [1] 马克杰.优美图[M].北京:北京大学出版社,1991. [2] 董俊超.C4k∪C4k∪Cm的优美性[J].烟台大学学报:自然科学与工程版,1999,12(4):238-241. [3] 吴跃生,王广富,徐保根.非连通图2C4m∪G的优美标号[J].烟台大学学报:自然科学与工程版,2014,27(4):240-243. (责任编校:夏玉玲) On Five Sufficient Conditions for the Gracefulness of Unconnected Graph 2C4m∪G WU Yue-sheng (School of Science, East China Jiaotong University, Nanchang 330013,China ) The author of this paper discusses the gracefulness of the unconnected graph 2C4m∪Gand puts forward five sufficient conditions for the gracefulness of the unconnected graph. graceful graph;alternative graph; unconnected graph; graceful labeling O157.5 A 1672-349X(2015)03-0004-04 10.16160/j.cnki.tsxyxb.2015.03.0022 主要结论及其证明