多空位缺陷和硼氮杂质对锯齿型石墨烯纳米带电子结构的影响

肖建田，胡大胜，陈灵娜, ，吴取劲，李丽华

(1.南华大学 计算机科学与技术学院，湖南 衡阳，421001；2.长沙师范学校，湖南 长沙，410100；3.中南大学 信息科学与工程学院，湖南 长沙，410083)

近年来，石墨烯纳米带[1-5]作为新型的一维碳基纳米材料，引起了人们的广泛关注。特别是锯齿型(zigzag)石墨烯纳米带[6-7]由于其自身独特的几何结构和电子性质，在应用方面更具有潜力。在实验制备过程中，石墨烯纳米带中可能会引入杂质和缺陷。杂质和缺陷对石墨烯纳米带的电子结构会有很大影响，但是到目前为止，具体的关系并不十分明确，因此值得深入研究。最近，石墨烯纳米带的半金属和半导体性引起了人们的研究兴趣[8-11]，这是因为半金属性在未来的自旋电子学领域中有广泛的应用前景，如自旋阀[12]、自旋二极管[13]、自旋场效应管[14]等。半金属性纳米材料的理论研究是一项非常重要的研究工作。但是，人们对石墨烯纳米带半金属性的研究仍然很少。大量的实验和理论证明石墨烯纳米带中普遍存在着各种各样的缺陷，常见的缺陷是空位缺陷[15-16]和拓扑缺陷[17-18]。石墨烯纳米带的电子结构对缺陷构型和杂质类型都很敏感。以前的研究主要集中在石墨烯纳米带中的单空位缺陷和拓扑缺陷。尽管石墨烯纳米带中缺陷和掺杂效应已经取得了一些进展，但目前仍存在一些亟待解决的问题。在此，本文作者通过第一性原理计算，研究了zigzag石墨烯纳米带(ZGNR)的电子结构。计算结果显示，在石墨烯纳米带的锯齿形边缘上存在自旋极化的边缘电子态，并且边缘上的电子自旋呈反铁磁性排列。多空位缺陷和硼氮杂质可以诱导zigzag石墨烯纳米带具有不同的电子结构。因此，石墨烯纳米带在自旋过滤器等纳米电子器件中有很大的应用前景。

1 计算模型和方法

为了研究缺陷和杂质对锯齿型(zigzag)石墨烯纳米带电子结构的影响，需要选定一定宽度和长度的石墨烯纳米带作为原胞，在原胞中间去掉几个碳原子形成多空位缺陷或硼氮原子替代掺杂。宽度和长度的选择要保证石墨烯纳米带边缘处的结构以及2个空位缺陷之间的石墨烯纳米带结构不能发生明显的变化。由于氢原子对边缘的饱和会导致边缘电子态的自发自旋极化消失，从而导致半金属性的消失。因此zigzag石墨烯纳米带的边缘不用氢原子饱和。图1所示为8-ZGNR的超胞构型。其中：M1为完整的8-ZGNR构型；M2为多空位缺陷的8-ZGNR构型；M3为6个氮原子掺杂的8-ZGNR构型；M4为6个硼原子掺杂的8-ZGNR构型。这4个构型中缺陷和掺杂位置都是M1模型中的字母A～F标记位点。

zigzag石墨烯纳米带的几何结构优化和电子结构的计算都是采用基于密度泛函理论[19-20]的VASP程序包完成的。采用了投影缀加波方法[21]，并且选择了广义梯度近似(GGA)和Perdew-Wang 91(PW91)交换关联函数[22-24]。平面基组的截断能是400 eV。为了避免石墨烯纳米带之间的相互作用，zigzag石墨烯纳米带之间的真空层选取为1 nm。在进行优化和计算中，一维的简约布里渊区积分通过Monkhost-Pack 方法自动产生，k点取样是一个1×1×11的网格。结构弛豫收敛判据设为每个原子受力小于0.1 eV/nm。计算能带时，本文按照Line模式产生K点，k点取样是一个1×1×21的网格。

图1 8-ZGNR的超胞构型Fig.1 Supercell configuration of 8-ZGNR

2 结果和讨论

研究了石墨烯纳米带的多空位缺陷和硼氮单独掺杂构型的电子结构，且缺陷和掺杂都是在相同的位点。图2所示为完整的、多空位缺陷和硼氮单独掺杂的8-ZGNR的能带结构图，虚线和实线分别表示自旋向上和自旋向下的能带。从图2(a)可见：宽度为8的完整的zigzag石墨烯纳米带的能带结构中费米能级附近的自旋能带发生了分裂。2个自旋中都有1条对应于边缘态的能带与费米能级相交。在完整的zigzag石墨烯纳米带中，2条边缘态的能带属于左右边缘共有，两边的碳原子对它们都有影响。因此，完整的8-ZGNR显示为金属性质。当M1构型中A～F 6个碳原子全部去除得到了多空位缺陷M2构型，且缺陷的边缘则不用氢饱和。M2构型的能带结构如图2(b)所示，自旋向上的能带中出现2条局域化能带与费米能级相交，则自旋向上的能带为金属性质。然而自旋向下的能带在费米能级附近出现了较宽的能隙，能隙约为0.340 eV，则多空位缺陷造成了自旋向下的能带变成了半导体特性。因此，M2的能带结构特征表明具有多空位缺陷的8-ZGNR显示了半金属性质。由于边缘态是局域态，它属于处于边缘的碳原子，而多空位缺陷位于石墨烯纳米带的中间，因此它不会使边缘态消失。2个自旋在费米能级附近较为平坦的能带是空位缺陷引入了的局域态，是空位缺陷周围具有悬挂键的碳原子带来的局域态。图2(c)所示为M3的能带结构图，自旋向上的能带中出现了约为0.509 eV能隙，而自旋向下的能带中有多条局域态交于费米能级。因此，M3体系同样显示了半金属特性，这是由于氮杂质向系统中注入了多余的电子，这些电子在费米能级附近产生了局域态。从图2(d)可以发现：M4体系的自旋向上和自旋向下的能带都产生较宽的能隙，自旋向上的能隙约为0.403 eV，而自旋向下的能隙约为0.596 eV。因此，硼掺杂使得8-ZGNR具有半导体性质，这是因为硼杂质引入了多余空穴，导致了局域杂质态强烈影响了2个自旋费米能级附近的π/π*状态。计算结果表明，多空位缺陷或硼氮单独掺杂可以诱导zigzag石墨烯纳米带呈现半金属或半导体特性，其物理原因在于zigzag石墨烯纳米带超胞长度较小，导致相邻缺陷或杂质之间存在着长程相互作用，缺陷态、杂质态以及边缘态强烈地影响了费米能级附近的 π/π*状态。

M1，M2，M3和M4这4个体系的总态密度(DOS)如图3所示。态密度图揭露了费米能级附近的峰主要由原子的pz轨道贡献。完整的8-ZGNR的态密度图中显示了2个自旋都没有能隙，并且2个自旋的态密度峰在费米能级处都比较平缓，如图3(a)所示。当完整的8-ZGNR中出现多空位缺陷时，自旋向下的态出现了较宽的态密度谷，而自旋向上的较低态密度峰与费米能级相交，如图3(b)所示。从图3(c)可以发现：自旋向上的态出现了态密度谷，而自旋向下的较高态密度峰与费米能级相交。与M1体系的电子结构不同，硼掺杂导致M4体系中2个自旋在费米能级处都出现了态密度谷，如图3(d)所示。计算结果表明：多空位缺陷和硼氮杂质强烈地影响了8-ZGNR费米能级附近的电子结构。

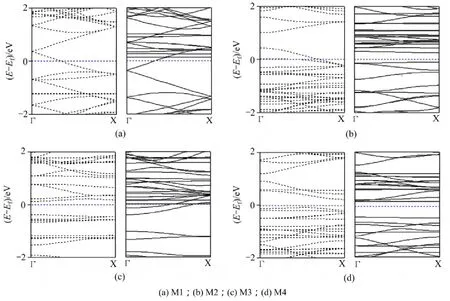
图2 具有多空位缺陷或硼氮掺杂的8-ZGNR能带结构Fig.2 Energy band structure of 8-ZGNR with multivacancies defect or B/N doping

图3 具有空位缺陷或硼氮掺杂的8-ZGNR的态密度(DOS)Fig.3 Density of states of 8-ZGNR with multivacancies defect or B/N doping

基态状态下8-ZGNR自旋态密度分布如图4所示。从图4(a)可知：完整的8-ZGNR自旋态密度主要局域分布在带边缘上，且边缘上的自旋相互之间是反铁磁性耦合，导致每个超胞内7.390 μB(μB为波尔磁子)磁矩。从图4(b)中观察到多空位缺陷处出现了自旋态密度分布，从而造成了每个超胞内磁矩的增加，则磁矩变为9.751 μB。如图4(c)所示，氮原子上没有出现局部自旋态密度分布，而且多余电子的注入只是造成了M3体系的磁矩微小的改变，则每个超胞内的磁矩减少到6.671 μB。尽管硼杂质向完整的8-ZGNR注入了一些空穴，但M4体系的边缘上自旋态分布几乎没有受到影响，则每个超胞内的磁矩为7.767 μB，如图4(d)所示。因此，可推断出多空位缺陷和硼氮杂质对石墨烯纳米带自旋分布影响机制不同，由空位缺陷所造成的悬挂键部分充当了自旋的载体，造成了磁矩增加。而硼氮原子的引入对体系的磁矩的影响相对较弱。

对于zigzag石墨烯纳米带，由于宽度N等于奇数或偶数，则体系具有不同的对称性，因此对于2种情况本文都进行了计算。具有多空位缺陷的N-ZGNR的宽度N与磁矩的关系如图5所示。从图5可见：具有多空位缺陷N-ZGNR的磁矩随带宽的增加而呈现震荡效应，边缘上自旋和多空位缺陷处自旋之间的相互作用强度先随距离的增加而增强，当磁矩达到了饱和后，随着带宽的继续增加，2种自旋之间的相互作用反而减弱,则磁矩减少。这是因为当带宽较小时，缺陷部分对边缘部分的影响较大，从而使得能级发生较大的分裂和磁矩增加。随着带宽的进一步增加，缺陷部分相对整体来说变小，离边缘的距离也越来越远，故对边缘部分的影响也越来越小，因此磁矩也随之减少。上述结果表明：体系的磁矩不仅强依赖于石墨烯纳米带的带宽和缺陷的构型，而且依赖于多空位缺陷与石墨烯纳米带边缘的相对位置。

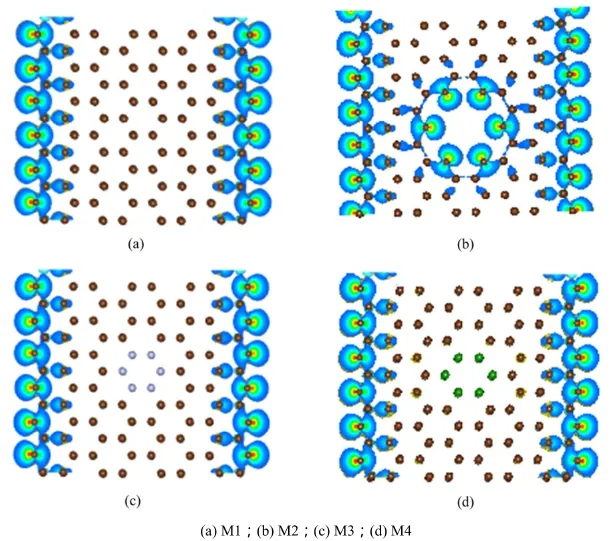
图4 具有空位缺陷或硼氮掺杂的8-ZGNR的自旋态密度投影Fig.4 Spin projected density of states of 8-ZGNR with multivacancies defect or B/N doping

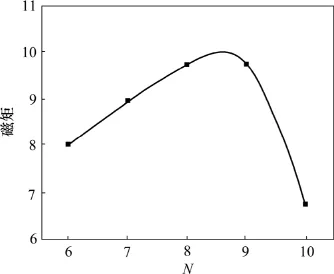
图5 具有多空位缺陷的N-ZGNR的宽度与磁矩的关系Fig.5 Relation between ribbon widths of N-ZGNR and magnetic moment

3 结论

(1)具有相同位置的多空位缺陷和氮掺杂使得对称性ZGNR呈现了半金属特性，而硼掺杂导致了对称性ZGNR显示了半导体性质。石墨烯纳米带的锯齿形边缘上和空位缺陷处都存在自旋极化的电子态，并且边缘上电子自旋呈反铁磁性排列。

(2)边缘上自旋和多空位缺陷处自旋之间的相互作用强度随着距离的增加先增强后减弱，从而导致了具有多空位缺陷的zigzag石墨烯纳米带的磁矩随带宽的增加而呈现震荡效应，并且磁矩依赖于带宽、多空位缺陷的构型以及多空位缺陷与带边缘的距离。

[1]Jiao L Y, Zhang L, Wang X R, et al.Narrow graphene nanoribbons from carbon nanotubes[J].Nature, 2009, 458 :877-880.

[2]Ritter K A, Lyding J W.The in fl uence of edge structure on the electronic properties of graphene quantum dots and nanoribbons[J].Nature Materials, 2009, 8(3): 235-242.

[3]Wang X R, Li X L, Zhang L, et al.N-doping of graphene through electrothermal reactions with ammonia[J].Science, 2009,324 : 768-771.

[4]Han M Y, Özyilmaz B, Zhang Y B, et al.Energy band-gap engineering of graphene nanoribbons[J].Phys Rev L, 2007, 98:206805.

[5]Querlio D Z, Apertet Y, Valentin A, et al.Suppression of the orientation effects on bandgap in graphene nano-ribbons in the presence of edge disorder[J].Appl Phys Lett, 2008, 92: 042108.

[6]Son Y W, Cohen M L, Louie S G, et al.Half-metallic graphene nanoribbons[J].Nature, 2006, 444: 347-349.

[7]Li Z Y, Qian H Y, Wu J, et al.Role of symmetry in the transport properties of graphene nanoribbons under bias[J].Phys Rev Lett,2008, 100: 206802.

[8]Oeiras R Y, Araújo-Moreira F M, da Silva E Z.Defect-mediated half-metal behavior in zigzag graphene nanoribbons[J].Phys Rev B, 2009, 80: 073405.

[9]Zhang Y T, Jiang H, Sun Q F, et al.Spin polarization and giant magnetoresistance effect induced by magnetization in zigzag graphene nanoribbons[J].Phys Rev B, 2010, 81: 165404.

[10]Wu M H, Wu X J, Gao Y, et al.Materials design of half-metallic graphene and graphene nanoribbons[J].Appl Phys Lett, 2009, 94:223111.

[11]Dutta S, Manna A K, Pati S K.Intrinsic half-metallicity in modi fi ed graphene nanoribbons[J].Phys Rev Lett, 2009, 102:096601.

[12]Lakshmi S, Roche S, Cuniberti G，Spin-valve effect in zigzag graphene nanoribbons by defect engineering[J].Phys Rev B,2009, 80: 193404.

[13]Krompiewski S.Spin-polarized transport in graphene nanoribbons with one paramagnetic lead and one ferromagnetic lead[J].Semicond Sci Technol, 2010, 25: 085011.

[14]Guo J, Gunlycke D, White C T.Field effect on spin-polarized transport in graphene nanoribbons[J].Appl Phys Lett, 2008,92:163109.

[15]Deretzis I, Fiori G, Iannaccone G, et al.Effects due to backscattering and pseudogap features in graphene nanoribbons with single vacancies[J].Phys Rev B, 2010, 81: 085427.

[16]Topsakai M, Aktürk E, Sevinçli H, et al.First-principles approach to monitoring the band gap and magnetic states of a graphene nanoribbon via it vacancies[J].Phys Rev B, 2008, 78:235435.

[17]Ren Y, Chen K Q.Effect of symmetry and stone-wale defect on spin-dependent electronic transport in zigzag graphane nanoribbons[J].J Appl Phys, 2010, 107: 044514.

[18]Bhownick S, Waghmare U V.Anisotropy of the stone-wales defect and warping of graphene nanoribbons: A first-principles analysis[J].Phys Rev B, 2010, 81: 155416.

[19]Hohenberg P, Kohn W.Inhomogeneous electron gas[J].Phys Rev B, 1964, 136: 864-871.

[20]Kohn W, Sham L J.Self-consistent equations including exchange and correlation effects[J].Phys Rev A, 1965, 140: 1133-1138.

[21]Blöchl P E.Projector augmented-wave method[J].Phys Rev B,1994, 50: 17953-17979.

[22]Perdew J, Wang Y.Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation[J].Phys Rev B, 1986, 33: 8800-8802.

[23]Perdew J P, Chevary J A, Vosko S H, et al.Atoms, molecules,solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation[J].Phys Rev B,1992, 46: 6671-6687.

[24]Perdew J, Wang Y.Accurate and simple analytic representation of the electron-gas correlation energy[J].Phys Rev B, 1992, 45:13244-13249.