由磁矩计算磁场强度

张新邦,陈德祥,王东盛

(北京控制工程研究所,北京100190)

0 引言

磁学中磁矩的模型有偶极子模型和电流环模型[1]，各模型有自已经典的计算周围磁场强度的方法，但计算复杂，不易使用和推广，所以推导一个统一简单有效的由磁矩计算磁场强度的解析表达式是有意义的。

通过对磁矩的2种模型进行推导可得到简单的磁场强度计算公式，这有利于对磁矩周围磁场强度的分析理解和计算。同时如果已知磁矩位置、测点位置和测点的磁场强度，根据表达式可以反推出磁矩的值。

1 由磁矩计算磁场强度公式

物体磁性能的大小可用磁矩来描述，由磁矩可计算出空间某点Q的磁场强度，当物体(磁矩载体)的尺寸相对到点Q的距离是小量，则Q点的磁场强度可以用简单的公式来表达。

图1 由磁矩求磁场强度示意图Fig.1 Schematic diagram of calculatingmagnetic field intensity bymagnetic moment

设磁矩m位于坐标系原点O，方向与x轴相同。点Q在xy平面内，用R代表矢量m与R之间的夹角为θ。在Q点由m贡献的磁场强度为H，H的径向分量为Hr，切向分量为Ht，如图1所示。R与m分别为R与m的模。

当磁矩的物理尺寸相对于R是一个小量时，即如果由通电螺旋线圈或磁棒产生的磁矩，要求螺旋线圈或磁棒的长度相对于R是小量；如果由电流环产生的磁矩，电流环的直径相对于R是小量，则有：

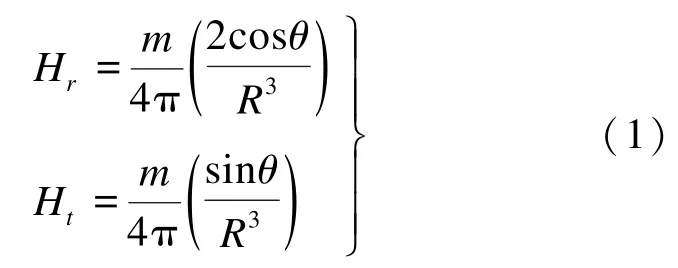
式中：Hr和Ht是磁场强度H的径向和切向分量，A·m-1；m为磁矩，A·m2；R为距离，m。 当介质为空气时，Q点的磁感应强度为

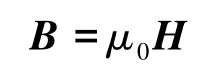
式中：μ0为真空磁导率，μ0=4π ×10-7H/m；B 为磁感应强度，T。如取B的单位为nT，则有

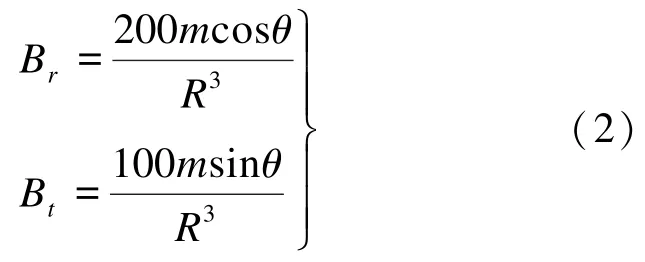
当θ=0时有

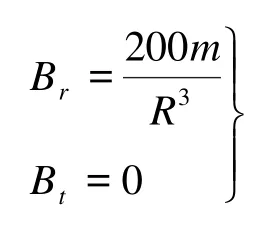
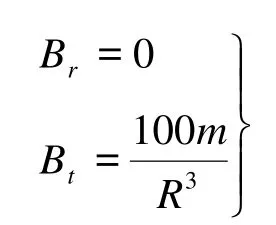
上面公式说明磁场强度反比于距离的立方，所以可简称为反立方公式。

2 公式推导

2.1 由偶极子组成磁矩

偶极子中心位于坐标原点O，磁极强度为p，极间距离AB为l，如图2所示，则磁矩m=pl，方向与x轴相同。在xy平面内有Q点，坐标为(x，y，0)，若Q点不在xy平面内，则适当转动x轴即可。

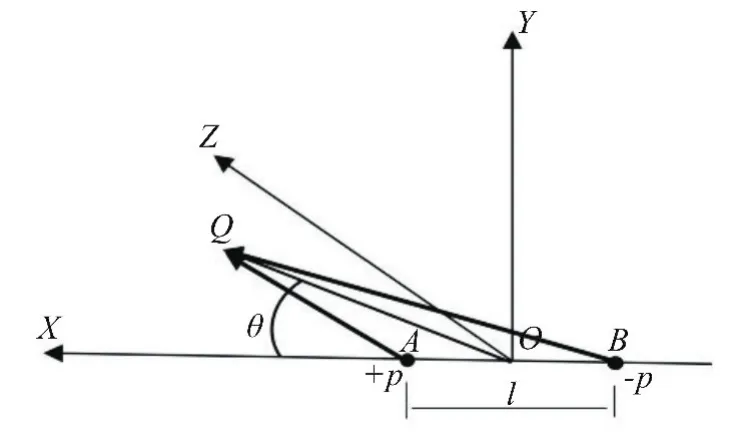
图2 由偶极子组成磁矩Fig.2 Magnetic moment com posed by dipole

根据由磁极计算磁场的公式，Q点的磁场强度H为

设R=OQ，R与x轴的夹角为θ，根据三角公式有

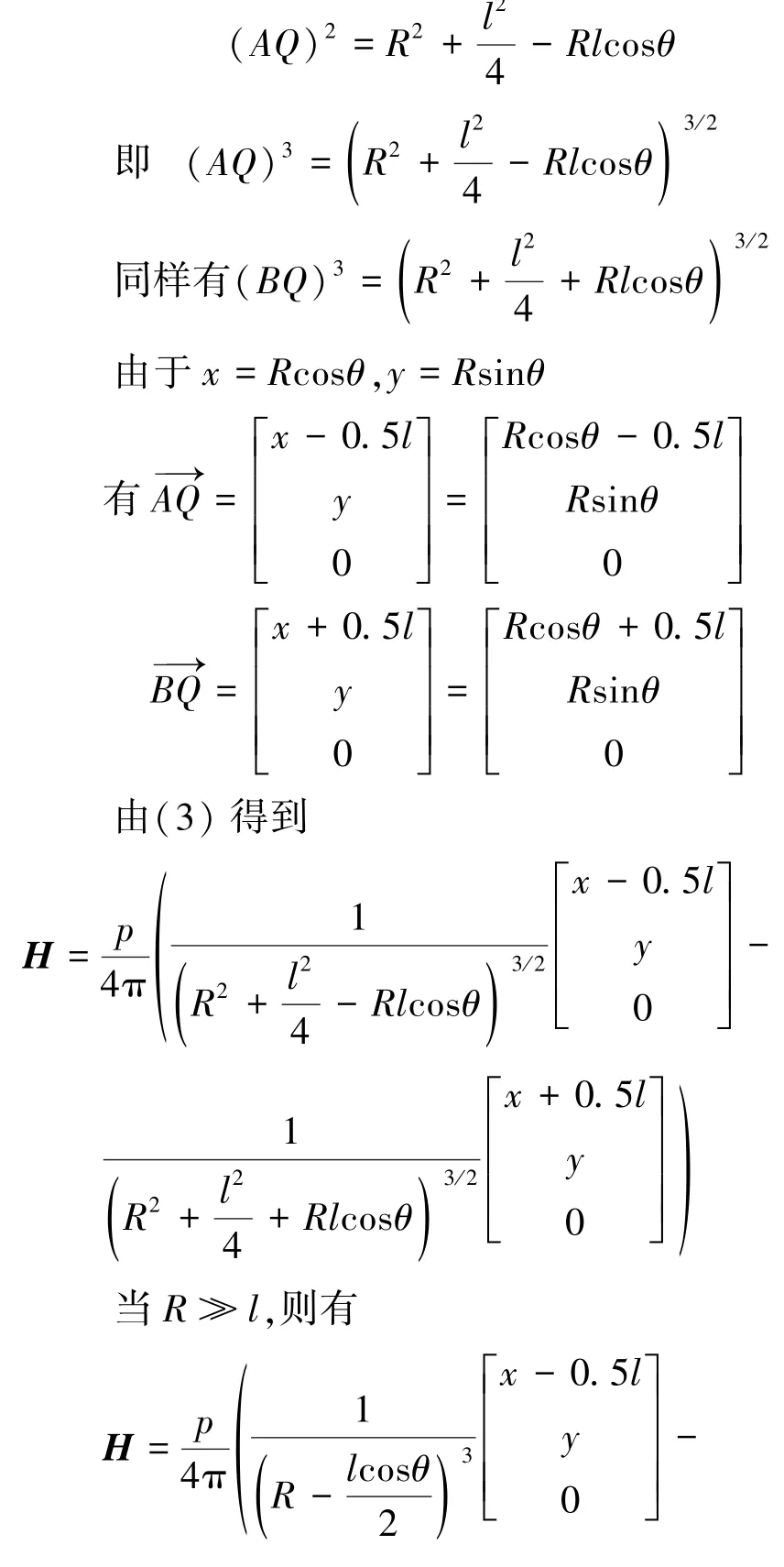
设图2所示的坐标系是r坐标系，将r坐标系绕z轴(即绕O点顺时针)转角度θ，得到新的s坐标系，转换矩阵为A，有

在s坐标系内，Q点磁场强度表示为H(s)，有

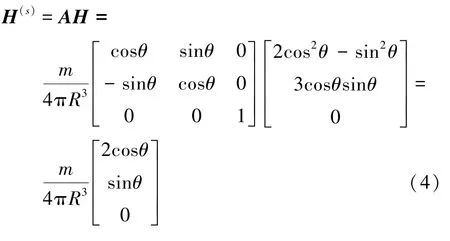
s坐标系内x轴用xs表示，y轴用ys表示，有xs与Hr同方向，ys与Ht同方向。所以式(4)和式(1)是相同的。

2.2 由电流环组成磁矩

在坐标系O-XYZ内，有正方形电流环ABCD在yz平面内。(由于磁矩正比于电流环面积，与环的形状无关，为计算方便，设电流环为正方形。)电流环中心在坐标系原点O(见图3)，电流环的电流强度为i，电流环边长l，则磁矩m=il2，磁矩方向与x轴相同。Q点在xy平面内，坐标为(x，y，0)。

若Q点不在xy平面内，则适当转动x轴后即可。E、F、G、H分别为正方形四个边长的中心。

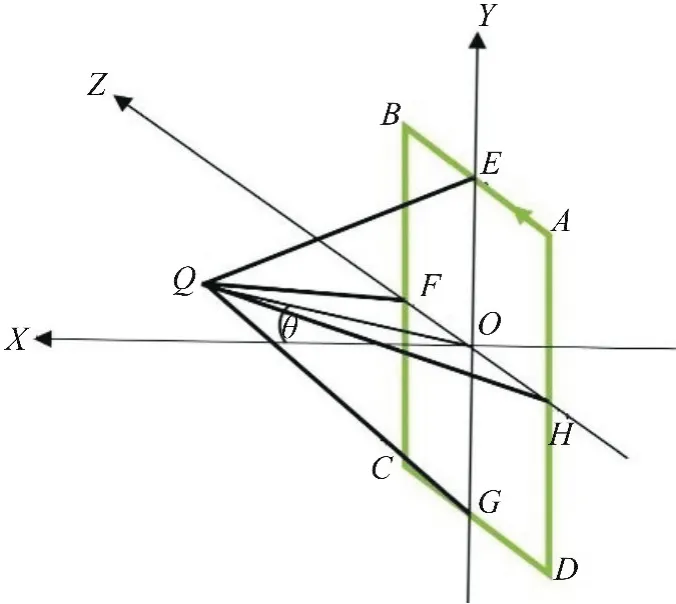
图3 由电流环组成磁矩Fig.3 Magnetic moment com posed by current loop

先分析导线AB在Q点产生的场强HAB。

在导线AB上取一导线元dl，其矢量为dl，设此导线元到Q点的矢量为r，模为r，设矢量RE与r的夹角为α，根据毕奥-萨伐尔定律在Q点由dl贡献的磁场强度dHAB为

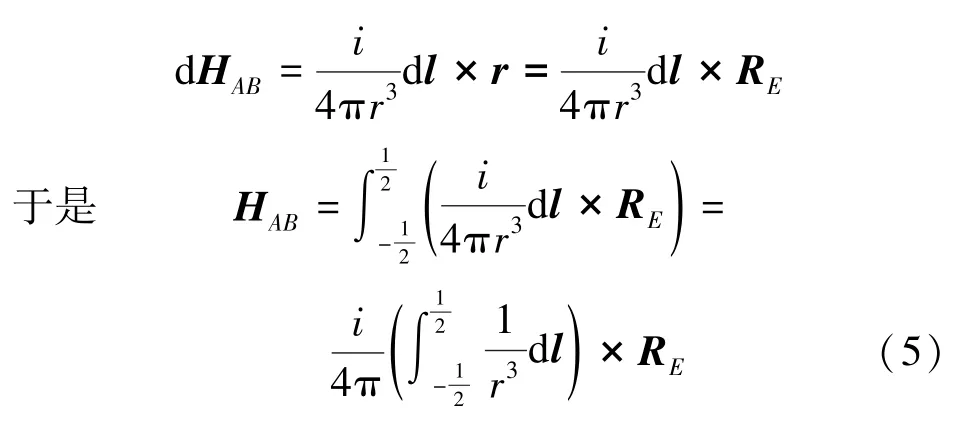
为讨论方便，将图3内导线AB和Q点等单独显示如图4所示，有，于是有

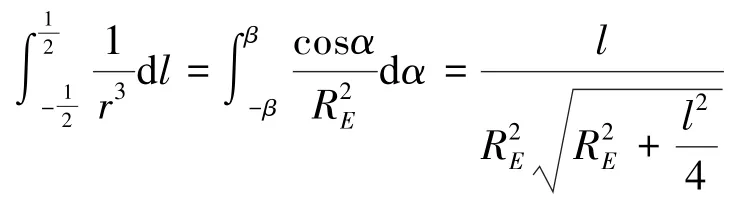
式中β是RE与直线BQ的夹角。

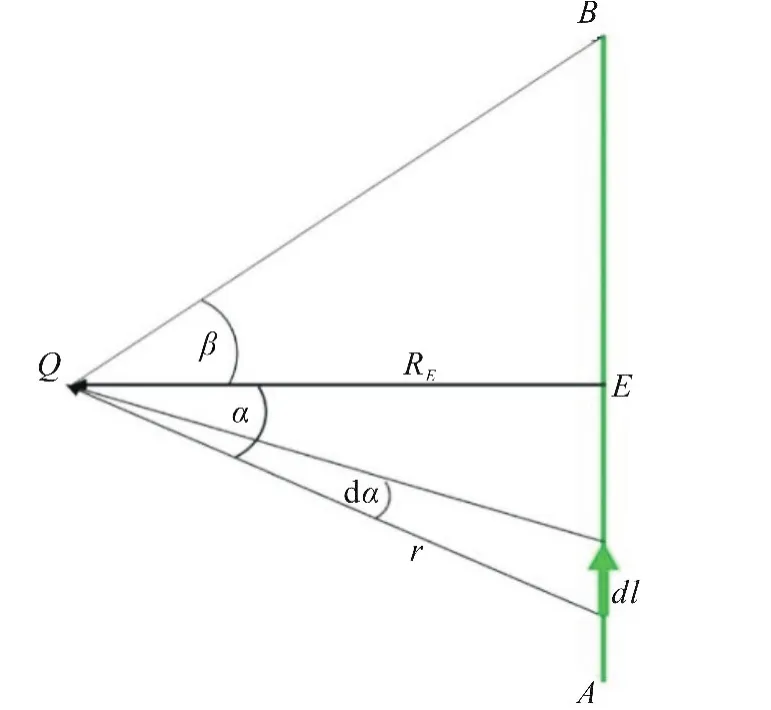
图4 载流导线AB产生的磁场Fig.4 Magnetic field generated by current carrying Wire AB

根据式(5)可以得到下面方程，并为方便对电流环其他边的讨论，方程写成如下形式：

于是Q点的磁场强度H为

H=HAB+HBC+HCD+HDA

设H的3个分量为Hx、Hy、Hz，于是

设图3所示是r坐标系，将r坐标系绕z轴转θ角，得到新的s坐标系，转换矩阵为A，在s坐标系内Q点的磁场强度值表示为H(s)，则有

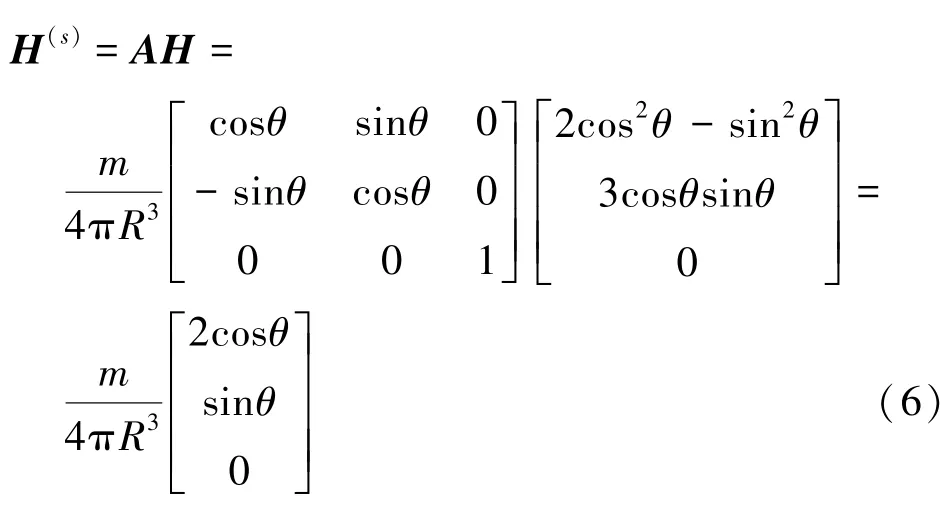
s坐标系内的x轴用xs表示，y轴用ys表示，有xs与Hr同方向，ys与Ht同方向。所以公式(6)和公式(1)的内容是一样的。

应当指出，上面的推导方法不佳，十分繁杂。许多教科书内有相似内容[2-3]，其推导过程简洁而优美，但需要有场论知识。但教科书内推导结果的表达方式不佳，其推导的目的只是证明在远距离情况下，偶极子和电流环的贡献完全一样。本文将2个结果综合，提出了由磁矩计算磁场的表达式，这是由物体的与磁有关物理量直接计算磁场的第3个公式，前2个分别是毕奥-萨伐尔定律和磁极公式。

3 公式应用分析

前面提到应用公式的条件是物体(磁矩载体)的尺寸相对于到测点的距离是小量，下面对此作进一步分析。

3.1 公式应用条件

下面分析这小量的具体概念。

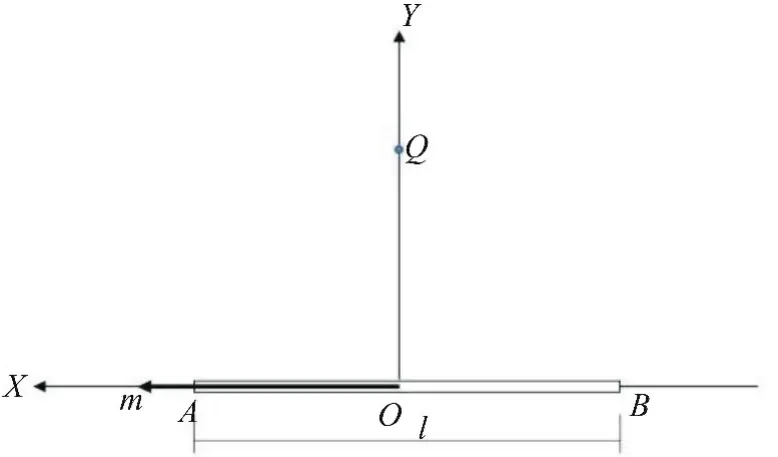
图5 公式应用的条件分析Fig.5 Conditional analysis of formula application

以图5为例，有通电螺旋线圈AB的中心位于坐标原点，线圈的磁矩为m，线圈长度为l，有Q点位于y轴，坐标为(0，y，0)。

当m=20 A·m2，l=1 m，y取不同数值，分别应用反立方公式和偶极子公式得到Q点的磁感应强度数据，由于数据的y、z分量都为0，所以只选用x轴分量，见表1。

由表1看出：当距离是磁棒长度2倍时误差在10%以内，3倍时误差在5%以内，6倍时误差约为1%，所以可按照实际情况，当距离是磁棒长度的3～6倍时可以应用反立方公式。

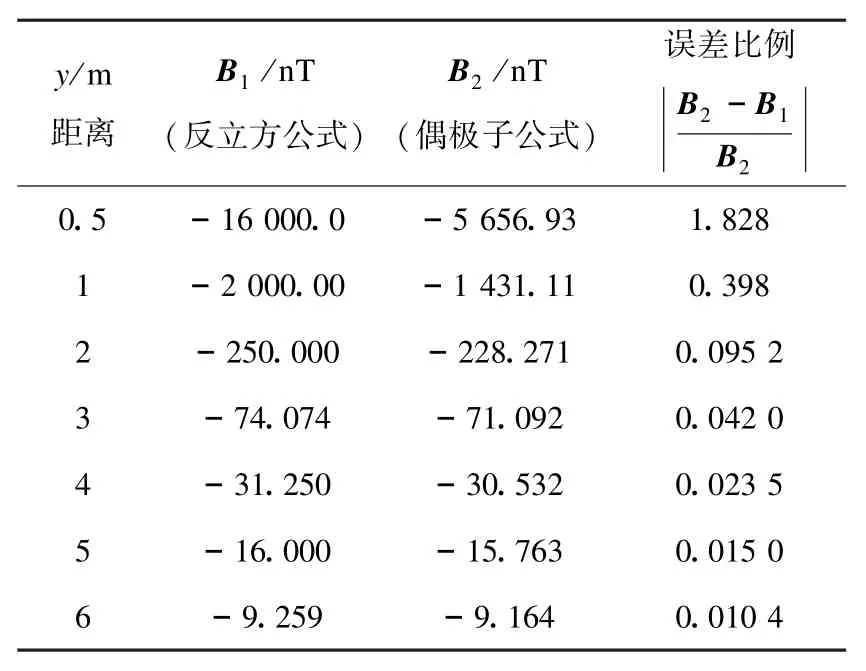
表1 反立方公式和偶极子公式数据比较Table 1 Data com parison of inverse cubic formula and dipole formula

3.2 近距离时如何应用公式

设物体是均匀磁化，物体磁矩为m，体积为V，单位体积的磁矩为M，(M又称为磁化强度，M=m/V)，将物体划分成众多的小单元，每个单元的体积d V，每个单元的磁矩为d m=M d V。由于每个单元的尺寸比较小，相比于测点的距离是小量，可以应用反立方公式，将所有单元的计算结果求和即得到需要的结果。这种将物体划分成众多小单元磁矩的方法称为磁矩陈列模型法。

以上面的图5为例，当y=0.5 m时，由于距离太近不合适使用反立方公式。参考磁矩阵列模型法，将螺旋线圈沿长度方向分成多个(如100个)等长的小单元，则每单元的长度d l=0.01 m，每单元的磁矩d m=0.2 A·m2，对于每一单元可以应用反立方公式，再将结果相加可以得到Q点的磁场强度。计算结果发现和应用偶极子模型的计算结果几乎完全一样(误差小于0.001%)。所以正确应用磁矩陈列法，结果是足够精确的。

3.3 公式应用分析

文献[4-5]论述了舰船磁场的特性、磁场测量、磁场推算等内容。文献[6-8]重点对潜艇磁场数学模型和磁场测量方法进行论述。以上的论述分析中都没有用到磁矩作为研究工具。本文提出了由磁矩计算磁场强度的反立方公式，以及近距离应用所需要的磁矩阵列法，这样就产生了新的基于磁矩的舰船磁场计算分析方法，对海洋中舰船磁场的研究有重要的意义。

4 结束语

1)传统的应用偶极子和电流环模型计算磁场强度的方法不便于实际应用，提出应用磁矩计算磁场强度的反立方公式，有利于磁场的分析和计算。

2)以反立方公式为基础，提出磁矩阵列模型法，满足了近距离计算的要求。

3)公式说明磁场强度与距离的立方成反比，随着距离的增加，场强快速衰减，物体磁性的细微特征很快消失，即使如长度l远远大于宽度d这样的粗大特征，在距离大于3l～6l时可以忽略，仅剩下磁矩是主角。这对于估计计算舰船潜艇等周围的场强分布是有意义的。