基于Copula函数风险控制的贷款组合优化模型

刘艳萍，付 莹

（大连理工大学管理与经济学部，辽宁大连 116024）

0 引言

贷款组合优化已成为商业银行信贷风险管理的核心之一。现有的贷款组合优化研究，按照风险控制的角度不同，大体可以分为以下三大类：（1）基于均值-方差的组合优化模型；（2）基于VaR风险控制的组合优化模型；（3）基于下偏矩风险控制的组合优化模型。

贷款组合优化模型的现有研究已取得了长足进展，但仍有两个问题有待深入研究：一是没有考虑贷款间的违约相关性，违约相关性对组合损失分布偏锋厚尾产生重要影响，且当极端事件发生时，贷款间的违约相关性决定着银行是否会面临灾难性损失；二是现有研究在风险衡量时往往具有严格的前提假设，大多假设贷款收益率联合分布服从正态分布，而金融数据往往具有尖峰厚尾的分布特征，因此存在由于低估极端事件发生概率而使得风险被低估的问题。

综合考虑以上因素，本研究运用Copula函数拟合贷款收益率的联合分布，进而度量贷款间的违约相关性，以贷款间的违约相关性约束贷款比重，加以VaR约束，建立基于Copula函数风险控制的贷款组合优化模型，控制极端事件发生时由高违约相关性引起的相关违约风险。

1 基于Copula函数风险控制的贷款组合优化原理

1.1 基于Copula函数的违约相关性度量原理

贷款的违约相关性是指贷款之间违约的相互关系，即一笔贷款违约引起另一笔贷款违约的可能性。当贷款间存在高违约相关性时，极端事件的发生便会带来同时违约的风险，而这种风险往往是决策者最为关注的。现有研究度量违约相关性的方法大体分为两种：一是以线性相关系数替代资产间违约相关性，这种方法存在低估极端事件发生概率而低估风险的问题；二是以联合违约概率推导资产间的违约相关性，该方法存在由于违约样本数据稀少而导致测算模型精度下降的问题。

基于Copula函数的违约相关性度量原理。一是运用非参数估计法求解三类Copula函数解析式，二是通过K-S检验选择最优Copula函数，三是运用Copula函数度量贷款间的下尾相关系数，以下尾相关系数反映违约相关性。

本文运用Copula函数度量贷款间的违约相关性，原因有二：(1)Copula函数对贷款组合收益率的边际分布没有限制，可根据贷款组合的实际情况进行拟合，能够更加准确的反应贷款间的非线性相关关系；(2)运用Copula函数度量的下尾相关系数反映贷款间的违约相关性，弥补采用线性相关系数不能准确反映贷款间违约相关性的问题，避免采用联合违约概率度量违约相关性时由于违约数据稀少影响模型精度的问题。

1.2 基于Copula函数的贷款组合风险控制原理

以最优Copula函数度量的下尾相关系数反映贷款间的违约相关性，通过违约相关性约束贷款的分配比重，将高违约相关性的贷款控制在一定比例以下，从而控制贷款组合的风险。

设xi,xj分别为第i类企业和第j类企业的贷款分配比重，rijlo为第i类企业与第j类企业的下尾相关系数即违约相关性，则风险控制原理可表示为：

其中，A为取值范围在(0,1)的常数，用以约束第i类和第j类企业贷款的分配比重，银行可根据自身的风险偏好设定A的值。如果设A=0.2，式(1)可表示为(xi+xj)rijlo≤0.2，当rijlo=1时，xi+xj≤0.2，当rijlo=0.8时，xi+xj≤0.25，经济学意义为当两类贷款违约相关性为1时，两类贷款的分配比重之和要低于20%，当两类贷款违约相关性为0.8时，两类贷款的分配比重之和要低于25%。式(1)考虑了贷款间的违约相关性，通过违约相关性约束各类贷款分配比重，具有高违约相关性低贷款比重的特性，最终实现贷款组合风险控制的目的。

1.3 基于VaR的风险控制原理

VaR是指在一定概率水平下，贷款组合在未来特定的一段时间内的最大可能损失。可表示为：

其中，DP为贷款组合在持有期内的损失，c为置信度即给定的概率水平，可由银行根据需要自行取值。

基于VaR的风险控制原理是在一定置信度下将贷款组合的损失控制在银行可接受的范围内，可用于控制贷款的整体风险。本文运用收益率的波动来反映组合的整体风险，所以VaR约束以收益率的形式表现。

1.4 基于Copula函数风险控制的贷款组合优化原理

(1)利用非参数估计法求解三类Copula函数的解析式，对贷款收益率进行概率积分变换，通过K-S检验选择对贷款相关结构拟合最好的Copula函数。

(2)运用最优Copula函数度量贷款组合的下尾相关系数，以下尾相关系数反映贷款间的违约相关性，通过违约相关性约束贷款的分配比重，从而控制由极端事件发生而引起的相关违约风险。

基于Copula函数风险控制的贷款组合优化原理就是运用Copula函数度量贷款间的违约相关性，根据贷款间的违约相关性约束贷款的分配比重，再加以VaR约束，以贷款组合收益率最大化为目标函数，确定贷款分配比重。

2 基于Copula函数风险控制的贷款组合优化模型

2.1 Copula函数的参数估计

2.1.1 模型的基本参数

银行的法定存款准备金等无风险资产具有固定收益的性质，可看作是银行的无风险贷款，表1给出银行无风险资产的种类及利率。

表1 商业银行资产利率一览表

由于无风险资产不存在违约问题，因此在度量贷款的违约相关性时仅考虑n类企业贷款，这n类企业贷款的各年收益率见表2。

本文运用二元Copula函数度量各类贷款间的违约相关性，设ri—第i类贷款的收益率随机变量，F(ri)—第i类贷款收益率的边缘分布函数；rj—第j类贷款的收益率随机变量，F(rj)—第j类贷款收益率的边缘分布函数，则Copula函数可对两类贷款的联合分布C(F(ri),F(rj))进行拟合。

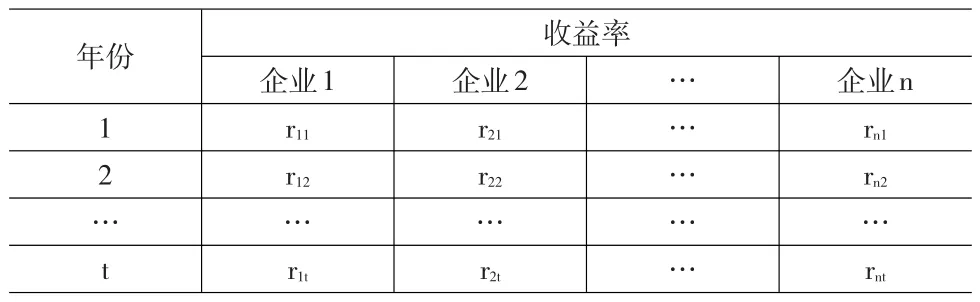
表2 m 银行对n类企业贷款的t年的收益率rik

Copula函数的参数估计可以分为参数估计方法和非参数估计方法，参数估计方法(如：极大似然估计)是先假定其边缘分布函数，再进行相应的参数估计，但边缘分布函数设定的错误会直接导致Copula函数估计产生偏差。非参数估计方法不需要事先知道变量的边缘分布函数，因此本文选择基于Kendall秩相关系数t的非参数估计法求解Copula函数解析式。

设(ri1,ri2)、(rj1,rj2)是贷款收益率随机变量 ri、rj的两个观测值，则(ri1-ri2)和(rj1-rj2)分别表示随机变量ri、rj的变化。若(ri1-ri2)(rj1-rj2)＞0，则称它们变化一致；若(ri1-ri2)(rj1-rj2)＜0，则称它们变化不一致，可得贷款收益率ri和rj的Kendall秩相关系数t的表达式[13]：

其中，c表示一致的观测值的数量，d表示不一致的观测值的数量，可见t是用来度量变量间变化的一致性程度，其取值范围在[-1,1]之间，若ri与rj的变化完全一致，t=1；若ri与rj的变化完全不一致，t=-1。

2.1.2 三类Copula函数

在选取Copula函数时考虑三个因素：单一参数；具有尾部相关性测度；在金融建模中较为常用。综合考虑以上因素确定本文的备选Copula函数为：Gumbel、Clayton和A12。

这三类Copula函数的参数θ与Kendall秩相关系数t有着对应关系式，即可通过t的值估计参数θ的值。

(1)Gumbel Copula函数

其分布函数的表达式为：

其中：

(2)Clayton Copula函数

其分布函数的表达式为：

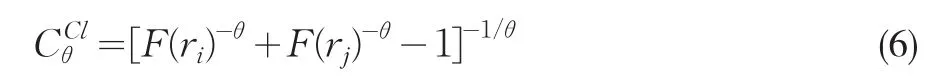
其中：

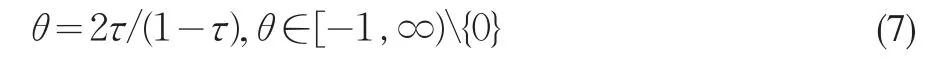
(3)A12 Copula函数

其分布函数的表达式为：

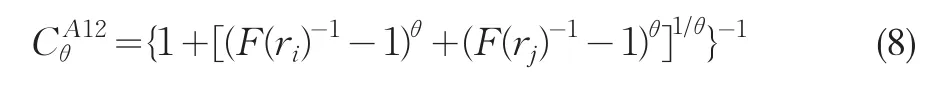
其中：

本研究通过非参数估计求解上述三类Copula函数解析式，对贷款收益率联合分布进行拟合，选择拟合优度最好的Copula函数，用其度量贷款间的违约相关性。

2.2 最优Copula函数的选择

本研究通过K-S检验对Copula函数的拟合优度进行评价，选择出最优Copula函数。K-S检验是一种非参数检验方法，优点在于对小样本数据依然适用，解决了样本数据不符合检验方法中大样本假设的问题。K-S检验用于计量经验分布函数与理论分布函数之间的偏差，其统计量为：

由式(10)可知，D值越小，则证明经验分布函数与理论分布函数的偏差越小，即拟合优度越好；反之，D值越大拟合优度越差。也可通过判断检验统计量的概率p值是否大于显著性水平检验拟合效果，一般若p＞0.05则认为通过拟合优度检验。本研究综合考虑统计量D值和概率p值，依据理论Copula分布函数与贷款累计经验分布函数偏差最小原则选取最优Copula函数。

K-S检验只适用于一元分布，如对变量的边缘分布检验，而本研究将其运用于最优Copula函数的选择，是用于评价Copula函数对两类贷款联合分布的拟合情况，属于二元分布，因此需要将二元分布转化为一元分布形式。本文通过阿基米德Copula的生成元将二元Copula转为单变量分布函数KC(t)，KC(t)定义为：φ(t)为阿基米德Copula函数的生成元，具体表达式为：

(1)Gumbel Copula函数

(2)Clayton Copula函数

(3)A12 Copula函数

本研究运用K-S检验选择最优Copula函数，具体按照以下步骤：

①对贷款收益率进行概率积分变换，变换后的贷款收益率累积分布函数服从(0,1)均匀分布；

②将变换后的数据分别代入公式(4)、公式(6)和公式(8)，求出tGu=CqGu(F(ri),F(rj))、tCl=CqCl(F(ri),F(rj))和tA12=CqA12(F(ri),F(rj))；

③将步骤②求出的 t代入公式(11)～(14)，得到 KCGu(t)、KCCl(t)和 KCA12(t)；

④对步骤③得到的KCGu(t)、KCCl(t)和KCA12(t)进行K-S检验。

2.3 贷款的违约相关性

由K-S检验可选出最优Copula函数，用最优Copula函数度量贷款间的下尾相关系数。下尾相关系数是指某一资产大幅下跌对其他资产的影响程度，可以较好地反映贷款间的违约相关性。ri和rj两类贷款的下尾相关系数可以表示为：

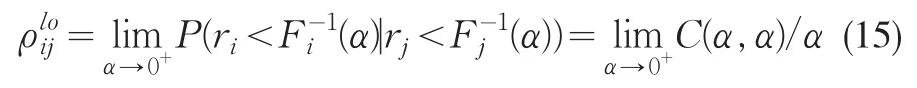
其中，a表示概率值，Fi-1(a)、Fj-1(a)表示对应于a的分位数。将选出的最优Copula函数代入式(15)中的C(a,a)便可求得下尾相关系数rijlo，即两类贷款的违约相关性。

2.4 优化模型的建立

2.4.1 目标函数的建立

表2中给出n类企业t年的贷款收益率，则第i类企业贷款的期望收益率为：

优化模型的目标函数为：

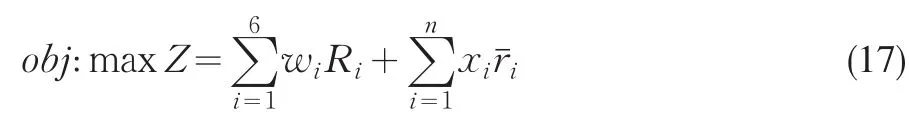
wi—为第i类无风险资产的分配比重，Ri—为第i类无风险资产的收益率，见表1；xi—为第i类企业贷款的分配比重为第i类企业贷款的期望收益率，见表2和式(16)。目标函数的第一个和式代表无风险资产的组合收益率，第二个和式代表企业贷款的组合收益率，因此，式(17)代表银行资产收益最大化。

2.4.2 约束条件的建立

首先引入基于Copula函数的风险控制约束，用以控制由极端事件发生而引起多笔贷款同时违约的风险，由式(1)和式(15)得：

其次引入风险价值VaR约束，用以控制收益的总体风险，设置信水平为95%，则约束条件为：

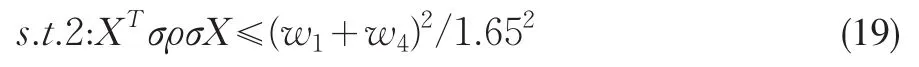
引入法律、法规约束。

存贷比例的限制：

备付金比例的限制：

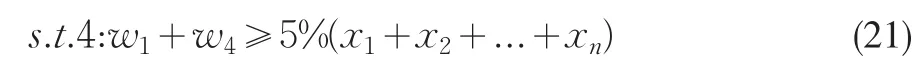
拆出资金比例的限制：

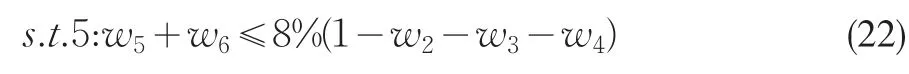
法定存款准备金比例限制：

系统内存款准备比例限制：

引入银行经营监管约束。

基于流动性的库存现金比例：

基于盈利性的库存现金比例：

引入贷款的结构约束。

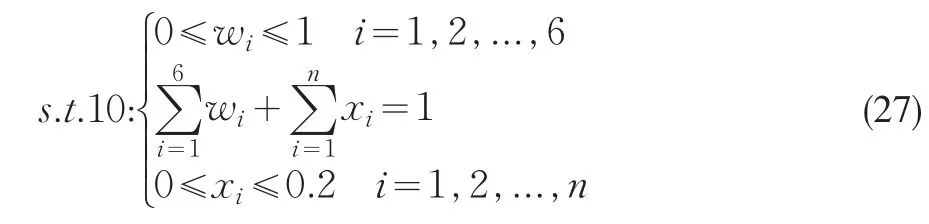
2.5 优化模型的特色

(1)优化模型考虑了贷款间的违约相关性对贷款组合整体风险的影响。提出了基于Copula函数的违约相关性度量原理和基于Copula函数的贷款组合风险控制原理，通过贷款间的违约相关性约束贷款比重，控制由极端事件发生而引起多笔贷款同时违约的高风险。

(2)优化模型运用Copula函数度量贷款组合收益率的联合分布。运用K-S检验选择最优Copula函数，以最优Copula函数拟合贷款收益率联合分布的真实情况。Copula函数对贷款组合收益率的边际分布没有限制，能够准确地刻画贷款组合间的相关结构。

(3)优化模型运用Copula函数度量贷款间的违约相关性。以Copula函数计量的下尾相关系数反映违约相关性，弥补采用线性相关系数不能准确反映贷款间违约相关性的缺憾，解决以联合违约概率度量违约相关性时由于违约数据稀少而影响模型精度的问题。

3 应用实例

3.1 样本数据

银行执行的资产利率实际情况见表1，同时，银行拟对7类企业进行贷款，并内部保留这7类企业15年的贷款实际收益率数据，如表3所示。

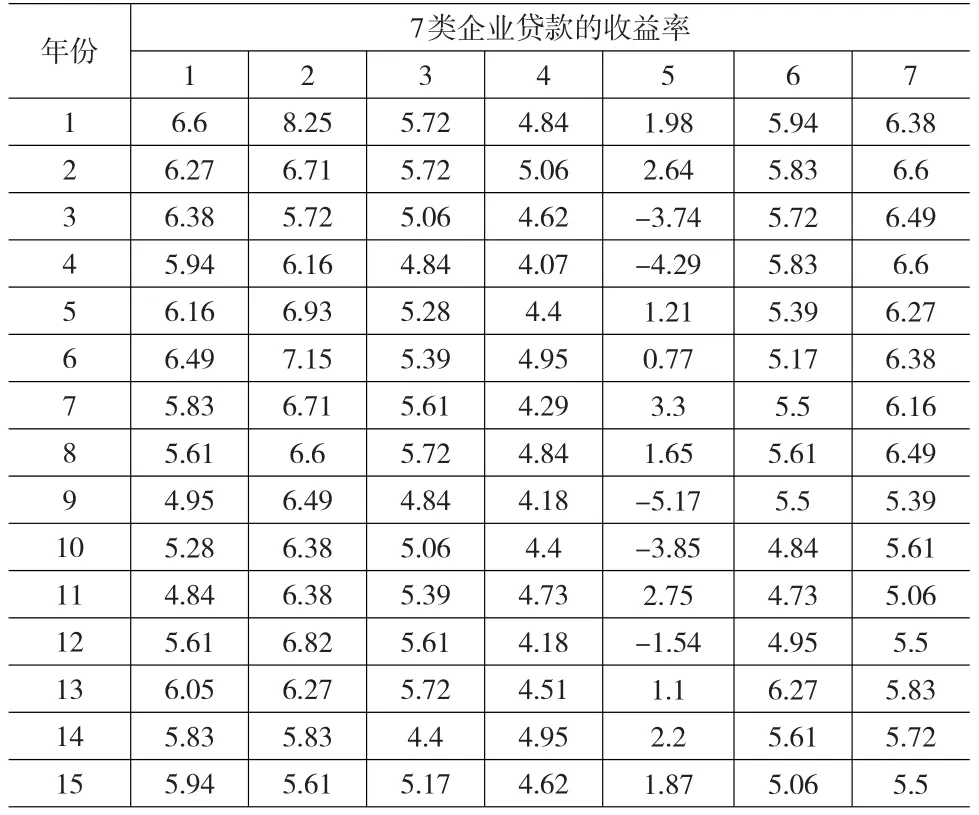
表3 银行年贷款收益率rik一览表(%)

3.2 贷款组合间违约相关性的计算

3.2.1 贷款秩相关系数t的计算

将表3中的任意两类贷款的收益率序列代入到公式(3)中，可得到两类贷款的秩相关系数t，如表4所示。

表4 各企业贷款收益率的秩相关系数

3.2.2 贷款组合联合分布函数的确定

以企业1与企业2两类贷款为例，对三类Copula函数进行参数估计，求两类贷款的联合分布函数。

(1)Gumbel Copula函数

由表4可知企业1与企业2的秩相关系数t=0.215，将t值代入到式(5)中，可得Gumbel Copula函数的参数θ估计值：

θ=1-t=1-0.215=0.785

将θ=0.785代入到式(4)中，可得基于Gumbel Copula的企业1与企业2的联合分布函数：

(2)Clayton Copula函数

将t=0.215代入到式(7)中，可得Clayton Copula函数的参数θ估计值：

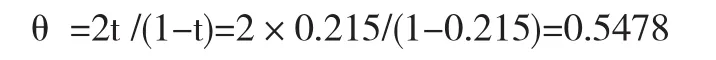
将θ=0.5478代入到式(6)中，可得基于Clayton Copula的企业1与企业2的联合分布函数：

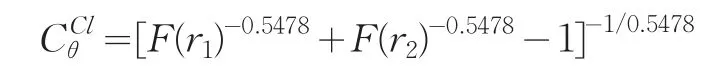
(3)A12 Copula函数

将t=0.215代入到式(9)中，可得A12 Copula函数的参数θ估计值：

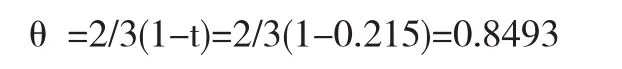
将θ=0.8493代入到式(8)中，可得基于A12 Copula的企业1与企业2的联合分布函数：

由企业1和企业2两类贷款的参数估计及联合分布函数计算过程，同理可得7类企业贷款中任意两类贷款的参数估计和联合分布函数，三类Copula函数的参数θ估计值如表5所示。

若想求得7类企业贷款中任意两类贷款的联合分布函数，需对三类Copula函数分别进行21次(C72)参数估计，由于A12 Copula的参数θ高达15次不在定义域[1,∞)内，所以不具有分析意义，在最优Copula选择时重点分析Gumbel Copula和Clayton Copula。

表5 三类Copula函数的参数估计值

3.2.3 最优Copula函数的选择

本研究运用K-S检验的方法选择最优Copula函数，仍以企业1和企业2为例，具体步骤如下：

(1)对企业1和企业2的贷款收益率进行概率积分变换，将变换后的收益率代入公式(4)和公式(6)，式中的θ值分别为0.785和0.5478，求得：

tGu=(0.011193559 0.008972525 0.007936487 0.007956393 0.009083972 0.009761944 0.008424635 0.008033682 0.007102007 0.007403987 0.006863645 0.008261786 0.008207384 0.007466773 0.007340148)-1

tCl=(0.026184381 0.022710764 0.020955603 0.021003798 0.022881357 0.023992139 0.021775142 0.021102889 0.019422845 0.020001356 0.018994929 0.021475118 0.021432647 0.020156659 0.019930204)-1

(2)求两类Copula的单变量分布序列KC(t)。对于Gumbel Copula，由式(11)和式(12)可得：

将θ值和步骤(1)中求得的t值代入式(28)，可得：

KCGu(t) =(0.075252324 0.062848688 0.056832168 0.056949325 0.063486479 0.067329602 0.059687146 0.057403597 0.051861638 0.053674066 0.050419517 0.058738822 0.058421112 0.054048903 0.053292246)-1

对于Clayton Copula，由式(11)和式(13)可得：

将θ值和步骤(1)中求得的t值代入式(29)，可得：

KCCl(t) =(0.067486382 0.058956453 0.0546075 0.054727279 0.059377725 0.062114721 0.056641507 0.054973484 0.050787251 0.052231631 0.049716882 0.055897565 0.055792191 0.05261886 0.052054149)-1

(3)对KCGu(t)和KCCl(t)分别作K-S检验，求得统计量D值和概率p值，结果如表6所示。

表6 K-S检验结果(企业1与企业2)

由表6可得，Clayton Copula的D值小于Gumbel Copula的D值，因此Clayton Copula的拟合优度更好，并且Gumbel Copula的p值小于0.05，说明Gumbel Copula不能通过K-S拟合优度检验，综上考虑，应选择Clayton Copula拟合企业1和企业2的贷款收益率联合分布函数。

同理，对7家企业中任意两家企业的联合分布函数进行拟合优度K-S检验，检验结果如表7所示。

表7 K-S检验结果

为衡量两类Copula函数的整体拟合优度情况，对21次K-S检验结果的D值求均值。

(4)贷款组合间违约相关性的计算

将式(6)代入到式(15)中，可得基于Clayton Copula的下尾相关系数表达式：

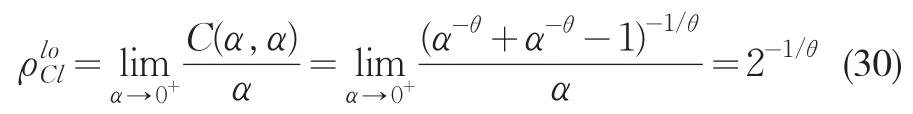
将表5中Clayton Copula的θ值代入式(30)，可得贷款组合间的违约相关性矩阵，如表8所示。

表8 贷款组合间的违约相关性

3.3 优化模型的求解

3.3.1 目标函数的建立

将表3中数据代入式(16)，可得企业贷款的期望收益率，将7类企业贷款期望收益率和表1中的6类无风险资产利率代入公式(17)，得优化模型目标函数：

obj:maxZ=0×w1+0.0252×w2+0.0252×w3+0.0252×w4+0.03×w5+0.033×w6+0.05852×x1+0.06534×x2+0.05302×x3+0.04576×x4+0.00058667×x5+0.05463333×x6+0.05998667×x7

3.3.2 基于Copula函数风险控制约束的建立

式(18)是基于Copula函数风险控制约束的具体表达式，其中A为商业银行根据自身风险偏好设定的值，本研究将其设为0.2，则基于Copula函数的风险控制约束如式(31)所示：

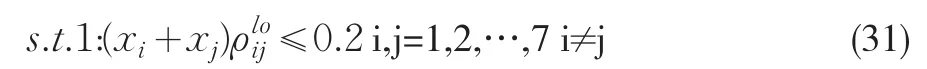
3.3.3 风险价值VaR约束的建立

VaR约束是用于控制贷款组合的整体风险，将贷款收益率标准差矩阵s和相关系数矩阵r代入到式(19)中，可得VaR约束条件：

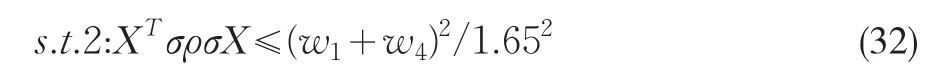
3.3.4 法律、法规和银行经营管理约束的建立

法律、法规约束的建立。

由式(20)得存贷比例约束：

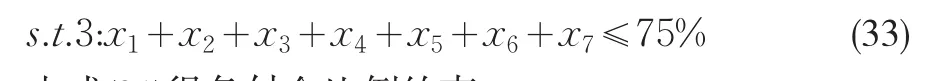
由式(21)得备付金比例约束：

由式(22)得拆出资金比例约束：

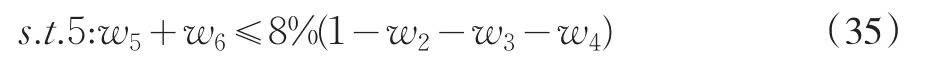
由式(23)得法定存款准备金比例约束：

由式(24)得系统内存款准备比例约束：

引入银行经营监管约束。

由式(25)得流动性的库存现金比例约束：

由式(26)得盈利性的库存现金比例约束：

由式(27)得贷款的结构约束：

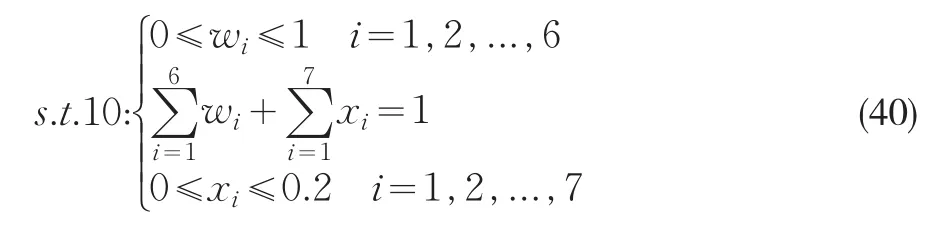
3.3.5 模型求解

为便于下文进行对比分析，将上文模型设定为模型一，基于以上目标函数与约束条件，对模型一进行编程求解，得无风险资产和7类企业贷款分配比例，如表9中第2列所示。

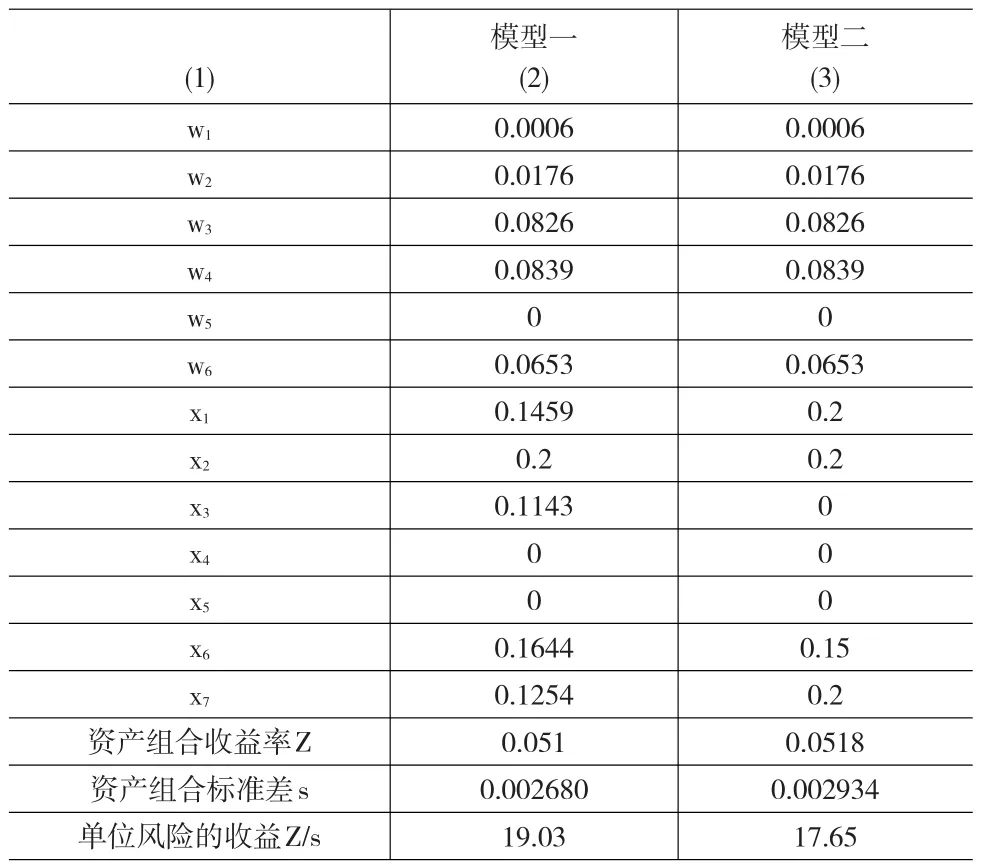
表9 无风险资产与企业贷款分配比例表

3.3.6 对比分析

将模型一中基于Copula函数风险控制约束式(31)去掉可得模型二，表9中第3列列出模型二的无风险资产和7类企业贷款分配比例。

参见表9对比分析两个模型的分配结果可得：

(1)模型一的资产组合收益率为5.1%，模型二为5.18%，模型一略低于模型二。模型一的资产组合标准差为0.268%，模型二为0.2934%，模型一低于模型二。模型一的收益率虽然略低于模型二，但控制风险的能力明显强于模型二。

(2)模型一单位风险的收益为19.03，模型二为17.65，模型一高于模型二。

通过上述比较分析可得，基于Copula函数风险控制的贷款组合优化模型(模型一)，组合具有较小的风险和较高的单位风险收益，证明模型一能够较好地控制组合的整体风险，并提高了银行资产组合的单位风险收益。

4 结论

(1)提出基于Copula函数的违约相关性度量原理和基于Copula函数的贷款组合风险控制原理，建立了基于Copula函数风险控制的贷款组合优化模型，通过贷款间的违约相关性约束贷款比重，避免了由极端事件发生引起贷款同时违约的高风险。

(2)运用Copula函数度量贷款组合收益率的联合分布。通过K-S检验选择最优Copula函数，以最优Copula函数拟合贷款收益率联合分布，准确地刻画了贷款组合间的相关结构，真实反映了贷款组合存在的风险，解决了现有研究假设贷款收益率服从正态分布存在低估风险的问题。

(3)运用Copula函数度量的下尾相关系数反映贷款间的违约相关性。弥补了采用线性相关系数不能准确反映贷款间违约相关性的缺憾，解决了采用联合违约概率度量违约相关性时由于违约数据稀少而影响模型精度的问题。

[1]Markowitz H.Portfolio Selection:Efficient Diversification of Invest⁃ments[J].The Journal of Finance,1952,7(1).

[2]Rasmussen K M,Clausen J.Mortgage Loan Portfolio Optimization Us⁃ing Multi-stage Stochastic Programming[J].Journal of Economic Dy⁃namics and Control,2006,30(1).

[3]许文,迟国泰,隋聪.基于全部贷款组合风险度控制的新增资产组合优化模型[J].金融管理,2009,21(6).

[4]Dietsch M,Petey J.The Credit Risk in SME Loans Protfolios：Model⁃ing Issues,Pricing,and Capital Requirements[J].Journal of Banking and Finance,2002,26(2/3).

[5]迟国泰,奚扬,姜大治,林建华.基于VaR约束的银行资产负债管理优化模型[J].大连理工大学学报,2002,42(6).

[6]刘艳萍,王婷婷,迟国泰.基于风险价值约束的贷款组合效用最大化优化模型[J].系统管理学报,2009,18(2).

[7]武敏婷，孙滢，高岳林.基于VaR约束的均值-绝对偏差投资组合优化模型及实证研究[J].统计与决策,2010,(3).

[8]Prakash A J,Chang C H,Pactwa T E.Selecting a Portfolio with Skew⁃ness:Recent Evidence from US,European,and Latin American Equi⁃ty Markets[J].Journal of Banking and Finance,2003,（27）.

[9]迟国泰,迟枫,闫达文.贷款组合的“均值—方差—偏度”三因素优化模型[J].运筹与管理,2009,18(4).

[10]潘东静.半方差约束下的模糊随机收益率贷款组合优化模型[J].计算机科学,2010,37(5).

[11]Sklar A.Fonctions de Répartition à n Dimensions et Leurs Marges[J].Publications de l'Institut de Statistique de L'Université de Paris,1959,（8）.

[12]Nelsen R B.An Introduction to Copulas[M].New York:Springer,1998.

[13]Li D X.On Default Correlation:a Copula Function Approach[J].Journal of Fixed Income,2000,9(4).

[14]童中文,何建敏.基于Copula风险中性校准的违约相关性研究[J].中国管理科学，2008,16(5).