基于累积前景理论和随机加权法的随机多准则决策方法

胡军华，杨 柳

（中南大学商学院，长沙 410083）

0 引言

在现实世界中，因为环境的不确定性和复杂性，随机多准则决策问题广泛存在。在随机多准则决策问题中，准则值概率分布有确定、模糊确定和部分完全不确定三种情况。对于概率分布确定的随机多准则决策方法的研究比较多，如随机优势方法、随机多目标可能度方法SMAA等；对于概率模糊确定的随机多准则决策方法的研究近年来也逐渐兴起，如基于区间粗糙算子的粗糙随机多准则决策方法，基于期望值-混合熵的区间概率模糊随机多准则决策方法；而概率部分完全不确定的随机多准则决策方法的研究比较少，该方法对缺失值的处理，通常利用回归分析和基于贝叶斯推理等方法，采用可能值进行填充。随机加权法[1]是在Bootstrap法基础上，通过对观测数据的重新抽样产生再生样本，进而估计分布参数的一种有效方法。随机加权法对概率密度函数未知的随机多准则问题进行处理时，可以有效估计出其分布特征，将概率未知问题转化为概率已知的决策问题，再利用相应的方法进行处理。

然而，目前大多数随机多准则决策问题多建立在期望效用理论和完全理性人假设的基础上。而实际上，由于个体认知的局限和知识的匮乏，使得决策者并非完全理性人。因此，Kahneman和Tversky提出了前景理论（Prospect Theory,PT）[2]和累积前景理论（Cumulative Prospect Theory,CPT）[3]，彻底摒弃了理性人假设，通过模型参数的调整来反映行为主体的风险偏好。近年来，考虑决策者风险偏好的随机多准则决策问题引起了一些学者的关注，如Lahdelma和Salminen[4]将前景理论中的成对线性无差异函数和SMAA结合，提出了一种SMAA-P方法。王坚强和周玲[5]利用前景理论的计量模型，探讨了概率和准则值均为区间灰数的灰色随机多准则决策问题。

在上述研究基础上，本文将随机加权法应用于随机多准则决策中，考虑决策者的主观风险偏好态度，针对准则权重未知、准则值部分缺失的随机多准则决策问题，提出一种基于累积前景理论和随机加权法的信息不完全的多准则决策方法。

1 累积前景理论和随机加权法

1.1 累积前景理论

累积前景理论中，前景值V由价值函数v和决策权重函数π共同决定，表示为：

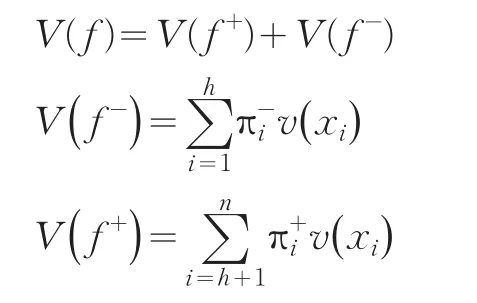
Kahneman和Tversky[3]给出了一种能较好满足决策者面临收益时风险规避和面临损失时风险寻求的偏好特征的价值函数形式，具体表达式如下：

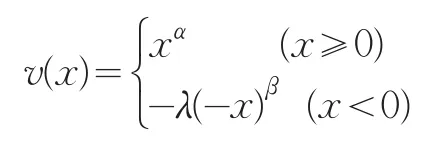
其中，x是决策方案相对于参考点的差值，x为正时，表示收益，x为负时，表示损失，α、β分别为风险偏好和风险厌恶系数。Kahneman和Tversky认为0＜α,β＜1，α=β=1时，决策者可被视为风险中立者。λ为损失规避系数，λ＞1表示决策者对于损失更加敏感。

本文中，收益和损失的决策权重函数采用文献[7]给出的形式，分别为：

Prelec[6]给出了w+和w-的函数形式：

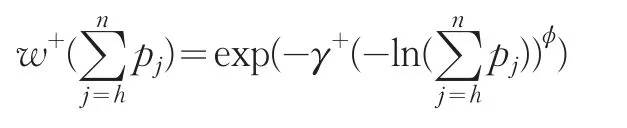
其中，γ+＞0，γ-＞0，ϕ＞0。

1.2 随机加权法

Efron于1979年首次系统提出了Bootstrap方法[7]。该方法不需要对给定的样本数据的分布作任何假设，通过对样本数据抽样来模拟其分布，是一种充分提取样本数据本身信息的非参数统计推断方法。Bootstrap法[8]的基本思想是：已知来自总体分布F的随机子样X=(X1,X2,…,Xn)，R(X,F)为某个事先选定的随机变量，它是X和F的函数。要求根据子样的观测值x=(x1,x2,…,xn)估计R(X,F)的分布特征，如概率密度函数、分布函数、均值或方差等。Bootstrap法就是用样本X=(X1,X2,…,Xn)构造出F的极大似然估计（一般用样本X的经验分布函数Fn来近似）；然后从中抽取大小为n的简单子样i=1,2,…,n，称为Bootstrap子样；最后，用的分布来迫近R(X,F)的分布，称为Bootstrap分布。

1987年，郑忠国在Bootstrap方法的基础上提出的一种新的统计分析法—Bayesian Bootstrap方法，又称随机加权法[1]，其基本思想是：采用蒙特卡洛模拟法从Diricklet分布中重复抽取N组随机变量，通过给每个试验样本随机加权产生再生样本来模拟总体分布，从而获得小样本数据统计分布的均值与方差。设某先验信息服从未知分布F，未知分布的均值为u，方差为σ2。X=(x1,x2,…,xn)为来自于某未知分布F的样本，令未知分布的均值为u和方差为σ2与收集到的样本数据获得的均值Xˉ和方差s2存在一定的误差，记：对于分别构造随机加权统计量：

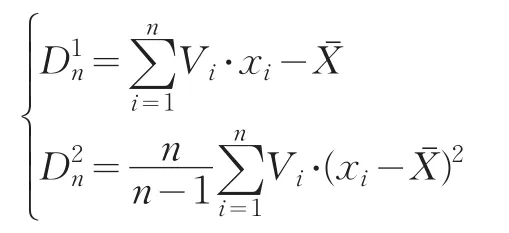
其中Vi(V1,V2,…,Vn)为服从D(1,1,…,1)分布的随机变量。存在如下统计特征：

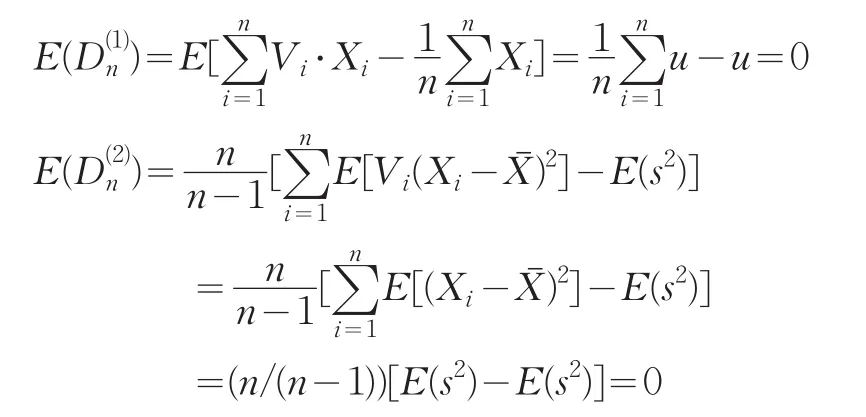
利用Bayesian Bootstrap对子样进行估计的具体步骤如下：

（1）通过计算机随机产生M组服从Dirichlet分布D(1,1,…,1)的随机变量…,M)，记V(j)的联合分布为，按如下方式产生：随机抽取n-1个独立同分布且服从U(0,1)的样本v1,v2,…,vn-1，再按从小到大的顺序重新排序使得=1,2,…,n)，则V(j)的联合分布就是

（2）计算出M组随机加权子样(j=1,2,…,M)。其中:

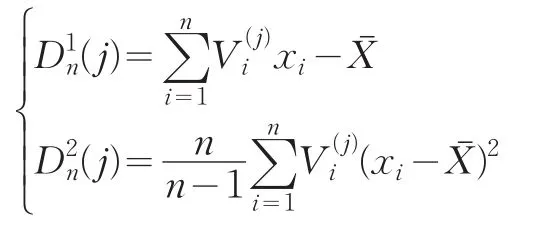
（3）分布参数u,σ2的估计分别为:

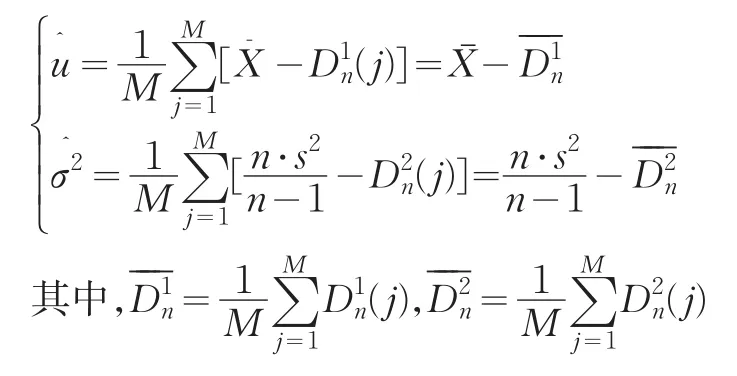
2 随机多准则决策方法

某一随机多准则决策问题，有m个备选方案供选择，记 为A={a1,a2,…,am}，n个 评 价 准 则 ，记 为C={c1,c2,…,cn}，各准则间相互独立，准则的权向量为ω=(ω1,ω2,…,ωn)，有0≤ωj≤1且由于客观世界的不确定性，方案ai(i=1,2,…,m)关于准则cj(j=1,2,…,n)的评价值Xij为随机变量，其概率密度函数未知，我们需要根据有限的样本信息推断相应的总体特征。准则cj(j=1,2,…,n)下的参照点为hj(j=1,2,…,n)，则有如下定义：

定义1方案ai关于准则cj的评价值为连续型随机变量按如下处理方式将连续型随机变量离散化：把区间[uij-3σij,uij+3σij]均匀分为N等份，每等份为Δij=((uij+3σij)-(uij-3σij))/N=6σij/N，zijk=(uij-3σij)+k⋅Δij(K=0,1,…,N)，取值为zijk(k=0,1,2,…,N)的概率为：

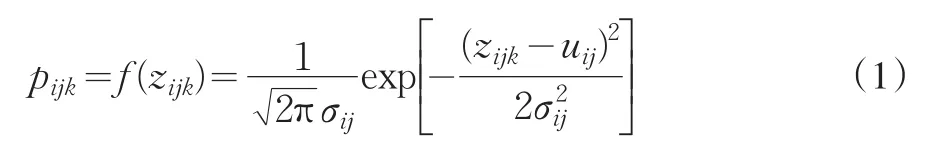
因此，随机变量Xij的取值序列为(zij0,zij1,…,zijN)，相应的概率为(pij0,pij1,…,pijN)。备选方案方案ai(i=1,2,…,m)关于准则cj(j=1,2,…,n)下的前景值：

基于累积前景理论和Bayesian Bootstrap的随机多准则决策方法步骤如下：

步骤1：中心极限定理从数学上证明了受大量相互独立的随机变量综合影响的随机变量往往服从或近似服从正态分布，因此，我们假设备选方案ai(i=1,2,…,m)在准则cj(j=1,2,…,n)下的准则值Xij服从正态分布其中uij和未知。根据Bayesian Bootstrap法，模拟备选方案ai(i=1,2,…,m)在准则cj(j=1,2,…,n)下的准则值Xij的均值uij和方差，进而得到准则值Xij的概率密度函数fij。

步骤2：按式(1)-(7)计算备选方案服从正态分布的方法计算备选方案ai(i=1,2,…,m)在准则cj(j=1,2,…,n)下的前景值vij，得到前景值矩阵V=(vij)m×n

步骤3：将前景矩阵V=(vij)m×n进行规范化处理，得到列和归一化矩阵R=(rij)m×n，其计算公式为：

显然有0＜rij≤1,i=1,2,…,m;j=1,2,…,n。

步骤4：依据规范化矩阵R=(rij)m×n，计算准则cj的熵值Ej：

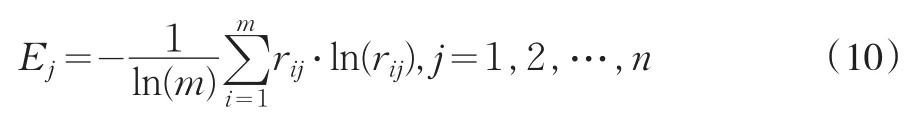
步骤5：依据得出的Ej，计算准则cj的熵权ωj：

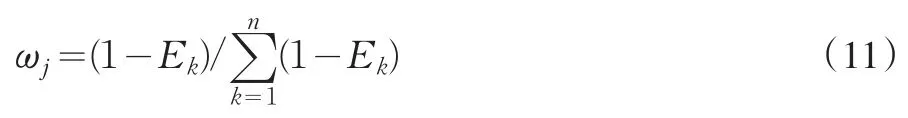
步骤6：按简单加权平均算子计算备选方案ai(i=1,2,…,m)的综合前景值Vi：

按综合前景值对备选方案进行排序和择优。综合前景值V越大，方案越优。

3 算例分析

汽车大修是为了彻底恢复汽车完好技术状况和延长汽车使用寿命而进行的作业，汽车大修可靠性是衡量汽车大修质量的重要指标之一。一般从如下3个方面评价大修汽车的可靠性：c1-平均首次故障里程（MTTF，km），c2-平均故障间隔里程（MTBF，km），c3-故障率（D，次1000km-1）。MTTF是指汽车故障前的平均工作里程，MTEF-是指汽车在两次相邻故障间的平均工作时间，反映了无故障的平均时间。D表示故障的频繁程度。但是在可靠性试验中，多数情况下不能对研究总体进行全数试验，而是从总体中抽取样本进行试验，然后跟据样本试验结果的统计量对总体进行估计。现有4中不同型号的汽车ai(i=1,2,3,4)需要大修，试根据如下测试数据（如表1所示），选出可靠性最高的汽车进行维修。

表1 大修汽车可靠性试验记录

根据上述方法对上述4类汽车进行可靠性评估，具体步骤如下：

（1）假设上述4类汽车在各个指标下的准则值Xij均服从正态分布根据Bayesian Bootstrap方法模拟准则值的经验分布，模拟次数M=5000，模拟结果如表2所示：

表2 备选方案在各准则下的经验分布

（2）根据1991年实施的“汽车产品质量检验方法”（QCn29008.4-91），汽车的MTTF、MTBF和D的参照点分别为2500.0km,1500.0km和5.8次1000km-1，按照第三节步骤2中计算备选方案服从正态分布的方法计算备选方案ai(i=1,2,3,4)在准则cj(j=1,2,3)下的前景值vij，其中，我们采用曾建敏在文献[9]中的建议值，即α=1.21，β=1.02，λ=2.25。前景理论中决策权重函数的参数γ+、γ_和ϕ采用文献[10]的建议值，即γ+=0.8，γ_=0.8，ϕ=1，得到前景值矩阵V=(vij)3×4，如表3所示。

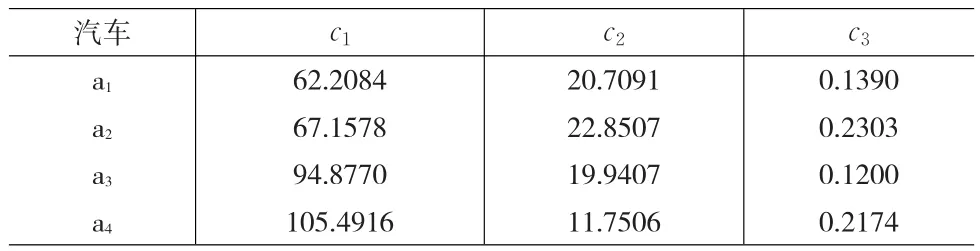
表3 各方案在各准则下的前景值

（3）按公式（8）和（9）对前景矩阵V=(vij)3×4进行规范化处理，得到规范化矩阵R=(rij)3×4：

（4）根据式（10）计算准则cj(j=1,2,3)的 熵 值Ej(j=1,2,3)：

E1=0.5008，E2=0.3968，E3=0.5732

（5）根据式（11）计算准则cj(j=1,2,3)的 熵 权ωj(j=1,2,3)：

ω1=0.3264，ω2=0.3945，ω3=0.2791

（6）按式（12）计算备选方案ai(i=1,2,3,4)的综合前景值Vi，得到V1=28.5134，V2=30.9992，V3=38.8680，V4=39.1287。因此，这4种大修汽车中可靠性最高的是a4，可靠性从高到低的顺序依次为a4≻a3≻a2≻a1。

4 结论

本文研究了准则权重完全未知、准则值部分缺失的多准则决策问题，纳入决策主体的风险偏好，提出了一种基于累积前景理论和随机加权法的信息不完全的多准则决策方法。该方法在考虑决策者风险态度的同时，通过Bayesian Bootstrap模拟准则值的经验分布函数，量化决策信息的不确定性，更科学地为不确定情况下的判断与决策提供指导，降低了决策风险，提高了决策质量。在实际决策过程中，可以根据决策个体的风险偏好特征，适当调整模型参数，以便更合理的辅助行为主体做决策。

[1]郑忠国.随机加权法[J].应用数学学报,1987,(2).

[2]Kahneman D,Tversky A.Prospect Theory:an Analysis of Decision Under Risk[J].Econometrica,1979,47(2).

[3]Tversky A,Kahneman D.Advances in Prospect Theory:Cumulative Representation of Uncertainty[J].Journal of Risk and Uncertainty,1992,5(4).

[4]Lahdelma R,Salminen P.Prospect Theory and Stochastic Multicrite⁃ria Acceptability Analysis[J].Omega,2009,37(5).

[5]王坚强,周玲.基于前景理论的灰色随机多准则决策方法[J].系统工程理论与实践,2010,30(9).

[6]Prelec D.Compound Invariant Weighting Functions in Prospect Theo⁃ry[M].Cambridge:Cambridge University Press,2000.

[7]Efron B.Bootstrap Methods:another Look at the Jackknife[J].The An⁃nals of Statistics,1979,7(1).

[8]陈红.Bootstrap方法及其应用[J].青岛大学学报:工程技术版,1997,12(3).

[9]曾建敏.实验检验累积前景理论[J].暨南大学学报(自然科学版),2007,28(1).

[10]Prelec B D.The Probability Weighting Function[J].Econometrica,1998,66(3).