基于双精度神经网络的RFID企业估值的研究

丁 岚，李树刚

(上海交通大学机械与动力工程学院，上海 201100)

0 引言

物联网被普遍认为将成为2008年全球金融危机之后经济发展新的动力之一，在物联网产业链中，射频识别技术（RFID）在物联网起步阶段就有强大的市场需求，成为了市场最为关注的技术。要想实现成功的投资，正确计算目标企业的价值是关键。估值模型的可靠性不仅取决于总体正确率，也应该考虑各个类别的分类正确率。例如某种模型通过对大量样本的测试验证了它的总体正确率很高，可是对于其中一种少数情况，却完全无法正确估值，而假设这种少数情况恰巧是一种极端风险的情况（如企业利润大幅降低），那么这个模型的可靠性就大打折扣。而目前的估值方法往往缺少对细分情况的考虑，以净现值方法为代表的传统估值方法为例，其中未来自由现金流量的判断就存在着随意性或单一性的缺点。在预测未来现金流时，无论是以回归模型、时间序列分析、灰色系统理论为代表的统计方法，还是以模糊方法，进化算法、神经网络方法等为代表的人工智能方法，都是基于单目标的方法，即只针对模型的总体准确率来优化，这样有可能忽略了某些关键类别的可靠性。本文提出了基于NSGAII优化神经网络的双精度神经网络利润预测模型，准确度和最小分类精度是优化的两个目标，以此来降低估值模型的不确定性和风险性。我们提炼了28个可能影响企业利润的关键因素，把这些因素作为双精度神经网络的输入对企业不同年限的利润进行预测，将预测的利润值代入实物期权模型中进行短期，中期以及长期的估值。通过对中国RFID企业估值的仿真结果表明，改进的神经网络能明显提高实物期权方法估值的准确性。

1 估值系统的设计

1.1 企业估值系统结构

如图1所示，我们设计的一个企业估值系统主要由三个模块组成：评估因素、利润预测和价值评估。

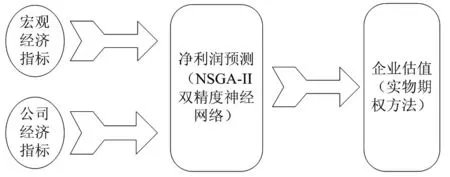
图1 企业估值支持系统结构

在决策模型中，第一步就是建立评估指标体系作为系统的输入。由于估值时需要计算企业在未来投资期内的自由现金流，因此我们将采用基于NSGA-II的双精度神经网络对企业未来的利润进行预测，最后我们选择实物期权的方法来建立企业估值模型，充分考虑了企业的资本价值和投资的机会价值。

1.2 评估因素

在企业估值过程中，对于企业财务状况的分析是最重要的环节，然而仅仅依靠企业财务信息而不考虑宏观经济运行的大方向，很有可能做出危险的预测。因此我们将评估指标分为两类：宏观经济指标和企业财务指标，得到了如图2所示的指标体系，共28个指标。

2 双精度神经网络结构

我们考虑采用最为常用的多层感知器（MLP）神经网络结构，网络有3层：输入层、隐含层、和输出层。此外对输出结果进行处理，得到两个衍生层：未来利润层和企业价值层，如图3所示。

图2 评估指标体系

图3 决策支持系统网络拓扑结构示意图

2.1 双精度进化目标函数

在该网络的进化过程中，我们需要考察两个目标：最小分类精度和总体正确率。我们希望通过NSGA-II进化方法找到能表达正确率和最小分类精度都很高的个体，因此有两个目标函数：

S代表神经网络对于输入样本的最小分类正确精度，表示各个类别分类正确的概率，A代表总体正确率，表示总体样本分类正确的概率。以图4为例，总体样本40个中，甲类有30个，乙类有10个，第一种分类方法，甲类和乙类的样本全部分在了甲类,甲类的正确率是30/30=100%，乙类的正确率是0/10=0，最小的分类精度是min(0,100%),故最小分类精度S=0,总体分类精度A=30/40=75%；第二种分类方法中，甲类中有19个分到了甲类，11个分到了乙类，故甲类的分类正确率为19/30=63.3%，同理，乙类的分类正确率是3/10=30%，故S=min(63.3%,30%)=30%，总体的正确率A=(19+3)/40=55%，

从图4中我们也可以看出，A和S的变化并没有表现出一致性，这两个目标函数不存在明确的相关性，有时候还体现出相互冲突性，因此传统的多目标转化为单目标的方法无法有效使用。

2.2 输入层：数据预处理

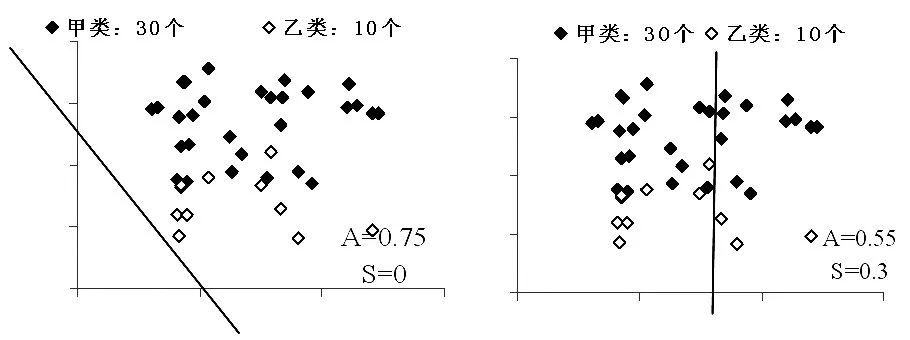
图4 正确率和最小分类精度的示意图

由于在我们的指标体系中，包含了28个指标，如果不加处理全部作为神经网络的输入，比如会是网络结构十分复杂，而且网络中的神经元均采用S型激励函数,对于输入样本数据进行预处理变换后可防止因净输入的绝对值过大而使神经元输出饱和，继而使权值调整进入误差曲面的平坦区。

对于维度太多的问题，我们采用主成分分析的方法来降维处理，主成分分析就是把原有的多个指标转化成少数几个代表性较好的综合指标，这少数几个指标能够反映原来指标大部分的信息，并且各个指标之间保持独立，避免出现重叠信息，起着降维和简化数据结构的作用。通过主成分分析，保留98%的信息，输入的数据变成由28个变成10个，降维效果很显著。

接着，为了防止数据的过度不均匀，我们对这些数据进行归一化处理，归一化公式为：

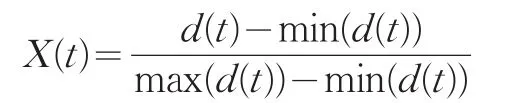
2.3 隐含层和输出层

设网络有N个输入节点，H个隐含层节点，M个输出层节点，隐含层节点采用S型函数，每个隐含层节点的输出为：

其中βh表示隐层节点上的偏置，WIH代表输入层与隐含层之间的连接矩阵，X表示输入的指标矩阵。输出层首先按加权求和得到一个输出fm：

其中γm表示输出节点上的偏置，WHO代表隐含层与输出层之间的连接矩阵，V代表隐含层的输出矩阵。

再采用softmax函数计算样本落入第m类的概率om，为节点的输出：

最后样本所在的类C(X)为输出最大的节点所代表的类：

2.4 价值评估层：实物期权方法

我们将前一层输出的结果表达为未来的利润，为实物期权法计算企业价值时提供必要的参数。

从实物期权的角度出发，企业的价值评估应该包括两个部分：资产价值和期权价值:

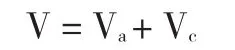
Va：贴现现金流(DCF)方法得到的现实资产的折现值，即资产的价值。

Vc：是未来增长机会的折现值，即期权的价值。

采用自由现金流量折现法计算目标企业的资产价值时，

其中：

Ci—第i年的净利润；

r—无风险利率；

S—企业目前的价值。

在我们运用实物期权原理时评估一个企业的价值时，期权价值可以看作我们拥有了在投资末期出售以更比投资初期更高价值出售这个企业的选择权，因此我们可以采用因此Black-Scholes看涨期权模型（简称BS模型），S是这个企业目前的价值，X是投资末期企业的价值。

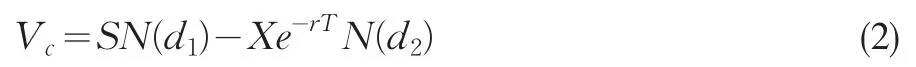
其中：

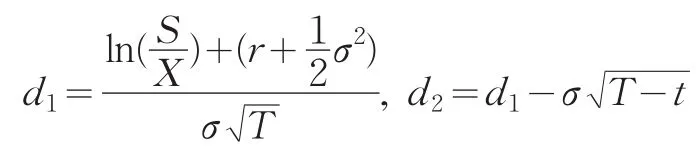
参数代表的意义和确定方法见表1。

表1 BS公式中各参数的含义和确定方法

以上可以发现，神经网络对未来净利润情况的预测能帮助我们确定DCF方法中的Ci和BS公式中的X，假设企业的净利润全部累积，有：

综合得到企业的估值公式为：

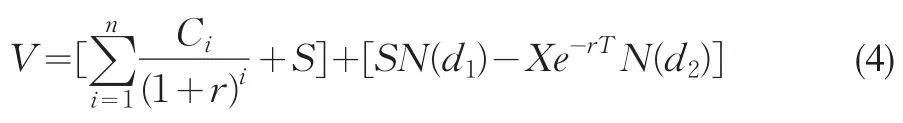
3 NSGA-II多目标进化算法

NSGAⅡ是带精英策略的非支配排序遗传算法，它是Deb等人在NSGA的基础上加入快速非支配排序算法、引入精英策略、采用拥挤度和拥挤度比较算子，使得Pareto最优解前沿中的个体能均匀地扩展到整个Pareto域，保证了种群的多样性。NSGA-II算法的基本思想为：首先，随机产生规模为的初始种群，非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；其次，从第二代开始，将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；最后，通过遗传算法的基本操作产生新的子代种群；依此类推，直到满足程序结束的条件。

3.1 快速非支配排序和拥挤度算子

在快速非支配排序过程中值越小排名越优先，故实际上考虑的是：

f1=-A和f2=-S，

假设种群 P，对于 x，y∈ P，若 f1(x)≤ f1(y)且 f2(x)＜ f2(y)，或f1(x)＜ f1(y)且 f2(x)≤ f2(y)，则称 x支配y。对于每个个体p都有两个参数np和Sp,其中np为种群中支配个体p的个体数，Sp为种群中被个体p支配的个体集合。算法的

主要步骤是:

步骤1找到种群中所有np=0的个体,并保存在当前集合F1中，故集合F1中的个体没有被任何其他的个体支配，是Pareto最优边界；

步骤2对当前集合F1中的每个个体p,其所支配的个体集合为Sp,遍历Sp中的每个个体p,执行np=np-1,如果np=0,则将个体p保存到集合Q中，故集合Q中的个体仅被集合F1中的个体支配，不被任何F1和Q集合外的个体支配，Q为集合F2；

步骤3重复上述操作,直到整个种群被分级。

一旦非支配集排序完成后，我们就要计算拥挤度。拥挤度是指种群中给定个体的周围个体的密度。直观上可表示为个体i周围仅包含个体i本身的长方形的边长的和。如图5所示。

图5 拥挤度示意图

对于双目标排序问题，拥挤度确定方法是:

Fi中的每个个体,边界的两个个体拥挤度为无穷，即：

I(d1)=I(dn)=∞

则对于其他个体利用差值法对每个目标函数进行拥挤度计算:

其中f(i±1）m表示集合中从第m维来看，与第i个个体的最相邻的个体的目标函数m的值，分别为目标函数m的最大最小值（m=1,2）。

这样,通过快速非支配排序以及拥挤度计算,种群中的每个个体i都有两个属性:非支配排序和拥挤度。利用这两个属性,可以区分种群中任意两个个体的支配和非支配关系,也就是说:如果两个个体的非支配排序不同，取排序号较小的个体(分层排序时，先被分离出来的个体)；如果两个个体在同一级，取周围较不拥挤的个体。

3.2 染色体编码和初始化

由于每一个染色体代表着一个参数和结构都具体的神经网络，包括权值和偏置的大小、隐含层节点数目，连接情况等，因此染色的编码可以视为三段。如图6所示，第一段为参数部分的编码，表示所有权值和偏置的大小，初始化时，输入层与隐含层之间的参数在[-5,5]之间随机产生，隐含层和输出层之间的参数在[-10,10]之间随机产生；第二段为隐层节点的编码，“0”表示该位置节点不存在，“1”代表存在，这一段的编码在初始化时随机生成“0”或“1”，但“1”的个数在最小和最大节点数之间，我们设定最小节点数为3，最大节点数可以在实验中灵活设置；第三位表示连接情况，“0”表示该位置没有连接，“1”表示有连接，同样初始化时每个编码随机生成“0”或“1”，并保证隐含层有节点的位置与前后层的连接不能全为0。

图6 染色体编码示意图

3.3 突变

进化过程中的基因算子只考虑了突变没有考虑交叉，因为已有文献表明交叉操作在遗传进化过程不能帮助优化神经网络。我们考虑了五种突变的情况，一种参数突变和四种结构突变，发生的概率均为1/5，如表2所示。

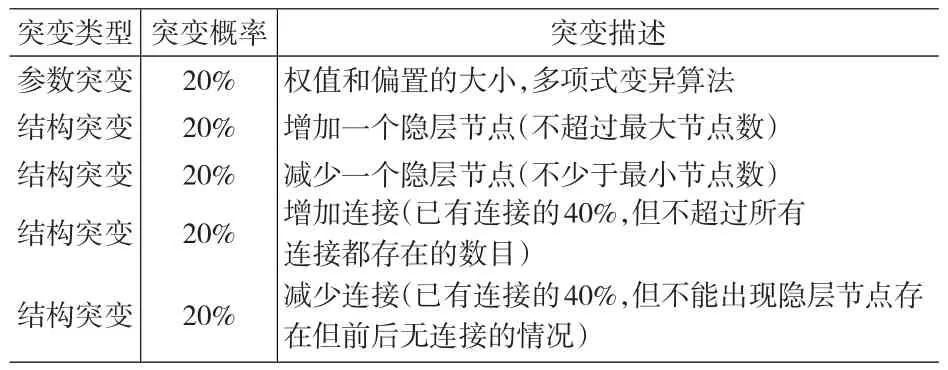
表2 五种突变操作

3.4 算法设计

在我们基于NSGA-II算法优化神经网络的研究中，学习算法可以设计如下：

（1）产生初始种群，染色体表示一个神经网络的权值和偏置（实值）、连接和隐层节点个数（0/1）。

（2）评价初始种群，将种群中的染色体翻译成神经网络，计算准确率和最小分类精度。

（3）快速非支配排序法给种群排序，每个染色体得到一个排名和拥挤距离。

（4）通过锦标赛方法来挑选父代，对父代的每个个体进行突变操作，以各1/5概率发生一种参数突变四种结构突变（加/减隐层节点，加/减连接数），产生子代。

（5）评价子代，计算准确率和最小分类精度。

（6）将子代父代合并在一起用快速非支配排序法计算排名和拥挤度，截去多余的个体，保持种群数量恒定。

（7）检查是否达到终止条件，如没有则转入步骤4，用新种群替代就旧种群。

从以上步骤可以看出，采用NSGA-II优化神经网络，能得到参数、结构更合适的个体，他们在正确率和最小分类精度上都得到了提高，算法的程序框图如图7所示。

图7 双精度神经网络算法程序框图

4 结论

在投资者对于RFID企业进行投资时如并购、投融资、交易等，至关重要的一步就是对企业有一个可靠的价值评估，从而分析和衡量企业的公平市场价值并提供有关信息，便于投资者和管理者做出建议与决策。但是传统的现金流预测模型没有考虑到细分情况下的精度优化，且传统估值方法忽略了投资机会选择的价值，因此估值的效果受到了影响。为此本文设计了一个集成双精度神经网络与实物期权估值方法相结合的估值系统。与现有文献相比，该系统的主要特色体现在：

（1）双精度神经网络在训练神经网络时，以准确度和最小分类精度为进化的目标，基于Pareto边界法，同时对准确度和最小分类精度这两个目标进行优化，强化了模型的抗风险性。

（2）采用实物期权方法，克服了传统净现值方法忽略对未来投资机会价值的缺点。

（3）在进化过程中，网络的参数和结构同时参与到变异操作中，传统神经网络对于隐层节点数的确定没有明确的规则，在双精度神经网络中，变异算子对每个父代个体均等的发生参数突变和结构突变，最后神经网络在隐层节点、节点间的连接等结构设计上得到了优化。

未来的研究主要是对输出结果的进一步优化上，本文主要是搭建了一个分类预测模型，只能给投资者一个定性的决策支持，还缺乏连续量化的手段。其次，对于已有的分类结果，仍需进一步提高精度，在实验对比中，多值Logistic回归模型的表现也比较优秀，未来希望吸收各种预测手段的优势设计出一个更可靠的综合神经网络。

[1]中国商业电讯.物联网风生水起将成下一风投热点[EB、OL].http://www.prnews.cn/press_release/33424.htm，2010-03-30.

[2]冯文权.经济预测与决策技术[M].武汉：武汉大学出版社,2008.

[3]汉克,维歇恩.商业预测[M].北京：清华大学出版社,2006.

[4]庞素琳.信用评价与股市预测模型研究及应用—统计学、神经网络与支持向量机方法[M].科学出版社,2005.

[6]马明,李松.基于遗传算法优化混沌神经网络的股票指数预测[J].商业研究,2010(11).

[7]张鸿,彦林辉.应用混合神经网络和遗传算法的期权价格预测模型[J].管理工程学报,2009,(1).

[8]Y.Jin,B.Sendhoff.Pareto-Based Multi Objective Machine Learning:An Overview and Case Studies[J].IEEE Trans.Syst.Man Cybern.C,Appl.Rev.,2008,38(3).

[9]Deb,Kalyanmoy,Pratap,Amrit,Agarwal,Sameer,Meyarivan,T.A Fastand ElitistMulti-ObjectiveGenetic Algorithm NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2).

[10]P.J.Angeline,G.M.Saunders,J.B.Pollack.An Evolutionary Algo⁃rithm that Constructs Recurrent Neural Networks[J].IEEE Trans.Neural Netw.,1994,5(1).